Kurvor

Förutom grafen till en funktion kan GeoGebra också användas till att göra en kurva som är

• definierad av en ekvation i \(x\) och \(y\),
• den geometriska orten av en punkt som uppfyller något villkor,
• en parametrisk kurva.

Ladda GeoGebra-arbetsblad

Implicita funktioner

GeoGebra skiljer på explicita funktioner och funktioner som är implicit definierade av ekvationer i \(x\) och \(y\).

En explicit funktion skrivs med hjälp av parenteser ‐ med \(f(x)\)-notation.

En implicit funktion kan exempelvis skrivas som \(y=x^2\). I detta fall kan \(y\) uttryckas explicit som ett uttryck av \(x\) och den kurva som visas hade också kunnat visas som grafen till funktionen \(f(x) = x^2\). En implicit funktion kan dock ha flera \(y\)-värden till ett \(x\)-värde, och är därför ett mer generellt begrepp än en funktion. En ekvation beskriver en relation mellan \(x\) och \(y\), och det är inte alltid så att \(y\) explicit kan formuleras med hjälp av \(x\). Ekvationen \(x^2+y^2=1\) definierar en kurva som är enhetscirkeln. Alla punkter \((x, y)\) som satisfierar ekvationen ligger på enhetscirkeln. Kurvan är implicit definierad av ekvationen.

GeoGebra kategoriserar en kurva till en implicit funktion som en Linje, ett Kägelsnitt, eller en Implicit kurva.

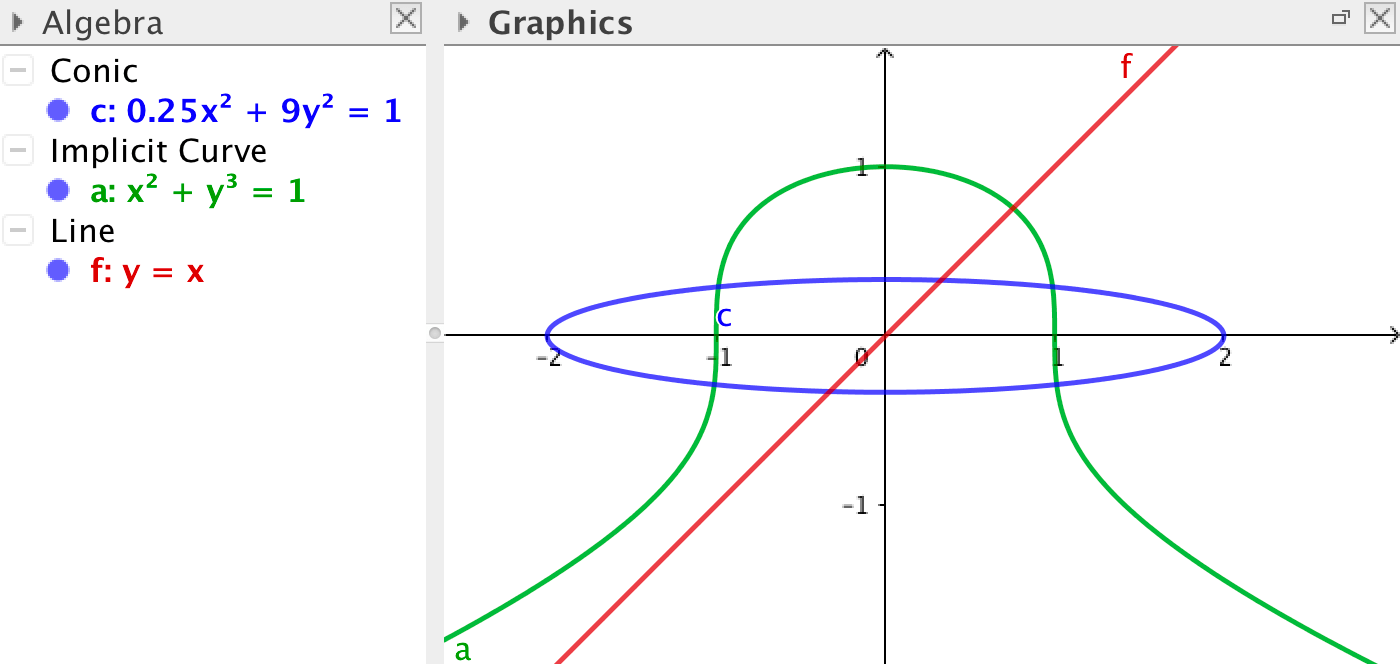
GeoGebra kan skapa implicita kurvor som är definierade av ekvationer, om ekvationerna innehåller polynom i \(x\) och \(y\). Om du exempelvis skriver in ekvationen y = sin(x) kommer GeoGebra att klassificera detta som en funktion, en funktion som får ett namn av GeoGebra.

Kommandon som tar en funktion som argument, fungerar inte på kägelsnitt och linjer. Om a är definierat av ekvationen y=x^2, kan du inte använda kommandot Extrempunkt på a. Om du vill använda kommandon för funktioner, måste funktionen skrivas in som en funktion, dvs med \(f(x)\)-notation!

Geometrisk ort

Om du har en punkt som uppfyller något villkor så är mängden av alla sådana punkter en geometrisk ort.

För att göra en geometrisk ort i GeoGebra behöver du en punkt \(B\) som antingen beror på en annan punkt \(A\) eller en glidare. Punkten \(A\) måste ligga på någon kurva eller en koordinataxel. Med verktyget Geometrisk ort kan du nu skapa den geometriska orten genom att först klicka på \(B\) och sedan på \(A\) eller på glidaren.

Polära koordinater

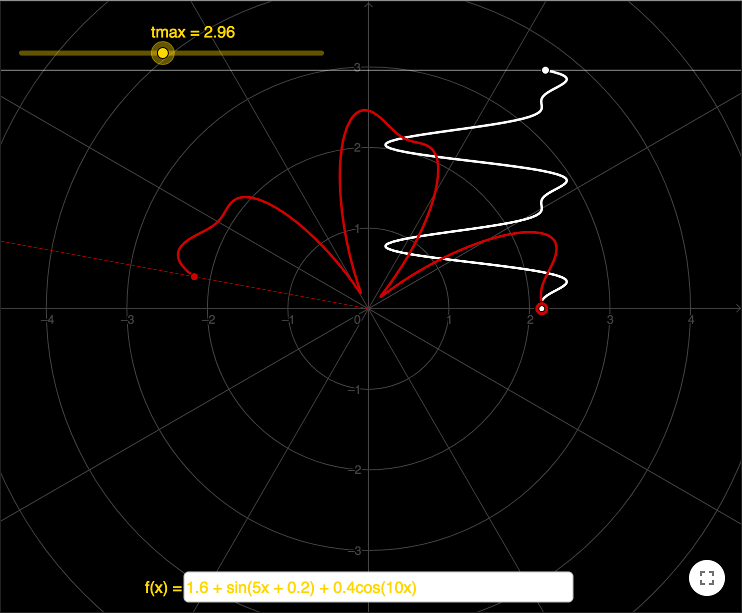
I GeoGebra kan man använda polära koordinater då man definierar en punkt. Då man använder polära koordinater, används semikolon som skiljetecken, exempelvis som A=(r;α). Genom att låta vinkeln få sitt värde från en glidare \(t\), och genom att definiera en funktion \(r(x)\), kan man få fram den kurva som punkten A=(r(t);t) genomlöper. Använd verktyget Geometrisk ort, klicka på punkten och sedan på glidaren. Under Inställningar för Ritområde, under tabben Grid, kan du ändra rutnätet till polär form.

Polära koordinater kan skrivas som kartesiska koordinater genom att låta \(x=r\cos(t)\) och \(y=r\sin(t)\). Detta kan användas för att rita kurvan som en parametrisk kurva istället för en geometrisk ort.

Parametriska kurvor

Om \(x\)- och \(y\)-koordinaterna båda beror på en variabel \(t\), beskriver de en parametrisk kurva med parametern \(t\). Varje punkt på kurvan beskrivs av koordinaterna \((x(t),y(t))\). Genom att låta \(t\) variera mellan värdena \(start\) och \(stopp\) kan du rita kurvan \(k\) genom att skriva in

k = Kurva( x(t), y(t), t, start, stop)

i inmatningsfältet.

Du kan alltid göra om en vanlig funktion till en parametrisk funktion. Exempelvis kan du rita grafen till funktionen \(f(x)=x^2,-10\leq x \leq 10\) genom att skriva in koden:

k = Kurva(t, t^2, t, -10, 10)

Genom att låta en glidare representera stopp-värdet, kan man visualisera hur en graf ritas upp. Skapa en glidare tmax och definiera kurvan som:

k = Kurva(t, t^2, t, -10, tmax)

Transformationer och kurvor

Den enda transformation du kan använda på grafen till en vanlig funktion är Parallellförflytta objekt med vektor.

En parametrisk kurva kan du, förutom att parallellförflytta, också transformera genom att använda verktyget Spegla objekt i en linje eller verktyget Rotera objekt runt punkt med vinkel.

Övningar

Övning 1

Gör kägelsnitt

Skapa fyra glidare \(a\), \(b\), \(h\) och \(k\).

Inom analytisk geometri kan en parabel definieras av ekvationen

en ellips av ekvationen

och en hyperbel av ekvationen

Skapa de tre kägelsnitten med hjälp av dessa ekvationer.

Hur påverkar värdena av \(h\) och \(k\) de tre kurvornas utseende?

Hur påverkar värdena av \(a\) och \(b\) ellipsens och hyperbelns utseende?

Övning 2

Solen, jorden och månen

Skapa en glidare \(R\) som representerar den radie jordens bana runt solen har.

Skapa en glidare \(r\) som representerar den radie månens bana runt jorden har.

Skapa en heltalsglidare \(m\) som representerar hur många månader det går på ett år.

Placera en punkt \(S\) (solen) i origo.

Version 1 ‐ med grader och rotationer

Skapa en vinkel-glidare \(\alpha\) som representerar den vinkel jorden har.

Placera en punkt \(J\) (jorden) på den positiva \(x\)-axeln. Avståndet mellan \(S\) och \(J\) ska vara \(R\). Använd verktyget Rotera objekt runt punkt med vinkel för att rotera \(J\) runt \(S\) med vinkeln \(\alpha\). Den roterade punkten kommer att kallas \(J'\). Göm punkten \(J\).

Gör en punkt \(M\) (månen) genom att skriva in M = J'+(r, 0). Nu ska \(M\) roteras runt \(J'\) med en vinkel som beror på antalet månader \(m\) och på vinkeln \(\alpha\). Bestäm denna vinkel och skapa den roterade punkten \(M'\). Göm punkten \(M\).

Använd verktyget Geometrisk ort. Klicka först på \(M'\) och sedan på glidaren \(\alpha\).

Version 2 ‐ med radianer och trigonometri

Skapa en glidare \(a\) med värden mellan \(0\) och \(2\pi\) som representerar den vinkel jorden har.

Låt punkten \(J\) representera jorden. Bestäm \(x\)- och \(y\)-koordinat för \(J\) uttryckt med hjälp av lämpliga glidare. Skriv in dessa värden för punkten i inmatningsfältet.

Låt punkten \(M\) representera månen. Bestäm \(x\)- och \(y\)-koordinat för \(M\) uttryckt med hjälp av lämpliga glidare. Skriv in dessa värden för punkten i inmatningsfältet.

De uttryck som används för månens koordinater fungerar även till att göra en parametrisk kurva som visar månens bana. Skapa denna kurva. Du kan anta att parametern har startvärdet \(0\) och slutvärdet \(a\).

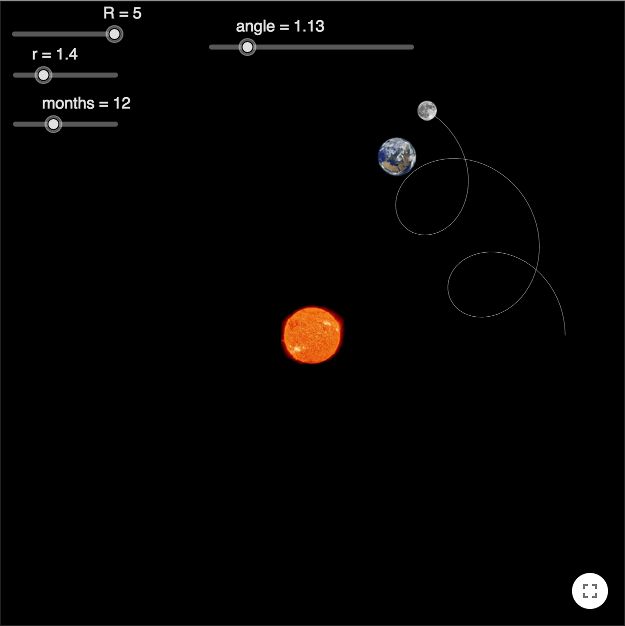
Kommentar: Det går att visa bilder istället för punkter. Bilderna i arbetsbladet nedan är hämtade från NASAs bildgalleri.

Ladda GeoGebra-arbetsblad

Den kurva som ritas upp av månen är en så kallad epitrokoid.

Övning 3

Värdemängd och definitionsmängd till inversa trigonometriska funktioner

Om \(f^{-1}\) är den inversa funktionen till en funktion \(f\), så är grafen till \(f^{-1}\) speglingen av grafen till \(f\) i linjen \(y = x\).

För att kunna spegla grafen till en funktion, måste den definieras som en parametrisk kurva.

• Definiera funktionen f(x) = sin(x). Göm grafen.

• Lägg två punkter \(A\) och \(B\) på \(x\)-axeln. Punkterna representerar intervallgränserna till funktionens begränsade definitionsmängd.

  Du kan visa en punkts \(x\)- eller \(y\)-koordinat som etikett till punkten. Skriv in %x eller %y som Förklaring till objektet i egenskapsfönstret.

• Gör en parametrisk kurva till funktionen \(f(x)= \sin(x), x(A) \le x \le x(B)\).

• Spegla kurvan i linjen \(y=x\). Du kan antingen använda verktyget Spegla objekt i en linje eller kommandot Spegla( <Objekt>, <Linje> ).

• Länka \(f\) till en inmatningsruta med verktyget Inmatningsruta så att du lätt kan definiera om funktionen.

• Dra i punkterna. Studera vilka intervall som gör att den speglade grafen hade kunnat vara grafen till en funktion. Vad blir i sådana fall värdemängd respektive definitionsmängd för den inversa funktionen?

Övning 4

Gör en Lissajous-kurva

En Lissajous-kurva uppkommer av en periodisk rörelse längs \(x\)-axeln och en längs \(y\)-axeln.

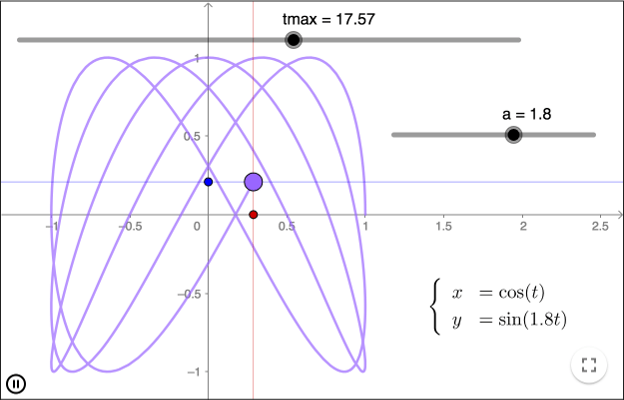
En Lissajous-kurva kan beskrivas av en parametrisk ekvation

En enklare ekvation visas i arbetsbladet nedan.

Ladda GeoGebra-arbetsblad

Visualisera en Lissajous-kurva så att de två periodiska rörelserna längs koordinataxlarna också visas.

Man kan också göra dämpade Lissajous-kurvor, se Damped Lissajous Curves för mer information.