Vektorer och matriser
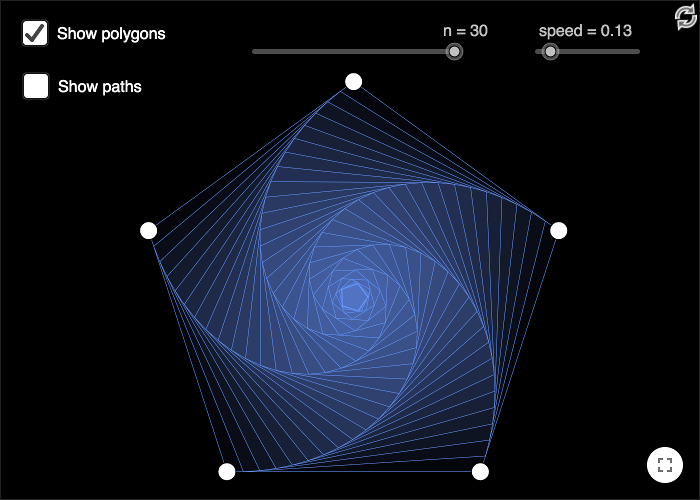
Förflyttningarna är skapade med vektorer.
Vektorer
En vektor har en längd och en riktning. I GeoGebra gör du en vektor antingen genom att använda verktyget eller genom att skriva ett kommando i inmatningsraden.
Se Lär dig GeoGebra - Punkter och vektorer för information om hur GeoGebra skiljer mellan punkter och vektorer. Vektorer används ofta för att parallellförflytta objekt.
Enhetsvektorer
Enhetsvektorer är vektorer som har längden en enhet. I GeoGebra gör du en enhetsvektor med hjälp av kommandot
Enhetsvektor[< vektor > ]
I det översta arbetsbladet, jagar myrorna varandra. Längden av varje förflyttning ges av glidaren \(speed\). Om \(A1\) och \(B1\) representerar den första och den andra myrans respektive position, så får man nästa position för den första myran med hjälp av koden:
A2 = A1+speed*Enhetsvektor[Vektor[A1,B1]]
Det enklaste sättet att modellera myror som jagar varandra i GeoGebra, är att använda kalkylbladet.
Translationer längs två vektorer
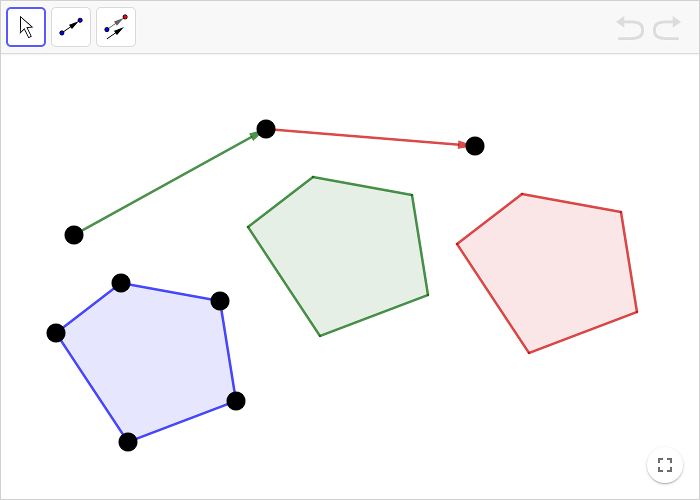
Den blå polygonen translateras först längs den gröna vektorn, resultatet är den gröna polygonen. Sedan translateras den gröna polygonen längs den röda vektorn, resultatet är den röda polygonen.
Gör en ny vektor i appleten ovan.
Translatera den blå polygonen längs den nygjorda vektorn.
Hur skall din nya vektor skapas för att resultatet av din translation alltid skall överlappa den röda polygonen?
Om du lyckas med uppgiften har du åstadkommit en translation som ger samma resultat som två translationer. Detta ger oss ett rimligt sätt att definiera vektoraddition.
Vektoraddition
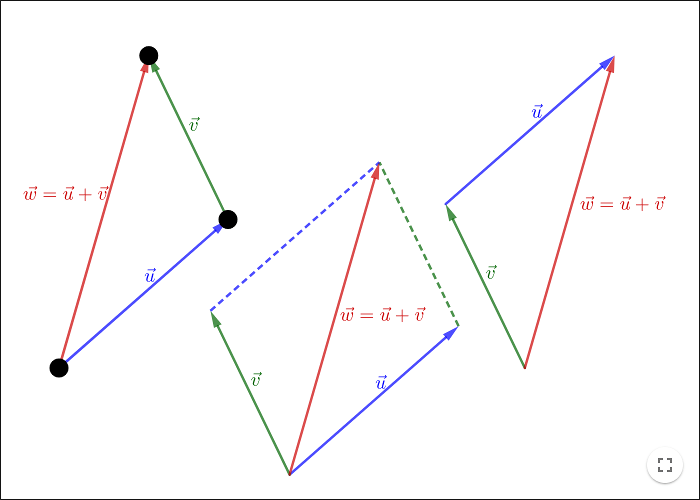
Vektoraddition definieras på följande sätt:
Från konstruktionen ovan ser man att \(\vec{w}=\vec{u}+\vec{v}=\vec{v}+\vec{u}\); det spelar alltså ingen roll i vilken ordning man adderar vektorerna; man säger att vektoraddition kommuterar.
Man kan också representera vektoraddition grafiskt som en parallellogram.
Bas och koordinater
En skalär är ett reellt tal (tills vidare). När man håller på med vektorer behöver man kunna skilja på kvantiteter som har riktning, och kvantiteter som saknar riktning.
Uppgift - Multiplikation med en skalär
Gör en vektor \(\vec{u}\) som utgår från origo.
Skriv in
2*ui inmatningsraden.Skriv in
-ui inmatningsraden.Ändra på vektorn \(\vec{u}\).
Gör en glidare \(a\). Skriv in
a*ui inmatningsraden. Beskriv vad som händer då en vektor multipliceras med en skalär; en positiv eller negativ skalär.
Vad händer då man multiplicerar med noll? Är resultatet en vektor? Vore det rimligt att kalla "nollvektorn" för en vektor eller ej? Om nollvektorn är en vektor på vilket vis skiljer den sig då från andra vektorer?
Några definitioner
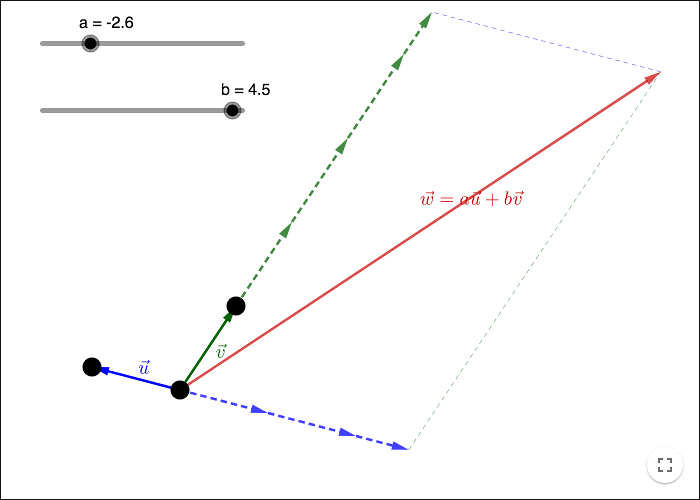
Två icke-parallella vektorer, varav ingen är en nollvektor, kan utgöra en bas för planet. Givet en bas kan en godtycklig vektor skrivas som en linjärkombination av basvektorerna.
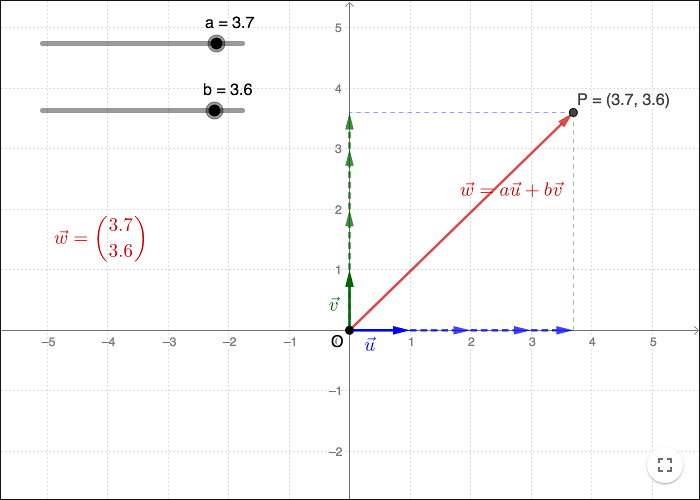
Om basvektorerna kallas \(\vec{u}\) och \(\vec{v}\), kan en godtycklig vektor \(\vec{w}\) skrivas som
\[\vec{w}=a\vec{u}+b\vec{v}\]
för några skalärer \(a\) och \(b\). \(\vec{w}\) är en så kallad linjärkombination av \(\vec{u}\) och \(\vec{v}\). De två skalärerna \(a\) och \(b\) kallas för koordinaterna för vektorn \(\vec{w}\) i basen \(\vec{u}\) och \(\vec{v}\).
Om basvektorerna är givna finns det förenklade sätt att skriva vektorn på, antingen som
\[\vec{w}=(a,b) \hspace{1cm} \text{eller} \hspace{1cm} \vec{w}=\binom{a}{b}\]
Om man har två vektorer \(\vec{w}=a\vec{u}+b\vec{v}\) och \(\vec{z}=c\vec{u}+d\vec{v}\), kan man addera dem på följande vis:
\[\binom{a}{b}+\binom{c}{d}=a\vec{u}+b\vec{v}+c\vec{u}+d\vec{v}=(a+c)\vec{u}+(b+d)\vec{v}=\binom{a+c}{b+d}\]
I GeoGebra används det underliggande koordinatsystemet för att definiera de två basvektorerna. Den första basvektorn är en vektor som börjar i origo och pekar på punkten (1,0), den andra basvektorn pekar på (0,1). En bas för vilken varje basvektor är en enhetsvektor, och där basvektorerna är ömsesidigt ortogonala (vinkelräta mot varandra), kallas för en ortonormerad bas eller ON-bas.
Ortsvektorer
Om man har två punkter i koordinatplanet, kan man göra en vektor mellan punkterna. Genom att välja basvektorerna så att de utgår från origo och pekar på koordinaterna (1, 0) respektive (0, 1), får man en behändig bas om man vill jämföra vektorns koordinater med punkternas koordinater.
Om \(\vec{w}\) pekar på punkten \(P\), så är koordinaterna till vektorn \(\vec{w}\) samma som koordinaterna till punkten \(P\).
\(\vec{w}\) är en vektor som utgår från punkten \(O\) och pekar på punkten \(P\), där \(O\) är origo.
\[\vec{w}=\vec{OP}\]
\(\vec{OP}\) är en så kallad ortsvektor; den är en vektor mellan punkterna \(O\) och \(P\) och kan därför inte flyttas. Vill man ha en flyttbar vektor, introducerar man en vektor \(\vec{w}\) och låter \(\vec{w}=\vec{OP}\).
Genom upprepad vektoraddition finner man att \(\vec{z}=\vec{u}+\vec{v}+\vec{w}\); eller uttryckt i ortsvektorer
\[\vec{OC}=\vec{OA}+\vec{AB}+\vec{BC}\]
Vektorsubtraktion
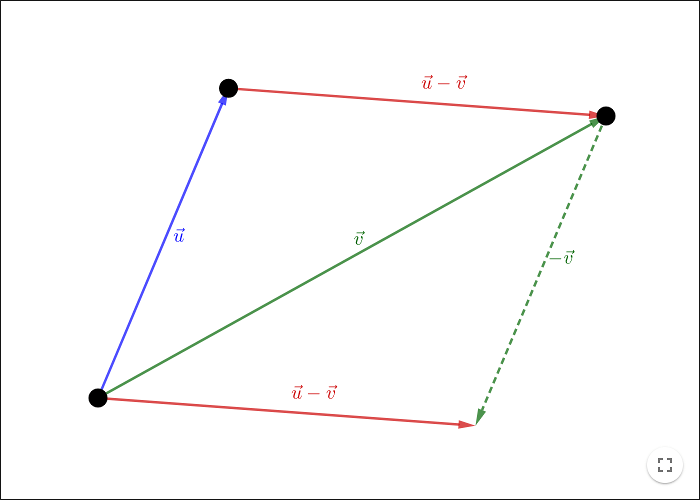
Då två vektorer \(\vec{u}\) och \(\vec{v}\) subtraheras, får man resultat, vektorn \(\vec{u}-\vec{v}\), genom att gå från spetsen på \(\vec{v}\) till spetsen på \(\vec{v}\). Se konstruktionen nedan!
Detta resultat är speciellt användbart då man försöker bestämma koordinaterna för en vektor som ligger mellan två punkter i ett koordinatplan.
Om vektorn \(\vec{PQ}\) ligger mellan punkterna \(P\) och \(Q\) med kända koordinater; kan man bestämma koordinaterna för \(\vec{PQ}\) genom att använda vektorsubtraktion.
Eftersom \(\vec{OP}\) och \(\vec{OQ}\) har samma koordinater som punkterna \(P\) och \(Q\), kan man bestämma koordinaterna för \(\vec{PQ}\) med hjälp av:
\[\vec{PQ}=\vec{OQ}-\vec{OP}\]
Linjens ekvation
En linjes ekvation kan skrivas på parametrisk form med hjälp av vektorer.
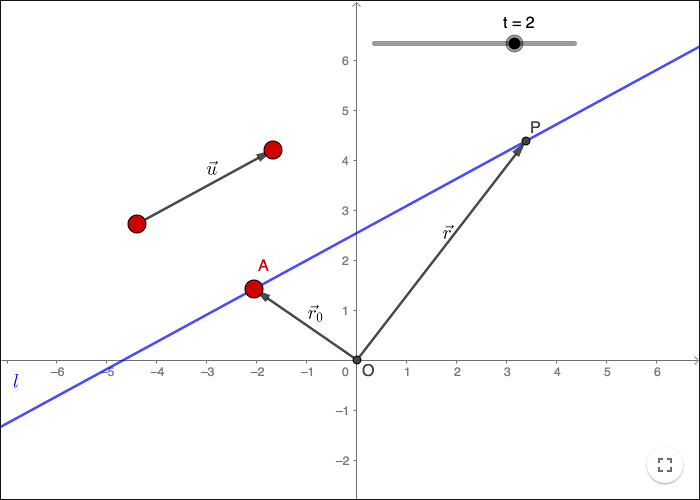
Låt \(l\) vara en linje genom en punkt \(A\) längs en vektor \(\vec{u}\). För varje punkt \(P\) på linjen, gäller ekvationen
\[\vec{OP} = \vec{OA}+t\vec{u}\]för något \(t \in \mathbb{R}\).
Låt \(\vec{r_0}= \vec{OA}\) och \(\vec{r}= \vec{OP}\), linjens ekvation kan skrivas på vektorform som
\[\vec{r} = \vec{r_0}+t\vec{u}.\]Matriser
Om du vill göra matriser i GeoGebra är det enklast att använda kalkylbladet. Matrisen
\[\mathbf{A}=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{array} \right)\]
skrivs in som i bilden nedan. Därefter markerar du de sex cellerna och väljer kalkylbladsverktyget "Skapa matris".
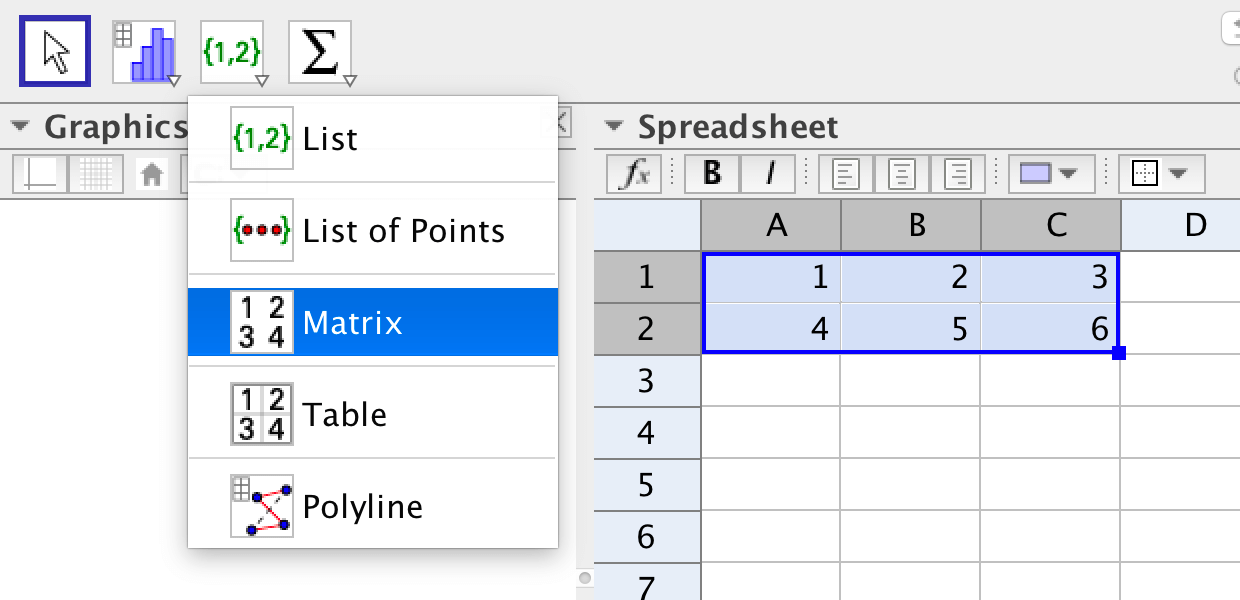
I fönstret som dyker upp kan du namnge matrisen innan du trycker på Create.
Om du klickar på den lilla pilen bredvid inmatningsraden, kan du se alla de kommandon som finns för matriser och vektorer.
Du kan exempelvis skapa en annan matris som är transponatet till \(\mathbf{A}\) med kommandot
Transpose(A)
Transponatet \(\mathbf{A^T}\) till en matris \(\mathbf{A}\), får man genom att låta kolonnerna och raderna byta plats.
\[\mathbf{A^T}=\left( \begin{array}{ccc} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{array} \right)\]
Vill du komma åt ett matriselement använder du kommandot
Element[<matris>, <rad>, <kolonn>]
Exempelvis returneras 6 om du skriver in Element[A,2,3].
Punkter/vektorer och matriser i GeoGebra
En vektor kan ses som en matris med en kolumn, en \(m\times 1\). Vektorn \(\mathbf{u}\) nedan är en \(2\times 1\) matris.
\[\mathbf{u}=\left( \begin{array}{ccc} a \\ b \\ \end{array} \right)\]
Trots de olika sätten att representera punkter och vektorer/matriser, kan man multiplicera en matris med en punkt.
Linjära avbildningar
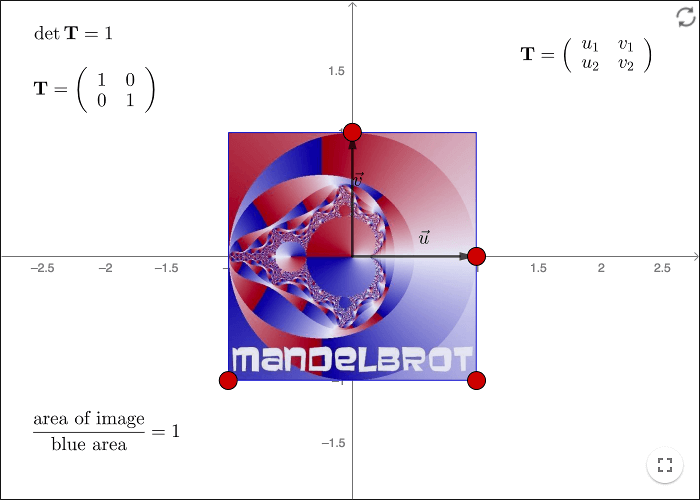
Antag att enhetsvektorerna \(\mathbf{e_1}\) och \(\mathbf{e_2}\) avbildas på vektorerna \(\mathbf{u}=\binom{a}{b}\) respektive \(\mathbf{v}=\binom{c}{d}\). Avbildningsmatrisen blir då
\[\mathbf{T}=\left( \begin{array}{} a & c \\ b & d \\ \end{array} \right)\]
Determinantens absolutvärde ger oss areornas skalfaktor. Betrakta den transformerade bilden av Mandelbrotmängden då determinanten är negativ!
För att visualisera en linjär avbildning av en polygon i GeoGebra, gör så här:
Gör två vektorer \(\mathbf{u}\) och \(\mathbf{v}\) utgående från origo. Placera inte slutpunkterna på x- eller y-axeln, då fastnar de där. Låt slutpunkten till \(\mathbf{u}\) heta \(A\), och slutpunkten till \(\mathbf{v}\) heta \(B\).
Skapa avbildningsmatrisen \(\mathbf{T}=\left( \begin{array}{} x(A) & x(B) \\ y(A) & y(B) \\ \end{array} \right)\).
Lägg in determinanten i en variabel:
detT=determinant[T].Gör en valfri polygon, \(poly1\).
Avbilda polygonen med kommandot
ApplyMatrix[T,poly1].Gör en variabel:
areor=poly1'/poly1.Högerklicka på \(poly1'\), välj Egenskaper och sedan Avancerat. Fyll i
detT>0i fältet ”Blå”, ochdetT<=0i fältet ”Röd”. Polygonen kommer då att bli rödfärgad då determinanten är negativ.Studera variablerna \(areor\), \(detT\) och polygonens färger!
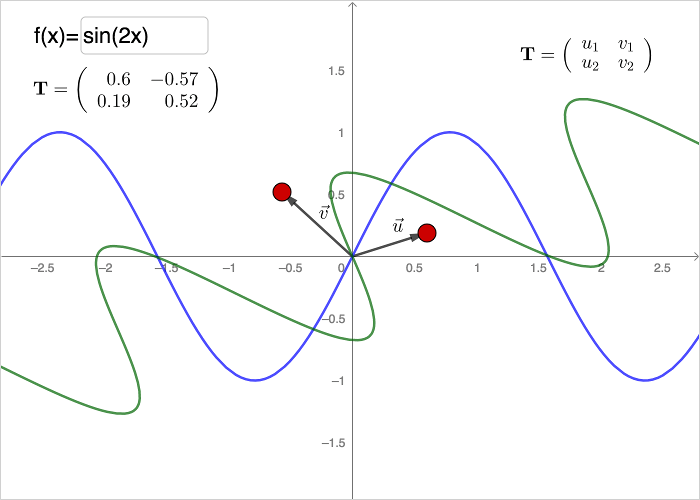
Linjära transformationer av kurvor
Den blå grafen, i arbetsbladet nedan, transformeras till den gröna grafen av matrisen \(\mathbf{T}\).
Grafen till funktionen \(f(x)\) kan ritas som kurvan \(c\) med koden:
c=Curve[t, f(t), t, -20, 20]
Varje punkt på kurvan har koordinaterna \((t,f(t))\). Genom att avbilda motsvarande vektor med hjälp av en linjär avbildningsmatris, får man
en transformerad kurva. För att göra detta i GeoGebra: skapa punkter och vektorer enligt beskrivningen i avsnittet ovan.
Använd sedan kommandot ApplyMatrix på kurvan.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License