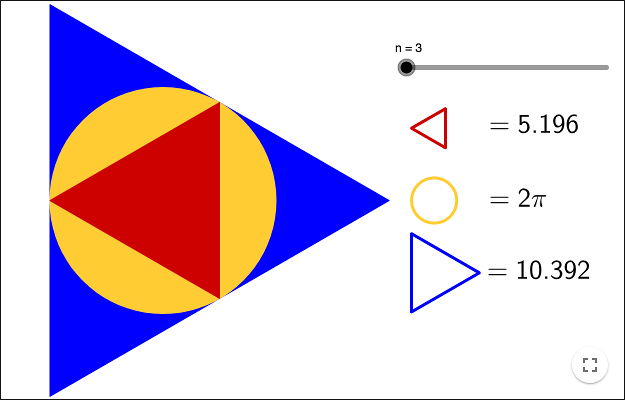
Approximera π

Matematisk analys bygger på gränsvärden. Några av de mest kända exemplen på gränsvärdesberäkningar är olika försök att bestämma närmevärden till \(\pi \). Genom att bestämma gränsvärdet av en polygons area/omkrets då antalet hörn går mot oändligheten, får man en approximation av en cirkels area/omkrets. Cirkelns area/omkrets kan sedan användas för att bestämma ett närmevärde till \(\pi \).

Ladda GeoGebra-arbetsblad

Talet \(\pi \) definieras som förhållandet mellan en cirkels omkrets och dess diameter.

\[\pi=\frac{O}{d}=\frac{O}{2r} \]

Man kan antingen använda denna definition (omkretsen), eller förhållandet mellan en cirkels area och kvadraten av dess radie,

för att bestämma ett närmevärde till \(\pi \).

Genom historiens gång har bägge dessa metoder använts.

Arkimedes pi (≈250 BC)

Arkimedes använde detta faktum

för att bestämma ett närmevärde till \(\pi \).

Han använde en 96-sidig polygon och fick fram följande uppskattning:

\[\frac{223}{71} \lt \pi \lt \frac{22}{7}\]

Denna metod är lätt att använda om man kan använda trigonometri. Arkimedes använde emellertid endast geometri och grekiska siffror!

Liu Huis pi (≈250 AD)

Liu Hui använde areor och insåg att:

Han använde det faktum att om du känner till sidan i en regelbunden \(n\)-hörning, så kan du bestämma sidan i en regelbunden 2\(n\)-hörning.

Precis som Arkimedes använde han inte trigonometri och inte decimala tal.

Liu Huis metod

Det här är inte hela metoden, bara några detaljer. (Googla för mer information)

Börja med en cirkel med radie \(r\) och en regelbunden \(n\)-hörning med en känd sida \(s_0\).

Bestäm sidan av polygonen med \(2n\) sidor, \(s_1\), uttryckt i \(r\) och \(s_0\). Använd inte trigonometri.

Övning

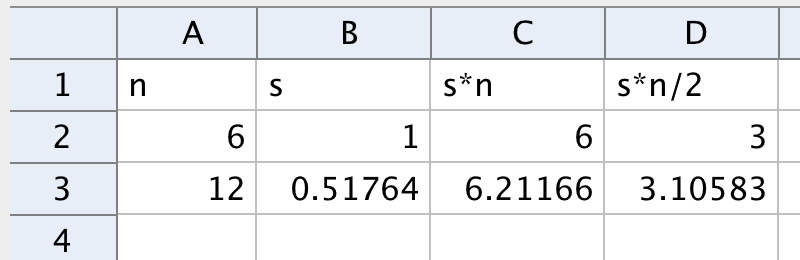
Liu Huis metod med hjälp av kalkylblad

1. Bestäm sidan i en hexagon uttryckt i radien \(r\). Varför är det så enkelt att börja med just en hexagon?
2. Hitta på en radie med valfri längd. Låt \(s_0\) vara sidlängden i den regelbundna hexagonen, \(s_1\) sidlängden i en regelbunden dodekahedron, \(s_2\) längden i en regelbunden 24-hörning, och så vidare. Bestäm en rekursionsformel för \(s_n\).
3. Använd rekursionsformeln du fått fram och ett kalkylblad för att approximera \(π\). Det är enklare att använda omkrets än att använda area (eftersom du, till skillnad från Liu Hui, kan använda ett behändigt talsystem och en dator).

Och sedan?

Anledningen till att Liu Hui använde areor istället för omkrets var att han kom på ett smart sätt att approximera en polygons area med ett rationellt tal, på så vis behövde han inte ta kvadratroten ur upprepade gånger.

Det finns inga kända noteringar om att \(\pi\) approximerades innan Arkimedes gjorde det. De som talar om tidigare approximationer hänvisar inte till några källor där någon av konstanten \(\pi\) s egenskaper faktiskt framgår.

Arkimedes använde rationella tal som approximationer till kvadratrötter. Han approximerade \(\sqrt{3}\) till 5 korrekta gällande siffror. Det är inte känt hur han gjorde det.

Arkimedes (≈250 BC) använde en 96-hörning.

Liu Hui (≈250 AD) använde en 3072-hörning.

Zu Chongzhi (≈500 AD) använde en 12 288-hörning och kom fram till att \(\pi \approx 3.1415962\), vilket var korrekt med 8 gällande siffror.

↓ 900 år senare

Madhava av Sanganagrama (≈1400 AD) kom fram till 10 korrekta gällande siffror genom att använda en serie som sedan kom att kallas Leibniz serie.

Leibniz upptäckte denna serie ≈1700 AD och bevisade att den stämde.

↑ 300 år senare

Formeln, lösning

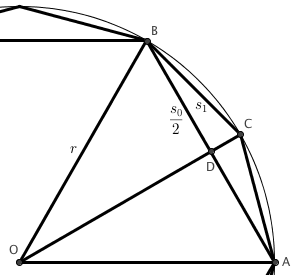
Börja med en cirkel med radie r och en n-gon med en känd sida \(s_0\).

I bilden till höger är \(OB=OC=r\).

Använd Pythagoras sats på triangeln \(\Delta OBD\):

\[OD=\sqrt{r^2-\frac{s_0^2}{4}}\]

Längden blir

\[CD=r-OD=r-\sqrt{r^2-\frac{s_0^2}{4}}\]

Använd Pythagoras sats på triangeln \(\Delta BCD\):

\[BC=\sqrt{BD^2+CD^2}=\sqrt{\frac{s_0^2}{4}+\left(r-\sqrt{r^2-\frac{s_0^2}{4}}\right)^2} \]

Detta kan förenklas som nedan.

\[BC=\sqrt{\frac{s_0^2}{4}+r^2-2r\sqrt{r^2-\frac{s_0^2}{4}}+\left(r^2-\frac{s_0^2}{4} \right)} = \sqrt{2r^2-2r\sqrt{r^2-\frac{s_0^2}{4}}}\]

Den sista förenklingen behövs inte för att skriva in formeln i kalkylbladet.

En hexagon

En regelbunden hexagon kan delas upp i sex liksidiga trianglar med de inre vinklarna 60°. Om hexagonen läggs in i en cirkel med radien 1, kommer hexagonens sidlängd att vara 1. Vi får följande rekursionsformel för polygonernas sidlängder:

\[ \left\{ \begin{eqnarray} s_0 &=& 1 \\ s_{n+1} &=& \sqrt{2-2\sqrt{1-\frac{s_n^2}{4}}} \end{eqnarray} \right. \]

där \(s_0\) är hexagonens sidlängd och \(s_n\) sidlängden till en \(6\cdot 2^n\)-hörning då \(n > 1\).