Komplexa tal

I GeoGebra kan du skriva in ett komplext tal i inmatningsraden genom att använda \(i\) som den imaginära enheten; exempelvis w=2+3i. Talet dyker upp i ritytan som en punkt vilken du kan flytta. Du kan också använda verktyget Komplext tal.

Det finns GeoGebra-funktioner som verkar på både komplexa tal och punkter. Funktionerna abs(w), arg(w) och conjugate(w) behöver ingen förklaring. För att få realdelen respektive imaginärdelen använder du x(w) respektive y(w).

Du kan använda aritmetiska operationer på komplexa tal och vissa komplexvärda funktioner fungerar.

Komplexvärda funktioner av en komplex variabel

För en funktion som avbildar ett komplext tal på ett komplext tal går det inte att använda en graf i ett koordinatsystem. Man kan däremot i vissa fall visualisera en avbildning genom att beskriva hur en mängd i det komplexa talplanet avbildas på en annan mängd.

Vi ska använda följande metoder i GeoGebra för att visualisera en komplexvärd funktion av en komplex variabel.

Metod 1 kan användas för att studera hur en mängd punkter avbildas på en annan mängd punkter.

Om du vill studera hur en mängd punkter som utgör någon kurva avbildas, kan du använda verktyget Geometrisk ort.

Om du vill avbilda en polygon kan du placera en komplex punkt på varje sida i polygonen och sedan använda Metod 2 på varje punkt. Detta förfarande blir tidsödande om du vill avbilda flera polygoner och går att effektivisera med hjälp av GeoGebras kalkylblad.

Notera att dessa metoder inte fungerar på funktioner som explicit beror på \(\text{Re } z \), \(\text{Im } z\), \(\text{arg } z\) eller \(\bar{z}\). Metoderna fungerar inte heller med polynomfunktioner med komplexa koefficienter. En förutsättning för att metoderna fungerar är att funktionen också kan skrivas som en reellvärd funktion av ett reellt tal.

Om du vill använda en enkel funktion \(f(z) = az + b\) där \(a\) och \(b\) är komplexa koefficienter, kan du skriva in uttrycket a*z_1+b för att skapa den avbildade punkten.

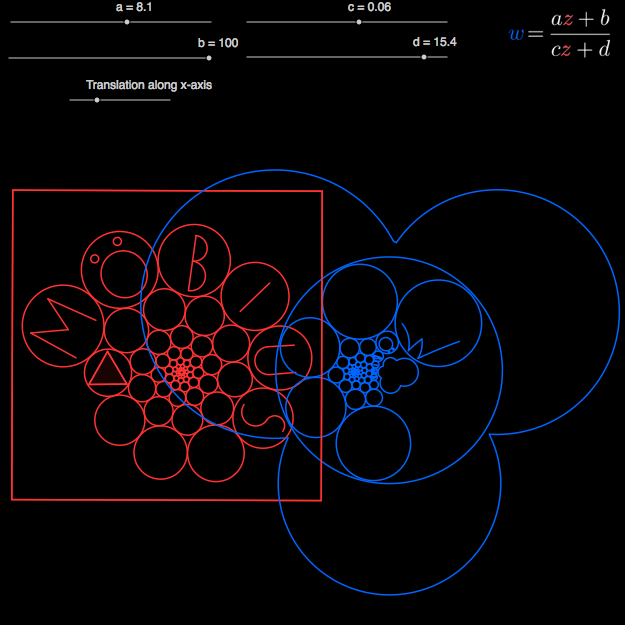
Möbiusavbildningar

Ladda GeoGebra-arbetsblad

En Möbiusavbildning är en funktion \(\mathbb{C} \rightarrow \mathbb{C}\) som ges av

där \(a, b, c\) och \(d\) är komplexa tal sådana att \(ad-bc\ne 0\).

En Möbiusavbildning är inte definierad då \(z = -d/c\) eftersom detta innebär division med noll. Om vi istället använder det så kallade utvidgade komplexa talplanet innefattar detta även en punkt i oändligheten. Det utvidgade komplexa talplanet representeras av punkter på den så kallade Riemannsfären där punkten i oändligheten är den punkt som ligger överst på sfären.

Genom att använda Riemannsfären, vilken vi kan skriva som \(\mathbb{C} \cup \{\infty \} \), kan vi definiera en Möbiusavbildning \(\mathbb{C} \cup \{\infty \} \rightarrow \mathbb{C} \cup \{\infty \} \) på följande sätt:

Vi förutsätter att \(ad-bc\ne 0\).

Om \(c \ne 0 \) definierar vi funktionen som

Om \(c = 0\) definierar vi funktionen som

Notera att om \(c \ne 0\) kan inte \(d = 0\) eftersom \(ad-bc\ne 0\).

Följande två egenskaper för Möbiusavbildningar visas lätt:

1. Om \(f\) och \(g\) är Möbiusavbildningar så är även \(f \circ g\) en Möbiusavbildning. Med andra ord är även \(f(g(z)\) en Möbiusavbildning.
2. En Möbiusavbildning \(f\) har alltid en invers \(f^{-1}\). Med andra ord finns det en funktion \(f^{-1}\) sådan att \(f(f^{-1}(z)) = f^{-1}(f(z)) = z\).

Att sammansättningen av Möbiusavbildningar är en Möbiusavbildning innebär att upprepade transformationer kan beskrivas som sammansättning av funktioner.

Övningar

Många övningar förutsätter att du känner till spegling i cirkel: Non-Euclidean Geometry ‐ Inversion in Circle.

Övning 1

Mängder i det komplexa talplanet

Beskriv följande mängder genom att rita på papper med en penna.

• \(1 < \text{Re } z < 5\)
• \(0 < \arg z < \pi/4\)
• \(|z-(2+i)| < 3\)

Övning 2

Bestäm mängden

Låt \(z\) och \(w\) vara komplexa tal sådana att

• Använd Metod 1 för att göra en GeoGebra-konstruktion av avbildningen.

• Mängden \(\text{Re } z > 0\) avbildas på en mängd som kan skrivas som någon ekvation i \(w\). Använd din GeoGebra-konstruktion för att ta reda på hur denna mängd ser ut och formulera ett påstående. Tips: lägg spår på punkterna!

• Bevisa ditt påstående.

• Bestäm den inversa funktionen \(f^{-1}\) till \(f(z)= (z-1)/(z+1)\).

Övning 3

Jämför med spegling i cirkel

• Lägg in en komplex punkt \(z_1\) i GeoGebra. Skapa punkten \(1/z_1\).

  Gör en enhetscirkel och spegla \(z_1\) i enhetscirkeln med hjälp av verktyget Speglingspunkt till cirkel.

  Jämför de två operationerna \(1/z\) och spegling av \(z\) i enhetscirkel och beskriv vilket samband det finns mellan dessa operationer.

• Bestäm den komplexvärda funktion som motsvarar spegling i enhetscirkeln. Hur skiljer sig denna från funktionen \(f\)?

• Rotationer, speglingar och translationer är vinkelbevarande transformationer. Vi har också tidigare visat att vinklar bevaras vid spegling i cirkel. Är funktionen \(f(z) = 1/z\) vinkelbevarande eller inte? Motivera ditt svar.

Övning 4

Komplex aritmetik och transformationer

En Möbiusavbildning kan delas upp i fyra funktioner

• \( f_1(z) = z + d/c \)
• \( f_2(z) = 1/z \)
• \( f_3(z) = \frac{bc-ad}{c^2} z \)
• \( f_4(z) = z + a/c \)

sådana att

• Lägg in två komplexa punkter \(z_1\) och \(a\). Skapa två punkter \(z_1+a\) och \(z_1\cdot a\). Dra i punkten \(a\), exempelvis längs \(x\)- och \(y\)-axeln.

  Beskriv addition och multiplikation av komplexa tal som transformationer. Förklara varför dina beskrivningar stämmer. I din förklaring bör du använda att ett komplext tal både kan skrivas på formen \(a+bi\) och på polär form som \(re^{i\theta}\).

• Du kan förutsätta att spegling i cirkel är en vinkelbevarande operation. Använd uppdelning i enkla transformationer till att argumentera för att Möbiusavbildningar bevarar vinklar.

Övning 5

Avbildning av cirkel

Använd Metod 2 för att visualisera hur en cirkel avbildas av funktionen

samt hur en cirkel avbildas av funktionen

När du gjort din konstruktion ska du kunna förändra cirkeln genom att dra i de punkter som definierar cirkeln. Färglägg kurvorna så att du kan se vilken kurva som hör till vilken funktion.

• För funktionen \(f\) bör du kunna gissa vilken sorts kurva cirkeln avbildas på. Hur kan du resonera kring denna kurva?

• Finns det några enkla fall av cirklar där du lätt kan förstå vilken sorts kurva som avbildas av funktionen \(g\)?

Övning 6

Avbildning av linje

Använd Metod 2 för att visualisera hur en linje avbildas av funktionen

samt hur en linje avbildas av funktionen

• För funktionen \(f\) bör du kunna gissa vilken sorts kurva linjen avbildas på. Hur kan du resonera kring denna kurva?

• Finns det några enkla fall av linjer där du lätt kan förstå vilken sorts kurva som avbildas av funktionen \(g\)?

Övning 7

Avbildning av kvadrat och triangel

• Använd Metod 3 för att visa hur en kvadrat och en regelbunden triangel avbildas av funktionen

  \[f(z) = \frac{1}{z}.\]

• Du ska nu också visa hur polygonerna avbildas av funktionerna

  \[g(z) = az\]

  och

  \[h(z) = z + a\]

  där \(a\) är en komplex koefficient. Lägg in en komplex punkt som representerar koefficienten \(a\).

  Använd kolumn D och E för att visa hur polygonerna avbildas av \(g\). Använd kolumn F och G för att visa hur polygonerna avbildas av \(h\). Det går inte att använda GeoGebra-funktioner för detta men det går att skriva in uttrycken direkt.

• Beskriv och förklara de transformationer som åstadkoms av \(f, g\) och \(h\).

Övning 8

Möbiusavbildning av polygon

För enkelhetens skull ska vi här bara använda reella koefficienter \(a, b, c, d\). Gör en glidare för varje koefficient och skriv en funktion \(f(x)\) för en Möbiusavbildning som definieras med hjälp av glidarna.

Gör en GeoGebra-konstruktion som visualiserar hur en valfri regelbunden polygon transformeras av funktionen.

• Vilka sorts transformationer kan du åstadkomma om du utgår ifrån att \(c = 0\)?

• Vilken sorts transformation kan du inte åstadkomma eftersom koefficienterna är reella?