Funktioner

Det finns ett antal fördefinierade funktioner och operatorer i GeoGebra som visas på sidan GeoGebra - Predefined Functions and Operators. I normalfallet kan man gissa sig till hur en funktion ska skrivas.

Om du skriver ett uttryck av \(x\) i inmatningsfältet, skapas en funktion som GeoGebra namnger. Du kan också namnge en funktion själv genom att exempelvis skriva:

minFunktion(x) = sin(x)

Det är enkelt att hantera funktioner med koefficienter i GeoGebra. Koefficienterna kan representeras av glidare. Om du exempelvis vill visa en polynomfunktion av grad tre, lägger du in fyra glidare \(a, b, c, d\), och skriver sedan in funktionen:

f(x)=ax^3+bx^2+cx+d

i inmatningsfältet.

Du kan visa ett dynamiskt funktionsuttryck i ritområdet genom att lägga in text. Skriv in f(x)= i textediteringsfönstret och välj sedan \(f\) ur Objekt-menyn. Markera LaTeX-formel.

\(f(x)\)-notation och ekvationer i \(y\) och \(x\)

Om du skriver in följande funktioner i inmatningsfältet (en i taget):

y = 2x-1
y = x^2+1
y = x^3-x^2+x-1

och sedan betraktar algebrafönstret, ser du att GeoGebra skapet tre olika sorters objekt: en linje, ett kägelsnitt och en funktion. Alla tre objekt har fått namn av GeoGebra.

En kurva definierad av en ekvation i \(y\) och \(x\) är ett mer generellt begrepp än grafen till en funktion. Alla sådana kurvor kan inte vara grafen till en funktion.

När det gäller linjer, kan du skriva in x = 5 och få en vertikal linje, vilket inte kan vara grafen till en funktion.

När det gäller kägelsnitt, kan du skriva in ekvationen för vilket kägelsnitt som helst. I det allmänna fallet en ekvation på formen

\[ax^2+bxy+cy^2+dx+ey +f=0\]

där koefficienterna antingen representeras av glidare eller skrivs som tal.

Den skillnad som görs av GeoGebra (mellan linjer, kägelsnitt och funktioner) spelar ingen roll så länge du inte vill ägna dig åt matematisk analys. Om du däremot vill ägna dig åt matematisk analys, så fungerar bara kommandona på objekt som är funktioner. I sådant fall bör du använda \(f(x)\)-notation, dvs skriva in funktionerna som:

f(x) = 2x-1
g(x) = x^2+1
h(x) = x^3-x^2+x-1

Koefficienter representerade av glidare

För elever som just börjat studera matematiska funktioner, kan det vara en svårbegriplig abstraktion att använda bokstäver som beteckningar för koefficienter. I uttrycket

\[y = kx + m,\]

står bokstäverna \(y\) och \(x\) för variabler, medan bokstäverna \(k\) och \(m\) betecknar konstanta tal. För nybörjare kan det vara en god idé att inledningsvis undvika glidare och istället börja med exempelfunktioner där koefficienterna skrivs som tal.

\[ \begin{align*} y &= x \\ y &= -x \\ y &= 2x \\ y &= 2x +2 \\ y &= 2x -3 \end{align*} \]

När eleverna väl förstått begreppen lutning och skärning med \(y\)-axeln, kan du introducera glidare \(k\) och \(m\) för att studera en allmän linjär funktion. När eleverna väl förstått begreppet koefficient, kan glidare användas för alla funktioner.

Skala om axlarna

Det enklaste sättet att skala om axlarna är att trycka på Shift och dra musen över en av axlarna. Då musmarkören ändrar utseende, kan du dra i axeln genom att trycka ner vänster musknapp och dra.

Det går också att skala om genom att markera verktyget Flytta ritområde och sedan dra i axlarna.

Vill du ändra tillbaka skalan till förhållandet 1:1, klickar Alt+M eller Cmd+M. Vill du ha ett annat förhållande, högerklickar du någonstans i ritområdet där det inte finns ett objekt, och väljer xAxeln:yAxeln.

Funktionsinspektören

Med verktyget Funktionsinspektör kan du inspektera en funktion.

Du kan använda detta verktyget till att inspektera en funktion i ett intervall

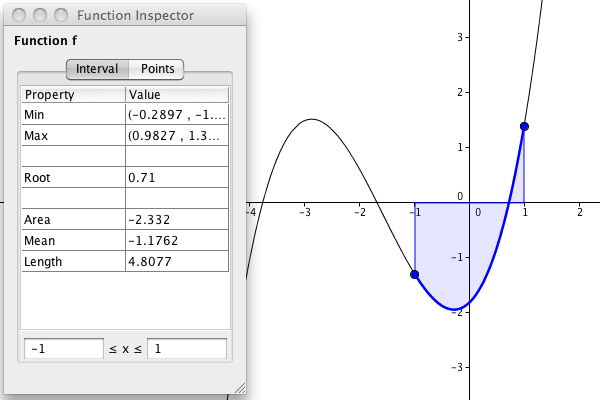
eller kring en punkt.

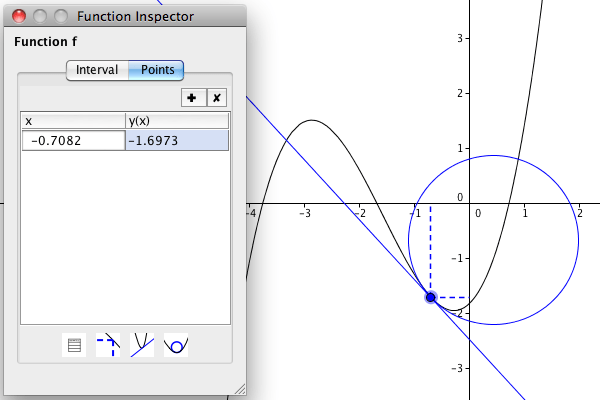
Grader och radianer

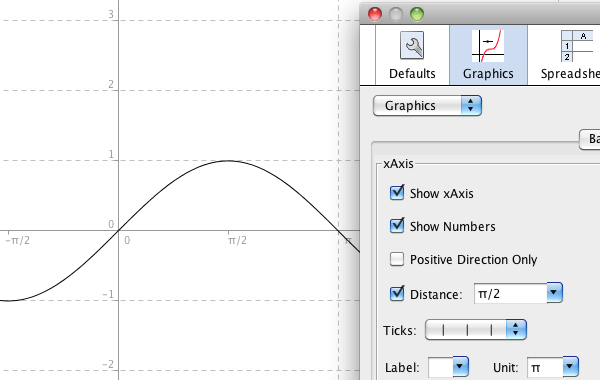
När du skriver in en trigonometrisk funktion så är den förvalda enheten radianer. Om du använder radianer, kan du ställa in enheten för \(x\)-axeln till att vara \(\pi\). Högerklicka på ritområdet och välj Ritområde.

Vill du använda grader som enhet, så lägger du till ett grad-tecken efter \(x\). Skriv in funktionen: f(x)=sin(x°). Kort-kommandot för att skriva ett grad-tecken är Ctrl+O. Du kan ställa in grader som enhet för \(x\)-axeln.

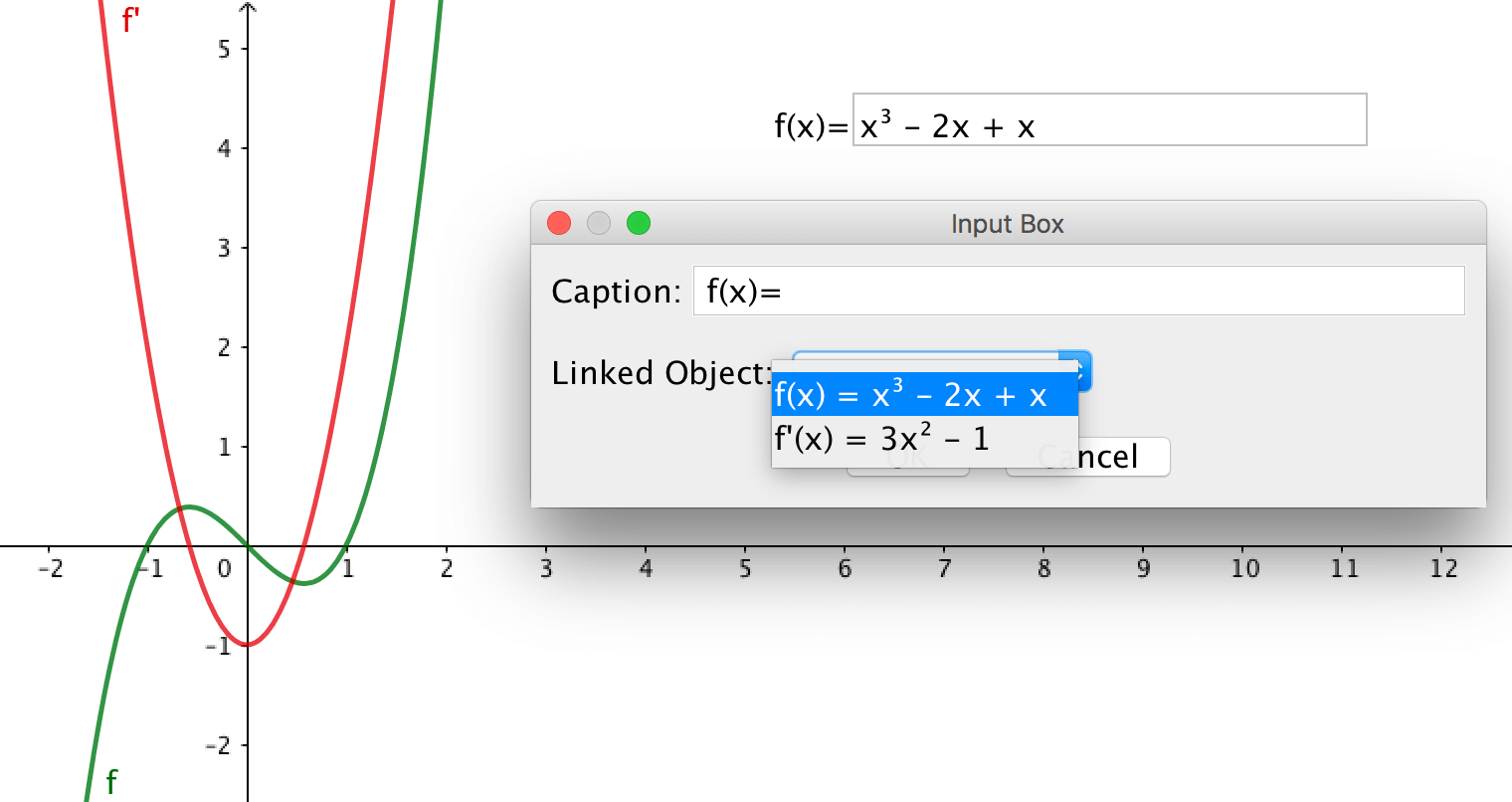
Interaktiva inmatningsrutor

Du kan länka ett inmatningsfält i ritområdet till ett GeoGebra objekt. Använd verktyget Inmatningsfält och klicka i ritområdet. Om du kopplar ett inmatningsfält till en funktion, bör funktionsuttrycket skrivas in med samma syntax som används i det vanliga inmatningsfältet, med exempelvis ^ för upphöjt till.

Sammansatta funktioner

Om \(f\) och \(g\) är två funktioner som du definierat i GeoGebra, kan du skapa en sammansatt funktion genom att skriva

f(g(x))

i inmatningsfältet.

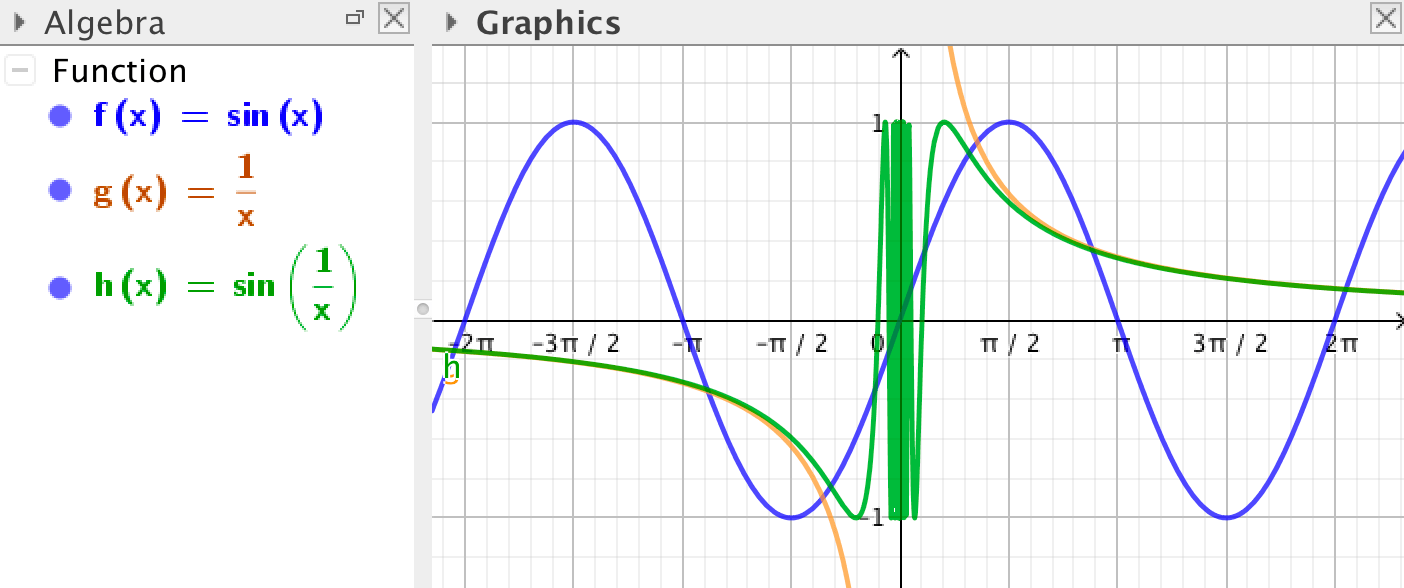
Om \(g(x) = \dfrac{1}{x}\) kan du också skriva

f(1/x)

eller något annat uttryck i \(x\) innanför parenteserna.

Olikheter

Om du har två uttryck i \(x\), kan du visa för vilka intervall en olikhet gäller. Du kan exempelvis skriva in följande kod i inmatningsraden:

x^2<=x+1

Så här skriver man olikheter i GeoGebra: <, >, <=, >= betyder <, >, ≤ respektive ≥

Styckvis definierade funktioner

En styckvis definierad funktion är definierad på olika vis i olika intervall. I GeoGebra kan du definiera en funktion på ett intervall med kommandot Funktion( <Funktion>, <Från x-Värde>, <Till x-Värde> ).

Funktionerna ovan skrivs:

f(x)=Function(1,-10,-1)
g(x)=Function(x^2,-1,1)
h(x)=Function(2x-1,1,10)
f_der(x)=Function(f'(x),-10,-1)
g_der(x)=Function(g'(x),-1,1)
h_der(x)=Function(h'(x),1,10)

Kommandon för funktioner

Om funktionen heter \(f\) kan du använda kommandot f'(x) för att skapa derivatans funktion.

Med kommandot Integral[f, <Från>, <Till>] beräknas integralen och arean visas i ritområdet.

Om du placerar en punkt på grafen, kan du använda kommandona Krökning[<Punkt>,<Funktion>] och Krökningsvektor[<Punkt>,<Funktion>] för att visa den oskulerande cirkeln.

Om funktionen är en polynomfunktion finns dessutom kommandona Extrempunkt[<Funktion>] och Inflexionspunkt[<Funktion>].

Du kan använda kommandot Taylorutveckling(f, <x-värde>, <Ordningsnummer> ) till att Taylorutveckla en funktion.

Trappstegsfunktioner

Det finns kommandon i GeoGebra för att göra trappstegsfunktioner. Givet en funktion \(f\), kan du göra tre olika sorters trappstegsfunktioner:

Undersumma(f, <Från x>, <Till x>, <Antal rektanglar>)

Översumma(f, <Från x>, <Till x>, <Antal rektanglar>)

TrapetsSumma(f, <Från x>, <Till x>, <Antal trapetser>)

Övningar

Övning 1

Transformationer av grafer

Del 1

Lägg in en glidare \(a\). Gör en funktion \(f(x) = x^2\).

Gör fyra funktioner \(g(x) = f(x+a)\), \(h(x) = f(x)+a\), \(p(x) = f(a\cdot x)\) och \(q(x) = a\cdot f(x)\).

Del 2

Ett arbetsblad som innehåller fem funktioner kan vara svåranvänd eftersom det innehåller för mycket information. Du kan använda verktyget Checkbox för att dölja/visa objekt.

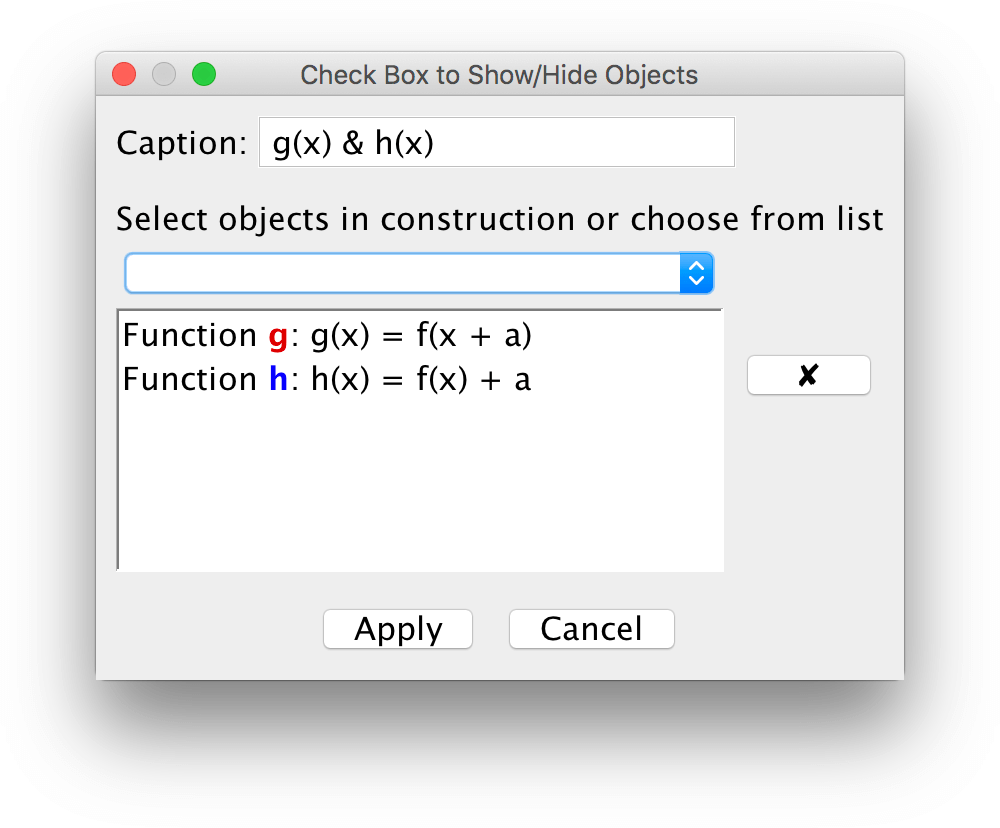
Se till att funktionerna \(g, h, p, q\) kan visas/döljas parvis.

Eftersom de slutsatser man kan dra om transformationer av grafer gäller generellt, är det bra om man kan byta funktion. Använd verktyget Inmatningsfält och se till att användaren lätt kan definiera om funktionen \(f\).

Välj själv om du vill ha med förklarande texter.

Studera hur grafen till de fyra funktionerna ändrar sig när du drar i glidaren \(a\). Varje transformation kan beskrivas som en förflyttning ett antal enheter i någon riktning, eller som en utdragning längs någon koordinataxel med någon faktor.

Beskriv varje transformation med ord. Beskriv speciellt vad som händer då \(a = -1\). Vissa transformationer är lättare att se om \(f(x) = e^x\) eller \(f(x) = \sin(x)\). Definiera om \(f(x)\) med hjälp av inmatningsfältet.

Övning 2

Från enhetscirkel till sinusfunktion

Börja med att se till att alla vinklar använder enheten radianer. Välj menyn Inställningar -> Avancerat och gör inställningen under Vinkelmått.

Se till att \(x\)-axeln är indelad med avståndet \(\pi/2\).

Gör en enhetscirkel, tre punkter och en vinkel \(\alpha\) som i bilden nedan.

Skapa en punkt P = (α, y(A)) och dra punkten \(A\) runt enhetscirkeln.

För att markera att det handlar om en \(y\)-koordinat, kan du lägga in två sträckor: Sträcka((x(A), 0), A) och Sträcka((x(P), 0), P).

Det finns nu olika sätt att rita upp sinusfunktionens graf. Testa alla tre!

Lägg ett spår på punkten \(P\) och dra i punkten \(A\).
Använd verktyget Geometrisk ort. Klicka först på \(P\) och sedan på \(A\).
Skapa en funktion med en begränsad definitionsmängd med kommandot Funktion( sin(x), 0, α ).

Övning 3

Från enhetscirkel till tangensfunktionen

Gör en enhetscirkel, tre punkter och en vinkel \(\alpha\). Skapa också linjen \(x=1\).

Placera en punkt \(B\) på linjen \(x=1\) som också ligger på linjen mellan \(O\) och \(A\), med beteckningar som i bilden nedan.

Skapa en punkt \(P\) som har vinkeln \(\alpha\) som \(x\)-koordinat och samma \(y\)-koordinat som punkten \(B\).

Rita upp grafen genom att: lägga ett spår på \(P\), använda verktyget Geometrisk ort, eller genom att skapa en funktion med begränsad definitionsmängd. Som i Övning 2.

Övning 4

Från lutning till derivata

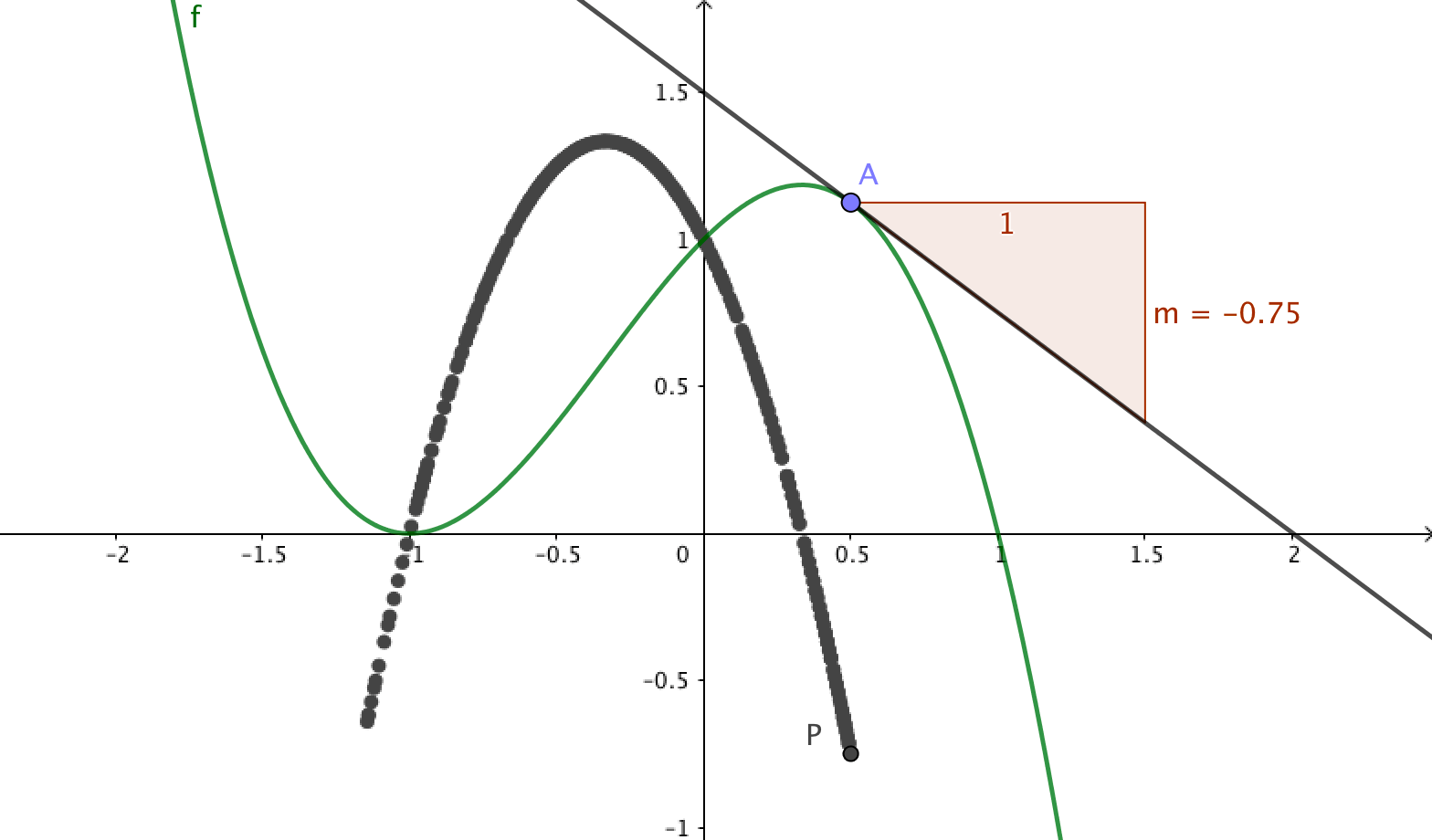
Definiera en valfri funktion \(f(x) \). Lägg en punkt \(A\) på grafen. Använd verktyget Tangent och lägg in en tangent till \(f\) genom \(A\). Använd verktyget Lutning till att mäta tangentens lutning. Lutningen sparas i en variabel \(k\) (på engelska används bokstaven \(m\)).

Gör en punkt \(P\) som har samma \(x\)-koordinat som \(A\) och lutningen \(k\) som \(y\)-koordinat.

Nu kan du visa derivatans graf på tre sätt.

Lägg ett spår på punkten \(P\) och dra i punkten \(A\).
Använd verktyget Geometrisk ort. Klicka först på \(P\) och sedan på \(A\).
Visa derivatans graf genom att skriva f' i inmatningsfältet.

Övning 5

Från trappstegsfunktioner till integral

Skriv in en valfri funktion \(f\).
Gör en glidare \(n\) av (positiva) heltal. Glidaren representerar antalet intervall.
Placera två punkter \(A\) och \(B\) på \(x\)-axeln. Punkternas \(x\)-koordinater är intervallets ändpunkter.
Skriv in undersumman: U=Undersumma(f,x(A),x(B),n).
Skriv in översumman: Ö=Översumma(f,x(A),x(B),n).
Skriv in trapetssumman: T=TrapetsSumma(f,x(A),x(B),n).
Skriv in integralen: I=Integral(f,x(A),x(B)).