Triangeldefinition
Genom historien har likformiga trianglar använts för att uppskatta avstånd som inte kan mätas direkt. Innan man hade miniräknare eller datorer, användes olika sorters trigonometriska tabeller som visade sidlängder av trianglar för olika vinklar.
Triangeldefinitioner av sinus och cosinus
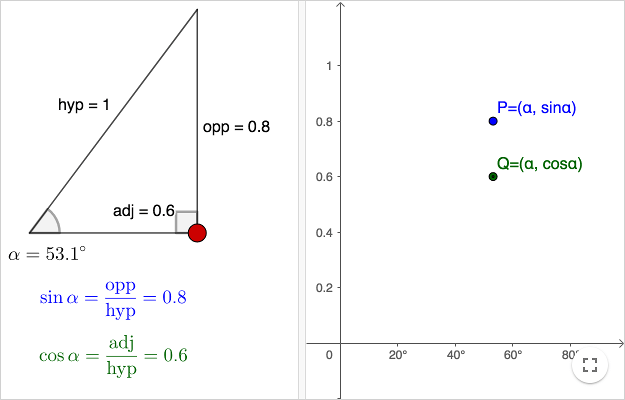
Om man använder beteckningar som i bilden ovan, så definieras de trigonometriska funktionerna så här
\[ \begin{align} \sin \alpha &= \frac {\text{motst}}{\text{hyp}} \\ \cos \alpha &= \frac {\text{närl}}{\text{hyp}} \\ \tan \alpha &= \frac {\text{motst}}{\text{närl}} = \frac{\sin \alpha}{\cos \alpha} \end{align} \]Förkortningarna står för hypotenusa, motstående och närliggande (relativt vinkeln \(\alpha\)).
Eftersom förhållandet mellan två sidor i en triangel inte beror på triangelns storlek, kan vi använda den enkla storleken att hypotenusan är ett. Om hypotenusan är konstant, kan vi skapa två funktioner sinus och cosinus som båda är funktioner av vinkeln \(\alpha\). För att \(\alpha\) ska kunna vara en av de icke-rätvinkliga vinklarna i en rätvinklig triangel, måste det gälla att \(0 \lt \alpha \lt 90^\circ\).
Inverterade trigonometriska funktioner
Om man skall bilda förhållandet mellan två sidor i en triangel, så kan detta göras på sex olika sätt. De tre förhållanden som oftast används är sinus, cosinus och tangens. Alla sex förhållanden har dock namn. De tre mindre vanliga förhållanden är cosecant (\(\csc \)), secant (\(\sec \)) och cotangens (\(\cot \)). Dessa definieras så här:
\[\csc \alpha = \frac {\text{hyp}}{\text{mots}} = \frac{1}{\sin \alpha}\]
\[\sec \alpha = \frac {\text{hyp}}{\text{närl}} = \frac{1}{\cos \alpha} \]
\[\cot \alpha = \frac {\text{närl}}{\text{mots}} = \frac{1}{\tan \alpha}\]
Några historiska tabeller
Nuförtiden kan man använda en miniräknare eller dator till att ta reda på värden till trigonometriska funktioner. Om man inte är ovanligt vetgirig, behöver man inte ens veta hur en dator gör för att ta fram värdet av sinus för en vinkel. Förr i tiden använde de däremot trigonometriska tabeller.
Tabeller av kordor i det antika Grekland
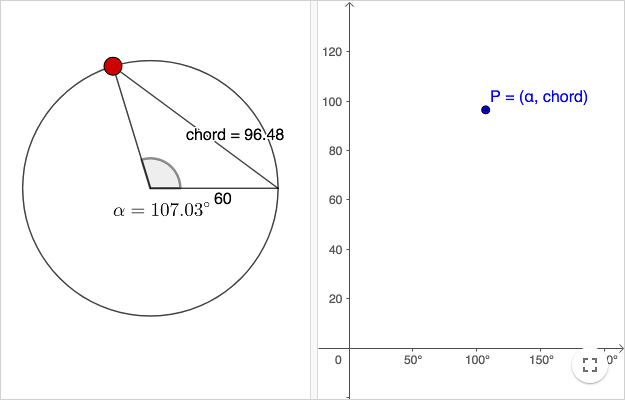
Den första trigonometriska tabellen gjordes av Hipparchus ( ≈ 150 f.Kr ) som också anses vara trigonometrins fader. Hipparchus originalarbete finns inte bevarat men Ptolemaeus ( ≈ 150 e.Kr ) refererar till honom i sin berömda bok Almagest. I Almagest finns det trigonometriska tabeller av kordor. En korda är en sträcka vars ändpunkter ligger på en cirkel. Ptolemaeus använde basen 60 då han räknade och han använde grader för att mäta vinklar.
Kordan som funktion av vinkeln, vilken visas i arbetsbladet ovan, är en anakronism (liksom arbetsbladet). Att plotta grafer av funktioner gjordes först många århundraden efter Ptolemaeus.
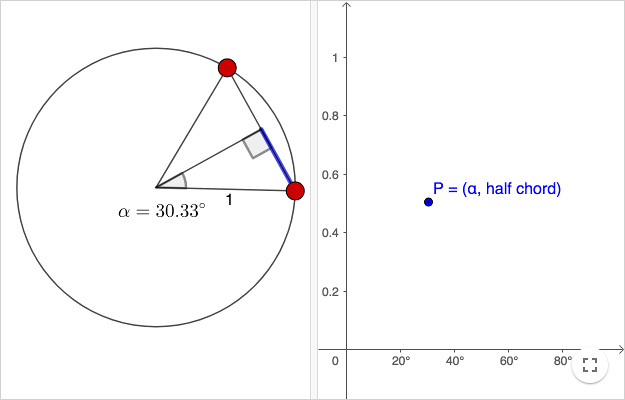
Tabeller av halva kordor i Indien
Den indiske matematikern Aryabhata ( ≈ 500 e.Kr ) var den förste som gjorde en tabell av halva kordor istället för av kordor. Då man använder kordor är trianglarna likbenta. Då man använder halva kordor är trianglarna rätvinkliga.
Ordet sinus etymologi
Aryabhata kallade sina halva kordor för ardha-jya (på sanskrit), vilket förkortades till jya. Från detta ord myntade araberna ordet jiba som betyder halv korda. Eftersom vokaler inte skrevs ut, skrev man ordet jiba som jb. Då mathematiken/vetenskapen återvände till Europa (≈ 1 K år efter Ptolemaeus), trodde europeiska vetenskapsmän att jb stod för jaib, vilket betydde "grotta" eller "bukt". De översatte därför fel ord till det latinska ordet sinus.
Exakta vinklar
De exakta värdena av sinus och cosinus för vinklarna \(30^\circ, 45^\circ\) och \(60^\circ \); kan bestämmas med hjälp av trianglarna i bilden nedan.
Utöver dessa välkända vinklar finns det även andra vinklar som ger upphov till exakta värden av sinus och cosinus. I boken Almagest av Ptolemaeus, beräknas kordorna för vinklarna \(36^\circ \) och \(72^\circ \).
Den gyllene triangeln
Talen \(36, 72\) and \(108\), har egenskaperna att \(2\cdot 36 = 72\) och \(3\cdot 36 = 108\). Dessutom gäller det att: \[72+108=72+72+36=108+36+36=180\]
Om man startar med den likbenta triangeln till vänster i bilden nedan, kan man konstruera två likbenta trianglar genom att dra bisektrisen till en av \(72^\circ \)-vinklarna.
Om man betraktar de inre vinklarna i en regelbunden femhörning
finner man att man kan konstruera ett antal olika självupprepande mönster av pentagoner och pentagram som innehåller vinklarna \(36^\circ, 72^\circ, 108^\circ\) - och inga andra vinklar.
Triangeln kallas den gyllene triangeln eftersom förhållandet mellan sidorna i triangeln är det gyllene snittet.
Övningar
Övning 1
Använd likformighet för att ställa upp en andragradsekvation för \(x\) (med beteckningar från bilden till höger). Visa att förhållandet mellan sidorna i den gyllene triangeln är det gyllene snittet genom att lösa andragradsekvationen.
Övning 2
Bestäm de exakta värdena av \(\cos 36^\circ \) och \(\cos 72^\circ \).
Utvidgning av definitionerna
De trigonometriska förhållandena kan ses som funktioner av en vinkel. Det är grafen av dessa funktioner som ritas i de tre interaktiva exemplen ovan. Om vinkeln kallas \(x\), så är funktionerna bara definierade för \(0\lt x \lt 90^\circ\), annars kan \(x\) inte vara en icke-rät vinkel i en rätvinklig triangel. Man kan utvidga definitionerna av de trigonometriska funktionerna så att de är definierade för alla \(x\). Då man gör sådana definitioner, används en enhetscirkel istället för en rätvinklig triangel.
animerad gif:
Pentagrams på tumblr.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License