Tessellations and Symmetries

A tessellation (or tiling) is a pattern of geometrical objects that covers the plane. The geometrical objects must leave no holes in the pattern and they must not overlap. You should be able to extend the pattern to infinity (in theory). You make a tessellation by starting with one or several figures and then you rotate, translate or reflect them; or do a combination of transformations, in order to get a repeating pattern.

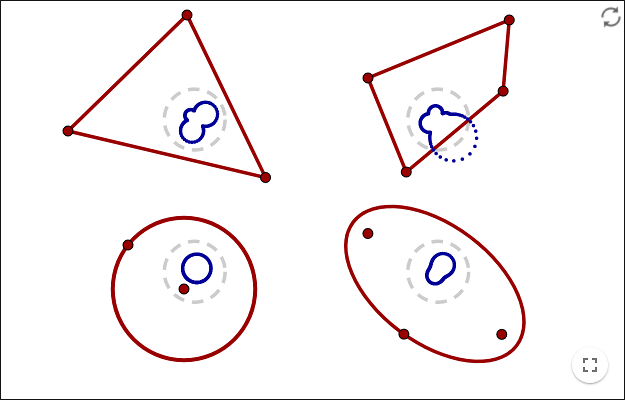
If you only want to use one regular polygon to make a tessellation, there are only three possible polygons to use: triangle, square and hexagon. Click on the triangle and square in the example above to see the other two possible tilings of regular polygons.

Starting with a tiling of regular polygons, you can distort it (as shown above). It is possible to distort it in many different ways. In the example above:

• The triangle tiling is distorted to a tiling of two different tiles.
• The square tiling is distorted to a tiling of one tile. All tiles are translations of the tile in the centre.
• The hexagon tiling is also distorted to a tiling of one tile. Every tile is rotated relative to its neighbours.

On the page GeoGebra Tutorial - Symmetries there is a description of how to make a tessellation using GeoGebra.

Symmetries

Translational symmetry is just one type of symmetry. There is also rotational and reflection symmetry.

Load GeoGebra worksheet

Drag the red point to make a painting! Which of the images has a rotational symmetry and which has a reflection symmetry; the blue or the green?

An image has a rotational symmetry if you can rotate the image around some point and get the same image.

An image has a reflection symmetry if you can reflect the image in some line and get the same image.

Reflection in Circle

Load GeoGebra worksheet

Move the red points! De red figures are reflected in the circles onto the blue figures. All angles are preserved when reflected.

Draw a circle mirror image using the red point below!

Load GeoGebra worksheet

For a more advanced painting program, and an explanation of circle-inversion, see Paint Circle-Inverted Mondrian!.

For a hyperbolic tessellation see: Non-Euclidean Geometry - Interactive Hyperbolic Tiling in the Poincaré Disc.