Approximating π

Mathematical calculus is based on the concept of limits. Some of the most famous examples using limits, are the attempts throughout history to find an approximation for \(\pi \). By trying to find the limit of the area/perimeter of a regular polygon as the number of vertices tends to infinity, you get an approximation of the area/circumference of the circle. The area/circumference of a circle can then be used to find an approximation of \(\pi \).

Load GeoGebra worksheet

The number \(\pi \) is defined to be the ratio of the circumference of a circle to its diameter.

\[\pi=\frac{C}{d}=\frac{C}{2r} \]

You can use either the definition (the circumference), or you can use the ratio between the area of a circle and the square of the radius,

\[\pi=\frac{A}{r^2} \],

to approximate \(\pi \).

Throughout history, both these approaches have been used.

Archimedes' pi (≈250 BC)

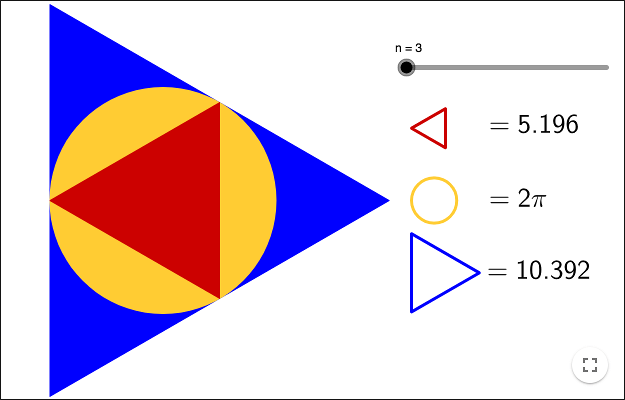
Archimedes used the fact that the circumference of a circle is bounded by the perimeter of an inscribed polygon and the perimeter of a circumscribed polygon. This fact was used to approximate \(\pi \).

Archimedes used a 96-sided polygon to find following approximation:

\[\frac{223}{71} \lt \pi \lt \frac{22}{7}\]

It is easy to use this method by using trigonometry, Archimedes however only used geometry and Greek numerals!

Liu Hui's pi (≈250 AD)

Liu Hui used areas and realized that:

He used the fact that if you know the side in a regular \(n\)-gon, you can find the side in a regular \(2n\)-gon.

Just as Archimedes he didn’t use trigonometry and he didn’t have decimal numbers.

Liu Hui's method

This isn’t the entire method, it is just a few details. (Google on it for more information)

Start with a circle with radius \(r\) and a \(n\)-gon with a known side \(s_0\).

Find the side of the \(2n\)-gon, \(s_1\), in terms of \(r\) and \(s_0\). Do not use trigonometry.

Exercise

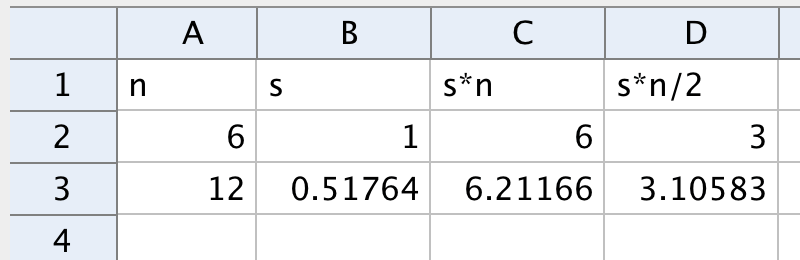
Liu Hui's method using a spreadsheet

1. Find the side of the hexagon in terms of the radius \(r\). Why is a hexagon a good choice for the first polygon?
2. Pick a radius of your own choice. Let \(s_0\) be the length of a side in a regular hexagon, \(s_1\) be the length of a side in a regular dodecahedron, \(s_2\) the length of a side in a regular 24-gon, and so on. Find a recursive formula for \(s_n\).
3. Use the recursive formula obtained and a spreadsheet to approximate \(\pi\). It’s easier to use the circumference than the area (since you, unlike Liu Hui, can use clever numerals and a computer).
4. Use relative copies to obtain better approximations of \(\pi \). Show 15 decimals by choosing Option->Rounding->15 Decimal Places. After a number of steps, GeoGebra recognizes that the number in question is \(\pi \). What happens after these steps and why?

And then what?

The reason Liu Hui used areas instead of circumferences was that he found a clever way of approximating the area of a polygon with a rational number, thus avoiding having to taking successive square roots.

There is no known record of any approximation of \(\pi\) prior to Archimedes. Those claiming there is, do not refer to any known references where any significant property of \(\pi \) is mentioned.

Archimedes used rational numbers as approximation of square roots. He approximated \(\sqrt{3}\) correct to 5 significant figures. There is no record of how he did it.

Archimedes (≈250 BC) used a 96-gon.

Liu Hui (≈250 AD) used a 3072-gon.

Zu Chongzhi (≈500 AD) used a 12 288-gon to obtain \(\pi\approx 3.1415962\), correct to 8 significant figures.

↓ 900 years later

Madhava of Sanganagrama (≈1400 AD) obtained 10 correct significant figures by using a series later called the Leibniz' series.

Leibniz discovered this series ≈1700 AD and proved that ot was correct.

↑ 300 years later 

The Formula, solution

Start with a circle with radius r and a n-gon with a known side \(s_0\).

In the picture to the right, \(OB=OC=r\).

Using Pythagoras' theorem on the triangle \(\Delta OBD\) we get

\[OD=\sqrt{r^2-\frac{s_0^2}{4}}\]

The length

\[CD=r-OD=r-\sqrt{r^2-\frac{s_0^2}{4}}\]

Using Pythagoras' theorem on the triangle \(\Delta BCD\) we get

\[BC=\sqrt{BD^2+CD^2}=\sqrt{\frac{s_0^2}{4}+\left(r-\sqrt{r^2-\frac{s_0^2}{4}}\right)^2} \]

This can be simplified as below.

\[BC=\sqrt{\frac{s_0^2}{4}+r^2-2r\sqrt{r^2-\frac{s_0^2}{4}}+\left(r^2-\frac{s_0^2}{4} \right)} = \sqrt{2r^2-2r\sqrt{r^2-\frac{s_0^2}{4}}}\]

The last simplification is not needed in order to enter it into a spreadsheet.

A hexagon

A regular hexagon can be divided into six equilateral triangles with the interior angles 60°. If the hexagon is inscribed in a circle with radius 1, the side length of the hexagon is 1. We get the recursive formula for the side lengths of the successive polygons

\[ \left\{ \begin{eqnarray} s_0 &=& 1 \\ s_{n+1} &=& \sqrt{2-2\sqrt{1-\frac{s_n^2}{4}}} \end{eqnarray} \right. \]

where \(s_0\) is the side of the hexagon and \(s_n\) is the side of a \(6\cdot 2^n\)-gon when \(n > 1\).