The tiling is made of regular hyperbolic polygons inside a circle \(C_\infty\). The inside of \(C_\infty\) is the hyperbolic universe, which is commonly called the Poincaré disc. The circle itself is not included in the universe but can be seen as the circle at infinity.

For a regular hyperbolic polygon, all angles are equal, and all sides have the same hyperbolic length. Reflecting a polygon in all its edges and then repeatedly reflecting each newly created polygon in its “free” edges create the tiling. The first reflections are shown as arrows in the figure below. Except for algorithmic reasons, the ordering does not matter. Reflecting any of its neighbours can create every polygon.

p and q

In the tiling above, \(p\) is the number of vertices of each polygon, and \(q\) is the number of polygons adjacent to each vertex.

For a Euclidean tiling of regular polygons, the only possible pair of values are: \(p = 3, q = 6 \) or \(p = 4, q = 4\) or \(p = 6, q = 3 \). See Geometry - Tessellations and Symmetries for the Euclidean case. In the Euclidean case, the angle sum of a regular polygon with \(p\) sides is \((p-2)\cdot \pi\). Having \(q\) such polygons meeting at each vertex, following must be true:

\[ \begin{align*} \frac{(p-2)\cdot \pi}{p}\cdot q &= 2\pi \\ \iff \\ (p-2)\cdot q &= 2p \\ \iff \\ p\cdot q-2q-2p+4 & = 4 \\ \iff \\ (p-2)\cdot (q-2) &= 4 \end{align*} \]

In hyperbolic geometry, the angle sum of a triangle is less than \(\pi\) and the angle sum of a regular polygon with \(p\) sides is less than \((p-2)\cdot\pi\). Let \(\alpha\) be the inner angle of a hyperbolic polygon in a pq-tiling, then:

\[ \frac{(p-2)\cdot \pi}{p}\cdot q > \alpha\cdot q = 2\pi \]

For that reason, following relation must hold for any hyperbolic pq-tiling of regular polygons.

\[ (p-2)\cdot (q-2) > 4 \]

Distances

It can be shown that all hyperbolic triangles that are similar, are in fact congruent. This puts a restriction on the distances used when making a hyperbolic tiling of regular polygons.

In Euclidean geometry there are only three possibilities when it comes to the values of \(p\) and \(q\), but there is no restriction on the size of the polygon. In hyperbolic geometry there are infinitely many pairs of \(p\) and \(q\) that can be used for making a tiling of regular polygons, but in any tiling the size of the polygon is uniquely determined by \(p\) and \(q\). There is only one hyperbolic size. In the interactive example above, one point can be moved freely, the other point can only be moved along a hyperbolic circle. From a Euclidean point of view, the distance between the points is smaller when the points are close to the edge of the hyperbolic universe. In the hyperbolic universe however, the distance between the two points is constant.

For a given \(p\) and \(q\), it is easiest to consider a hyperbolic polygon at the centre of the universe when finding the size of all regular polygons of the tiling.

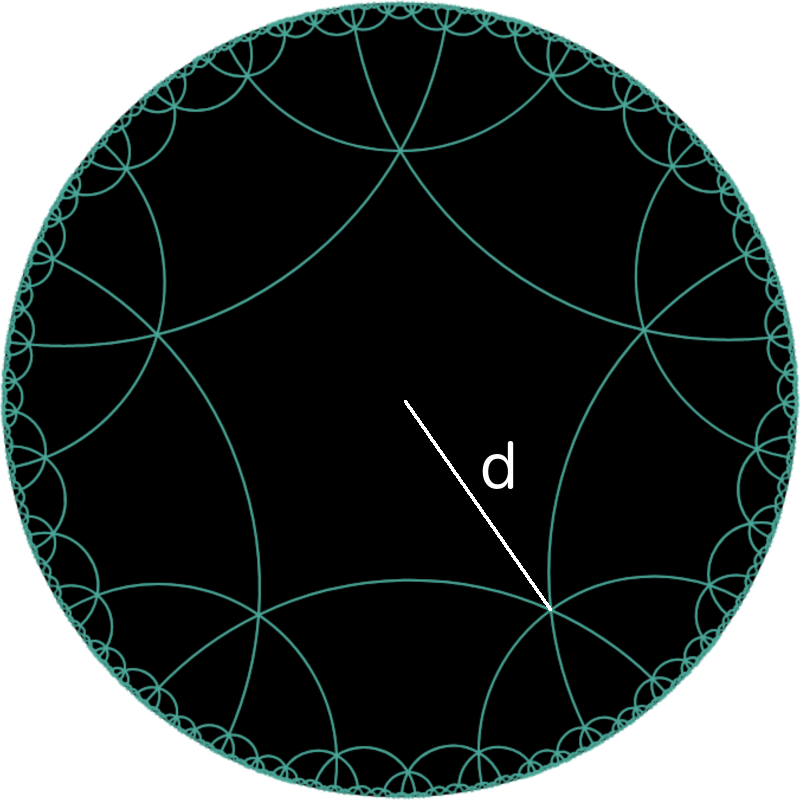
Let \(d\) be the Euclidean distance between a vertex of a centred hyperbolic polygon and the centre of the universe \(C_\infty\). For simplicity, let \(C_\infty \) be a unit circle in the given Euclidean coordinate system, then the distance is given by

\[ d = \sqrt{ \frac{ \tan\left( \frac{\pi}{2}-\frac{\pi}{q} \right)-\tan\left( \frac{\pi}{p} \right) } { \tan\left( \frac{\pi}{2} - \frac{\pi}{q} \right) + \tan\left( \frac{\pi}{p}\right) } } \]

The GeoGebra compatible code for the formula is:

d = sqrt((tan(π / 2 - π / q) - tan(π / p)) / (tan(π / 2 - π / q) + tan(π / p)))

To derive the formula for \(d\) we must first understand what two angles are given by \(p\) and \(q\). An example of the two angles is illustrated below.

Given a red angle and a blue angle, we can se that \(\alpha\) in the figure below is half of the red angle and \(\beta \) is half of the blue angle. Furthermore the positions of \(A\) and \(A'\) depend on \(d\).

In the figure below \(P\) is the midpoint of \(A\) and \(A'\) and hence \(OP = (d + 1/d) /2\). Now we can use triangles \(\bigtriangleup OPM\) and \(\bigtriangleup APM\) to express the height \(h\) in terms of \(\beta\) and \( \gamma \). As a last step we express the angles \(\beta\) and \(\gamma\) in terms of \(P\) and \(Q\). Then we set up an equation which is then solved for \(d\).

When \(d\) has been calculated, any hyperbolic polygon for that tiling can be created by using a hyperbolic compass, as described on the previous page: GeoGebra Constructions in the Poincaré Disc: Exercise 7.

For another example of an interactive tiling, where you can load any image and make a hyperbolic tiling of it, see Make Hyperbolic Tilings of Images.

Completeness of basic hyperbolic constructions

Although we will not need a hyperbolic rotate tool, for the sake of completeness we will show the instruction for making one.

Construct a hyperbolic rotate tool

The GeoGebra-tool Rotate Object around Point by Angle doesn't really rotate an object but creates a copy of an object that is rotated relative to original object. We can make a hyperbolic version of the rotate-tool that creates a geodesic that is rotated around a point.

• Make two points A and B with distances to the origin less than one. Construct the inverted points A' and B':
  A'=Reflect[A, Circle[(0, 0), 1]]
B'=Reflect[B, Circle[(0, 0), 1]]
• Use the tool HypLine on A and B to create a hyperbolic line hline.
• Make the centre M of hline: M = Centre[hline]
• Make a line a through A and M.
• Make a slider α measuring angles.
• Rotate a to a' around A: a' = Rotate[a, α, A]
• Make the perpendicular bisector b between A and A': b = PerpendicularBisector[A, A']
• Make the intersection C between b and a'.
• Make the circle c through C and A: c = Circle[C, A]
• Make the intersection points between c and the unit circle: Intersect[c, Circle[(0, 0), 1]]
  Rename the intersection points to K_1 and K_2.
• Make a circumcircular arc through K_1, A, and K_2, call it hrotate.
  Hide the label hrotate.
• Create a tool HypRotate that has hrotate as output object and B, α, A as input objects.

Exercises

When making the hyperbolic constructions you will need hyperbolic tools for making a: line, segment, ray, distance, and circle. You can either make them yourself by following the instructions on GeoGebra constructions in the Poincaré disc or copy the activity Basic hyperbolic tools.

You will also need the hyperbolic tools HypPerpendicularBisector and HypCompass described in GeoGebra constructions in the Poincaré disc: Exercise 3 and Exercise 7

Exercise 1

GeoGebra-construction of hyperbolic tiling with centred polygon

1. Make two sliders p and q taking integer values greater than or equal to three.
   Construct the hyperbolic distance d by copying the formula. If you change the values of p and q, d is shown as undefined in the algebra view for some cases. For what values of p and q is d undefined?
2. Make a point O at the origin and a unit circle called unit.
   Make a circle c with O as its centre and d as radius, then make a point A on c. You can find the angle A makes with the positive \(x\)-axis by using the function atan2. To make the angle a, input
   a = atan2(y(A),x(A)).
   Drag A along c and change p and q to make sure your construction is correct.
3. You must now make p evenly spaced points on c. One of them should be the point A. For this it is easiest to use the spreadsheet.
   Start by filling column A with 1, 2, 3, ... up to and including the maximum value of p.
   Write a in B1. Then make the rest of the angles in column B by writing If(A2 ≤ p, B1 + 2 pi/p), and make relative copies along the column.
   Fill in the evenly spaced points on circle c in column C by using basic trigonometry.
   Hide the point C1 so you can drag A. Check that your construction works for various values of p.
4. Column D will be filled by the hyperbolic segments forming the hyperbolic polygon. The first segment will be between C1 and C2. A relative copy of this will work for all segments but the last. The last segment must be between the last defined value in column C and C1. In order to achieve this, write
   If(A1 < p, HypSegment(C1, C2), HypSegment(C1, $C$1))
   and make relative copies along column D.
5. To make a tiling "manually", the vertices in column C must by reflected (by hyperbolic reflection) in one of the segments of the polygon. Then HypSegment can be used to make the reflected polygon. This procedure can be repeated. Note that p and q cannot be changed after making some reflections.

   

   To fill out the tiling with many hyperbolic polygons, programming is preferable.

Exercise 2

GeoGebra-construction of interactive hyperbolic tiling

The tiling in Exercise 1 has one polygon with the origin as its centre. We are now going to make a similar construction but where one polygon can be moved inside the Poincaré disc.

Start by making following objects

• Make a point O at the origin and a unit circle called unit.
• Make a distance d by using the formula.
• Make a circle c with O as its centre and d as radius and put a point A on c.
• Make a point B anywhere inside the unit circle. B will be the centre of the first polygon.
• Use HypCompass to copy c to a circle e having B as centre. Then hide A which will not be used from now on.
• Place a point C on circle e.
• Make the hyperbolic bisector f between B and O, then reflect C in f to a point C'.

Now you can use the method sketched out in Exercise 1 to make the vertices of a hyperbolic polygon on circle c, such that one of the vertices is C'. Then reflect all vertices in the hyperbolic perpendicular bisector f and make the polygon segments between the reflected points. Hide all auxiliary objects and make reflected polygons to make a part of a tiling.

Load GeoGebra worksheet