Ruler and Compass
GeoGebra tasks
| Allowed tools |
|---|
 New Point |
 Intersect Two Objects |
 Line through Two Points |
 Segment between Two Points |
 Ray through Two Points |
 Circle with Centre through Point |
 Compasses |
Construction 1 Bisect angle
Start with: Two rays with a common endpoint.
Construct: A ray dividing the angle between the rays in two equally large angles, such a ray is called an angle bisector; dividing into two equal parts is called bisecting.
Construction 2 Bisect segment
Start with: A segment.
Construct: The midpoint.
Construction 3 Perpendicular line 1
Start with: A line and a point on the line.
Construct: A line through the point perpendicular to the given line, a so called normal line.
Construction 4 Perpendicular line 2
Start with: A line and a point not lying on the line.
Construct: A line through the point perpendicular to the given line.
Construction 5 Reflect point in line
Start with: A line and a point.
Construct: The mirror image of the point when reflected
in the line. Show the traces of the original point and the mirror image
of the point by right-clicking on each point and choose Trace
on. (Use the construction of Perpendicular line 2.)
Construction 6 Parallel line
Start with: A line and a point not on the line.
Construct: A line through the point parallel to the given line. (Use the construction of Perpendicular line 2.)
Construction 7 Multiple of a segment
Start with: A segment.
Construct: A segment who's length is a multiple of the length of the given segment. (For example three times as long.)
In addition to the previous tools you can now also use:
| More allowed tools |
|---|
 Midpoint or Centre |
 Perpendicular Bisector |
 Perpendicular Line |
 Angle Bisector |
 Parallel Line |
 Reflect Object in Line |
Construction 8 Copy circle
Start with: A circle c and a point P.
Construct: A new circle having the same radius as the circle c and having the centre P.
You can use the construction above to copy a segment of a given length. You can now use these tools as well:
| Even more allowed tools |
|---|
 Circle with Centre and Radius |
 Segment with Given Length from Point |
Construction 9 Copy angle
Start with: Two rays a and b with a common endpoint P, and a ray c having another endpoint Q.
Construct: A ray d with the endpoint Q such that the angle between c and d is equal to the angle between a and b.
Construction 10 Dividing a segment into three equal parts (trisecting)
Start with: A segment.
Construct: Trisect the segment.
Hint: Start the construction as below.
Comment: The task of trisecting an angle would have been just a tad more difficult.
Proofs
Use the three congruence theorems, the theorem about isosceles triangles and the theorems about angles to prove that the constructions 1-7 are correct.
Hint: Place triangles in appropriate ways into the constructions.
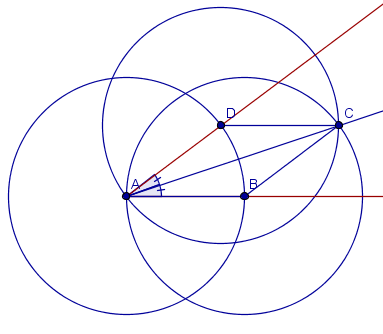
Example, Construction 1 Bisect angle
You must show that the angles BAC and CAD are equal.
Mark the triangles ΔABC and ΔACD.
Use one of the congruence theorems to show that the triangles are congruent. Justify that you can use this theorem.
Show that the angles BAC and CAD are equal.
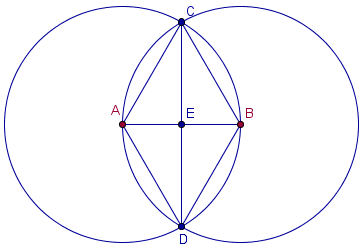
Example, Construction 2 Bisect segment
You must show that the segments AE and EB are equal.
Show this for the angles: DAB=DBA=CAB=CBA.
Then show this for the angles: BDC=ADC=ACD=BCD .
Show that ΔAED≅ΔBED!
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License