Similar Triangles
Definition
Two triangles are similar if corresponding angles are congruent and if the ratio of corresponding sides is constant. If the triangles \(\bigtriangleup ABC\) and \(\bigtriangleup DEF\) are similar, we can write this relation as
\[\bigtriangleup ABC∼\bigtriangleup DEF.\]The difference between similar and congruent triangles is that similar triangles do not have to be the same size.
\(\cong\) congruence same shape & same size
\(\sim\) similarity same shape
Triangle Proportionality Theorem
A transversal is a line that intersects two or several lines.
Theorem: A transversal that is parallel to one of the sides in a triangle divides the other two sides proportionally.
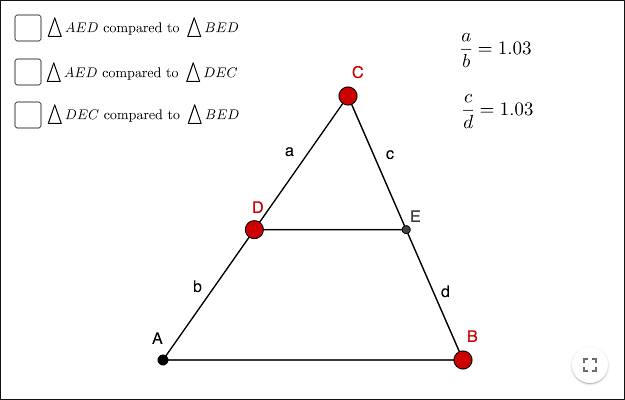
Proof: All you need to know in order to prove the theorem is that the area of a triangle is given by \[A=\frac{w\cdot h}{2}\]
where \(w\) is the width and \(h\) is the height of the triangle. Compare areas three times!
Make a triangle \(poly1=\bigtriangleup AED\) and a triangle \(poly2=\bigtriangleup BED\). Let \(poly1\) and \(poly2\) denote the areas of the triangles. What is the ratio of \(poly1\) and \(poly2\)? Prove your answer!
Make a triangle \(poly3=\bigtriangleup DEC\). What is the ratio of \(poly3\) and \(poly1\)? Prove your answer!
What is the ratio of \(poly3\) and \(poly2\)? Prove your answer!
Show that \(\dfrac{a}{b}=\dfrac{c}{d}\)!
Corollary of Proportionality Theorem
Corollary: A transversal that is parallel to a side in a triangle defines a new smaller triangle that is similar to the original triangle.
Proof:
Show that corresponding angles in the two triangles are congruent (equal).
Then show that \[\frac{a+b}{a}=\frac{c+d}{c}\]
Draw another transversal parallel to another side
and show that \[\frac{a+b}{a}=\frac{c+d}{c}=\frac{AB}{DE}\]
Three cases that yield similarity
Side-Angle-Side (SAS) If two sides in a triangle are in the same ratio to two corresponding sides of another triangle, and if the included angles in both triangles are the same, then the triangles are similar.
Proof
Place the point \(G\) such that \(AG=DE\).
Draw \(GH\) such that \(GH\) is parallel to \(BC\).
Now \(\bigtriangleup AGH∼\bigtriangleup ABC\).
Show that \(AH=DF\)!
Then the congruence case Side-Angle-Side yields \(\bigtriangleup AGH≅\bigtriangleup DEF\) and the proof is done.
The proofs of the other two cases are similar.
Side-Side-Side (SSS) If three pairs of corresponding sides are in the same ratio then the triangles are similar.
Angle-Angle-Angle (AA) If the angles in a triangle are congruent (equal) to the corresponding angles of another triangle then the triangles are similar.
Also note that it suffices that two angles are equal (why?).
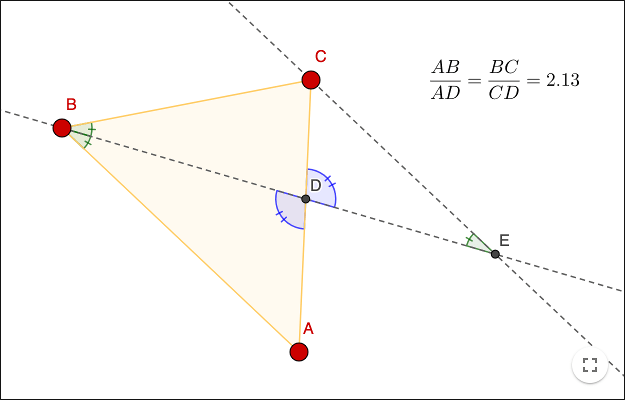
Angle bisector theorem
Theorem: In a triangle \(\bigtriangleup ABC\) an angle bisector is drawn at \(B\). The angle bisector intersects \(AC\) at a point \(D\). The angle bisector theorem states that:
\[\frac{AB}{AD}=\frac{BC}{CD}\]
Proof: Draw a line parallel to \(AB\) through \(C\). Let \(E\) be the intersection of the new line and the angle bisector. Explain why:
\(\angle ABD = \angle CED\)
triangle \(\bigtriangleup BCE\) is an isosceles triangle, and hence why \(BC=CE\).
\(\angle BDA = \angle CDE\)
\(\bigtriangleup ABD \sim \bigtriangleup CED\)
\(\dfrac{AB}{AD}=\dfrac{CE}{CD}\)
\(\dfrac{AB}{AD}=\dfrac{BC}{CD}\)
Exercises
Exercise 1
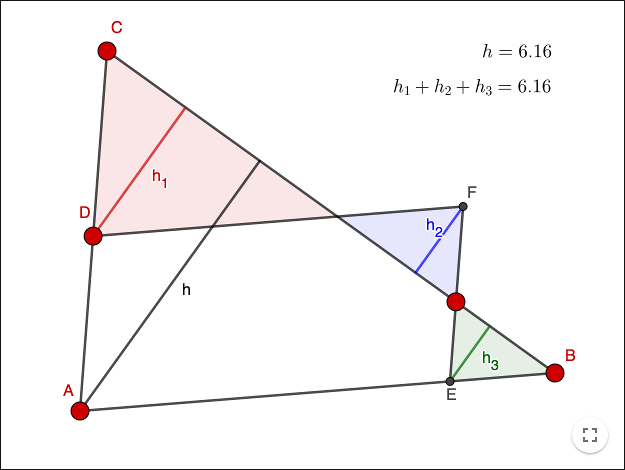
Heights in triangles
\(AC\) is parallel to \(EF\). \(AB\) is parallel to \(DF\). The heights \(h\), \(h_1\), \(h_2\) and \(h_3\) are perpendicular heights in the triangles. Prove what you see!
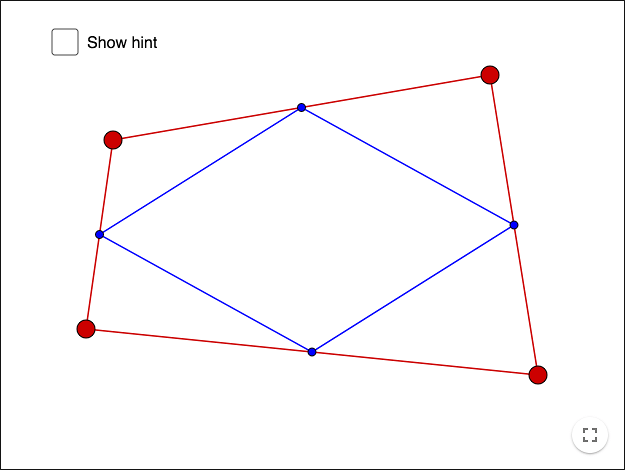
Exercise 2
Midpoints on quadrilateral
The blue points are midpoints on each side. Prove what you see!
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License