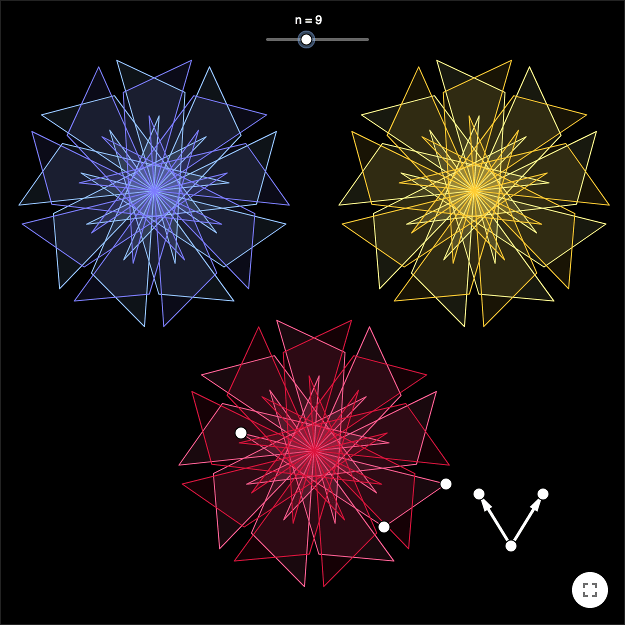
Symmetries

There are three transformations that preserve the size and the shape of an object. If the size and the shape are preserved, then all distances and angles are preserved. Hence, the transformed object will be congruent to the original object. The three transformations are:

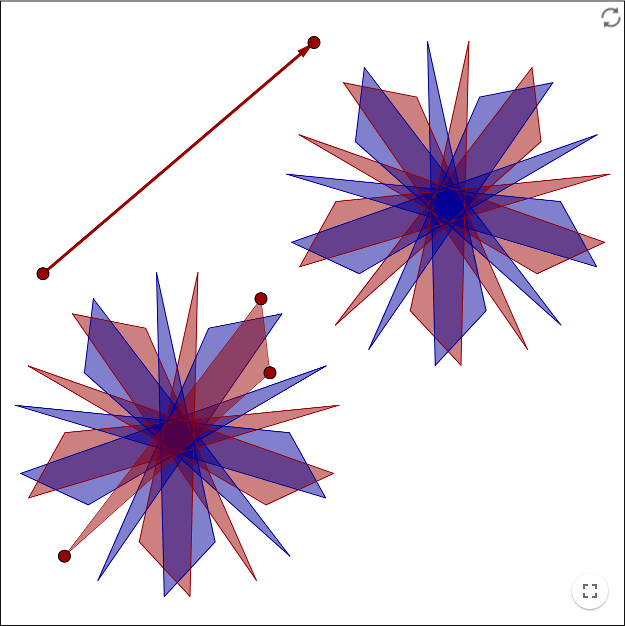
An image is symmetric if you can transform it using one of these transformations in such a way that image is still the same image after the transformation. In that case the image has a reflection symmetry, a rotational symmetry, or a translation symmetry. An image can have several symmetries.

Load GeoGebra worksheet

In order for an image to have a translation symmetry, you must think of the images as if it was extended to infinity. It takes an infinitely large image in order for it to be preserved after a translation. An example of an image having a translation symmetry is a tessellation.

Load GeoGebra worksheet

Using commands

The commands for rotating around a point, reflecting in a line, and translating along a vector, are:

Rotate( <Object>, <Angle>,  <Point> )
Reflect( <Object>, <Line> )
Translate( <Object>, <Vector> )

Commands are especially useful when you want to make many transformations using spreadsheet or lists.

Exercises

Exercise 1

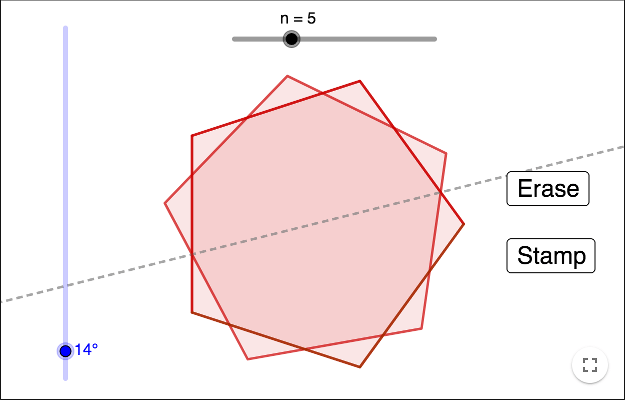
Symmetry lines of regular polygons

Make a slider \(n\) representing the number of vertices.

You can now use the tool Regular polygon to make a polygon having \(n\) vertices. If you use the same two fixed points for all polygons, their sizes will vary too much. Instead do this:

• Make a point \(O\) at the origin and a point \(A\) with the coordinates \((1, 0)\).

• Use the tool Rotate around Point to rotate \(A\) around \(O\) an angle \(\dfrac{360^\circ}{n}\). A point \(A'\) is created.

• Create the polygon using \(A\) and \(A'\).

Now the polygon should be reflected in a line and the user should be able to explore how many symmetry lines a regular polygon has, by noting for which lines the reflected image is the same as the original image.

Create a slider \(\alpha\) of angles and rotate the point \(A\) around \(O\) by the angle \(\alpha\). Name the rotated point \(B\) and make a line \(r\) through \(O\) and \(B\). Reflect the polygon in the line using the tool Reflect about Line.

In order to count the symmetry lines, you can create two buttons Erase and Stamp. Use the tool Button. Enter the GeoGebra Script

ZoomIn(1)

for the Erase button and the script

TraceOn(r, true)
TraceOn(r, false)

for the Stamp button.

Load GeoGebra worksheet

Exercise 2

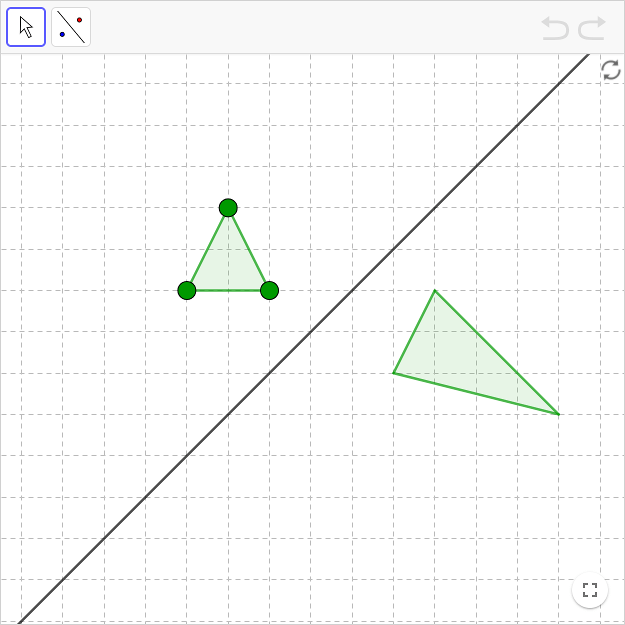
Reflect a triangle in the line \(y=x\)

Reflecting a triangle in a vertical or horizontal line is fairly easy. Reflecting in the line \(y=x\) is somewhat more difficult.

For an exercise where the user should drag the vertices of a triangle to find a "correct triangle", it is best to set the positions of points to "Fixed to Grid" in the styling bar.

Create the line \(y = x\) and any triangle. Hide the points defining the triangle. Select the triangle and check "Fix Object" in the styling bar.

Make another triangle, a triangle with vertices the user can drag.

The task of the user is to make the triangles each other's reflection in the line. And to then check if it was right by using the tool Reflect about Line.

You can choose what tools to use in the menu Tools - > Customize Toolbar.

Load GeoGebra worksheet

Comment: Similar exercises can made where the user should rotate an object \(90^\circ\) or \(180^\circ\) around a point.

Exercise 3

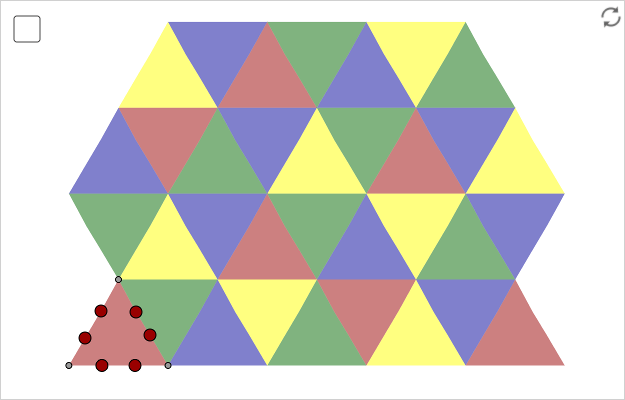
Make a tessellation

• Make a triangle.
• Create a vector \(\vec{u}\) between two of the vertices of the triangle and a vector \(\vec{v}\) using another pair of vertices.
• Use the tool Translate by Vector and make a translated copy using the vector \(\vec{u}\) and a copy using the vector \(\vec{v}\).
• Make several copies of the newly created triangles.
• Drag the points defining the first triangle. The tessellation will change dynamically.
• If you want to color the regions between the triangles, you can make another triangle covering such a region and then make copies using the vectors \(\vec{u}\) and \(\vec{v}\).

Exercise 4

Make rotational symmetry using lists

Create a slider \(n\) for the number of rotations.

Create a triangle and rename it to \(t\).

In order to make \(n\) rotated copies of the triangle, where the rotation is around the origin, write

Sequence(Rotate(t, i*2pi/n), i, 1, n)

Hide the original triangle. Drag the points and change the value of \(n\).

The list you created is one single object. You can choose a color for the list but you cannot let different list elements have different colors. If you want the triangles to have different colors, use the spreadsheet instead.

Load GeoGebra worksheet

Exercise 5

Make a tessellation using lists

Make a regular triangle using the points \((0,0)\) and \((1,0)\). Hide the triangle and see to it that the three points \(A, B, C\) are fix objects (not draggable).

Add another six points placed approximately on the sides of the hidden regular triangle. Make a polygon using these nine points. Rename the polygon to \(p\).

Make two translation vectors \(\vec{u} = \vec{AB}\) and \(\vec{v} = \vec{AC}\).

Create a list using one of the vectors:

Sequence(Translate(p, i*u), i, -5, 5)

A list \(L_1\) is created. Hide it.

Create a list of translated copies of \(L_1\) using the other vector:

Sequence(Translate(L_1, i*v), i, -5, 5)

Hide the vectors and the original polygon. Drag the points.