Paint Circle-Inverted Mondrian!
| ←How to Make a Cubic Bézier Spline | Variations on Pythagoras' Tree→ |
|---|
- Draw in the left pane.
- Choose colour and pen size.
- The rightmost colour can be picked from the colour selector above the canvas.
- The radius of the inversion circle can be changed using the slider above the canvas.
- Hide the geometric construction if it is annoying.
The geometric construction shows how to construct a point inverted in a circle when using a ruler and compass. The static circle shows the circle of inversion.
The pen and the inverted pen are shown in both panes. The pen paints in the left pane and the inverted pen paints in the right pane. The pen has a constant radius. The radius of the inverted pen varies.
As can bee seen by the construction; the location of inverted pen tends to infinity as the pen approaches the origin.
Inversion in circle
If the circle of inversion has radius \(r\) and centre \(O\), then the inverted point \(P'\) of a point \(P\) lies on the line though \(O\) and \(P\). Furthermore:
\[OP\cdot OP' = r^2\]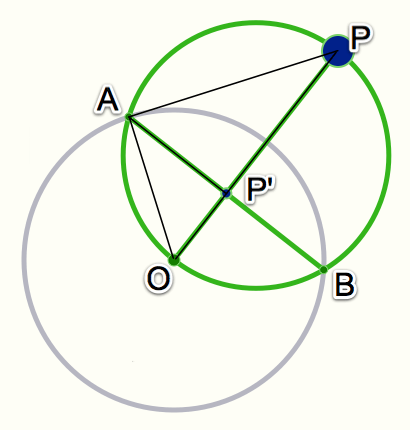
When making a compass and ruler construction, similar triangles are used to show that \(OP\cdot OP' = r^2\).
The small triangle \(\Delta OP'A\) and the large triangle \(\Delta OPA\) share the angle \(\angle AOP\).
The angle \(\angle OAP\) is a right angle due to Thales' theorem. The angle \(\angle OP'A\) is a right angle since \(OP\) and \(AB\) are diagonals of a kite.
Since the triangles \(\Delta OP'A\) and \(\Delta OPA\) share two angles, they are similar.
\[ \frac{OP}{r} = \frac{r}{OP'} \Longleftrightarrow OP\cdot OP' = r^2 \]Drawing fat curves
When the pen moves a small step inside the circle of inversion, the inverted pen moves a larger step. This can be seen when drawing fast inside the circle, before releasing the mouse button. In order to get a smooth curve, the paths of the borders of the pen and the inverted pen are drawn using a Bézier spline, after the mouse button has been released.
Beziér splines are explained at the previous page How to Make a Cubic Bézier Spline.
Processing-code to draw a fat curve can be seen here: Draw a fat curve!.

