Quadrilaterals & Triangles
Quadrilaterals
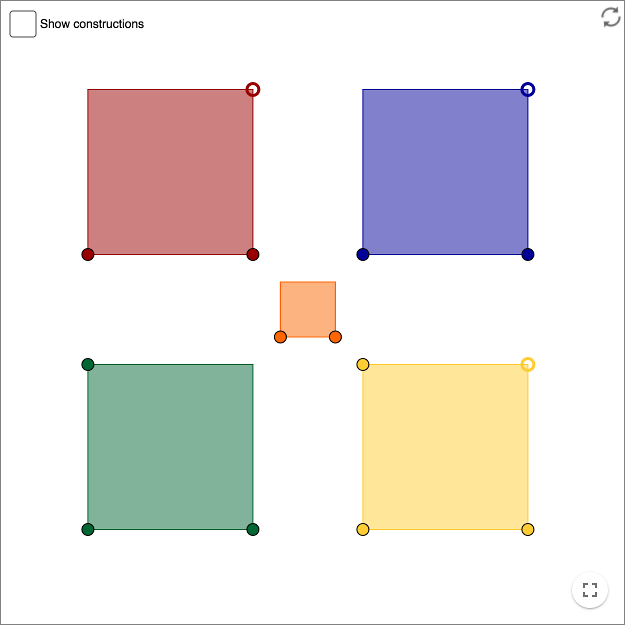
The red quadrilateral is a rectangle, the blue a rhombus, the green a parallelogram,the yellow a trapezium, and the orange small quadrilateral is a square.
A square is a quadrilateral for which all sides have the same length and where adjacent sides are perpendicular to each other.
Exercise 1
Drag the points in the worksheet above. Use one or several of the concepts: parallel, perpendicular, same length - to describe a rectangle, a rhombus, a parallelogram, and a trapezium.
Exercise 2
Can you always place the rectangle on the square and make sure that it has the same shape as the square?
Can you always place the square on the rectangle and make sure that it has the same shape as the rectangle?
Which of the following statements is true?
Exercise 3
Which of the following statements are true?
Triangles
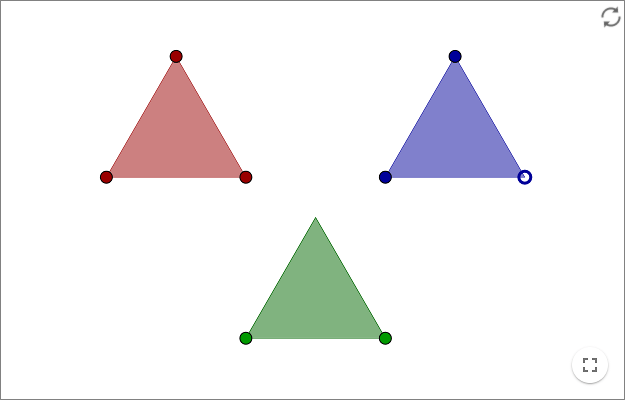
The blue triangle is isosceles and the green triangle is equilateral.
Exercise 4
Drag the points in the worksheet above. Describe in detail what features the isosceles and the equilateral triangles have.
Exercise 5
Which of the following statements is true?
further info:
"Down with Euclid! Death to Triangles!" was a slogan
used by Jean
Dieudonné at a conference in 1959; he argued that geometry
in general and triangles in particular were not needed in real life.
Dieudonné was one of the founding members of Bourbaki.
Bourbaki had a deep influence over the so called New
Math.
New Math has been criticized by among others Morris
Kline.
Some decades later the method of polygon triangulation, i.e. how to divide a polygon into triangles, is important in computer science and the unit "million triangles per second" is used to measure performance of graphics processors, see Comparison of AMD graphics processing units.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License