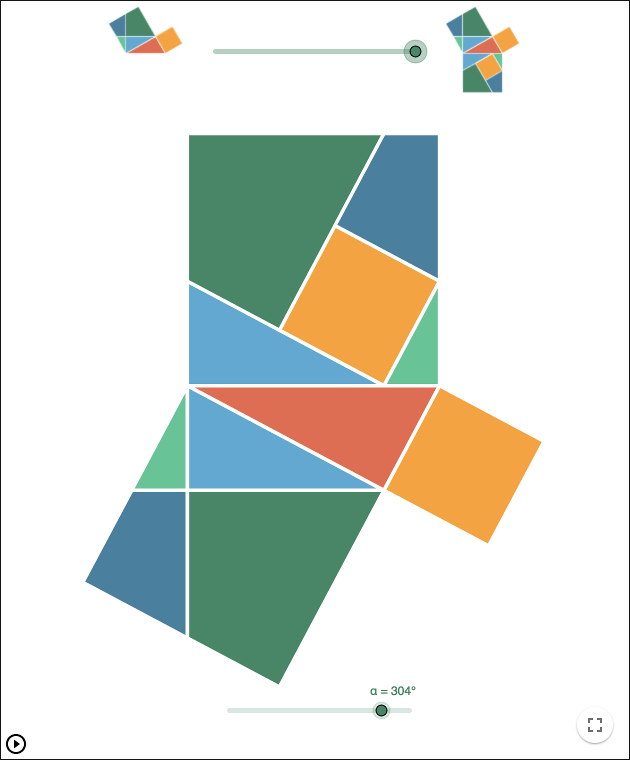Pythagoras & Thales

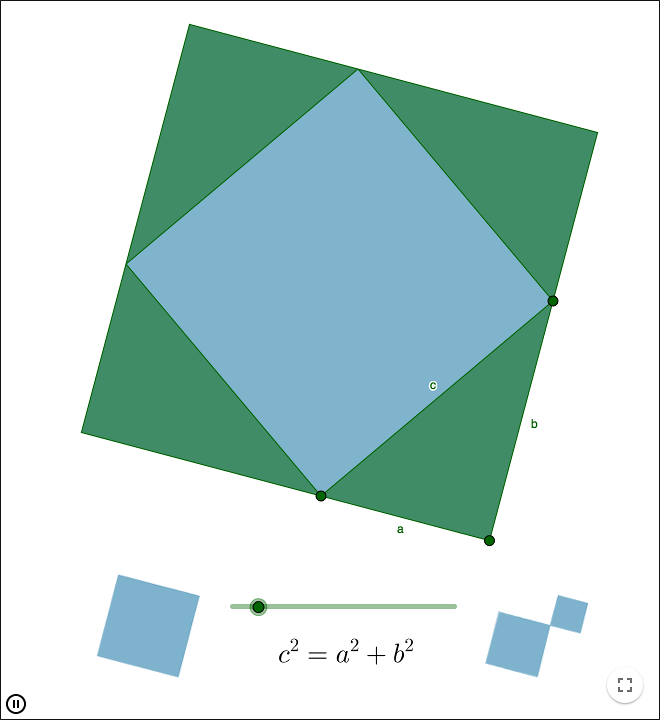
The Pythagorean theorem

Load GeoGebra worksheet

For a right-angled triangle with shorter sides a and b, and the hypotenuse c, following holds:

\[c^2=a^2+b^2\]

Conversely, if three positive numbers a, b, c satisfy \(c^2=a^2+b^2\); then the numbers can be the lengths of the sides of a right-angled triangle.

There are many proofs of the Pythagorean theorem that are based on interpreting the square of a number as the area of a square. You then prove that the area of the two smaller squares in the image below, have the same total area as the large square.

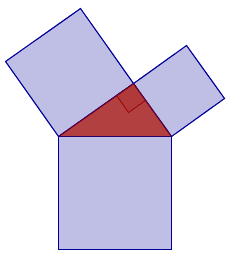
One of the easiest proofs is shown in the worksheet above. A more difficult proof where the smaller squares are cut and then put together as a larger square is shown below.

Load GeoGebra worksheet

Thales' theorem

One easy way to construct a right-angled triangle, is to use Thales' theorem. Thales theorem states that if one of the sides of a triangle is along the diameter of a circle, and if the third vertex also lies on the circle, then the angle at the third vertex is a right angle.

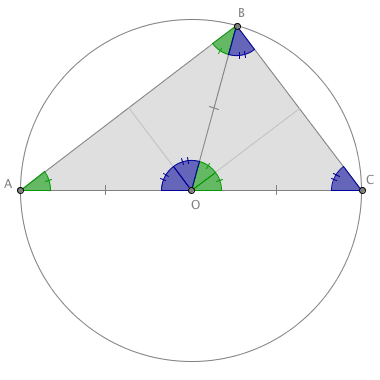
Exercise 1

Use the picture above to prove Thales' theorem!

Dynamic Pythagoras' tree

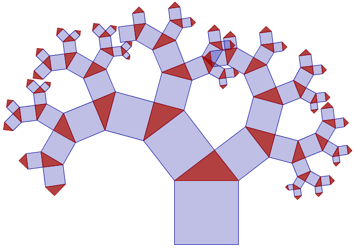
By using Thales theorem, it is possible to make a dynamic variant of a fractal called Pythagoras tree.

Exercise 2

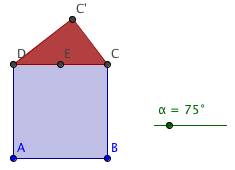
• Input two points \(A\) and \(B\) and a slider \(\alpha\) representing an angle. Use the tool Regular Polygon to make a square as in the picture above.
• Use the tool Midpoint or Centre to make the midpoint \(E\) between \(C\) and \(D\). Use the tool Rotate, to rotate \(C\) around \(E\) by the angle \(\alpha\). Move the slider to see the point \(C'\) move. Make a triangle as in the picture above. The triangle will be a right-angled triangle due to Thales' theorem.
• Pick Tools -> Create New Tool. Make a tool that has the objects \(C\), \(C'\), \(D\), and the two polygons as output objects. The tool will have \(A\), \(B\), and \(\alpha\) as input objects.
• Build a tree by using the tool. Start by clicking two points, then enter α in the input box that shows up.

You can make variations of Pythagoras' tree. For some examples see Variations on Pythagoras' Tree.