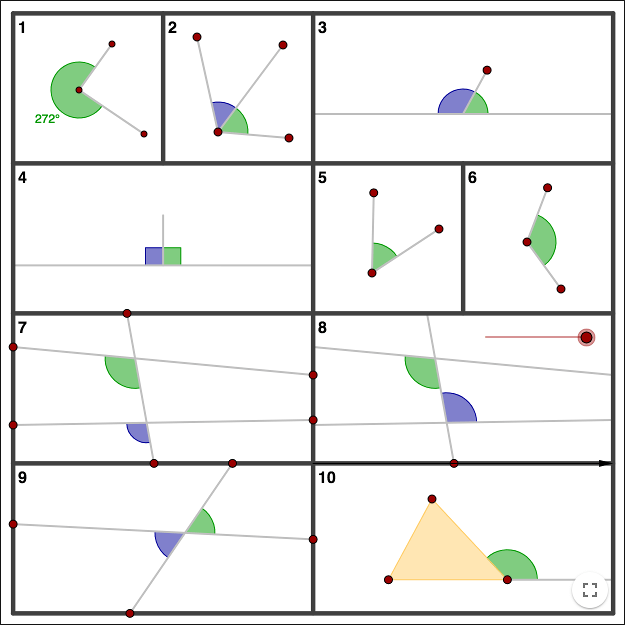
Summary - Angles

Definitions

Load GeoGebra worksheet

1. The angle of one revolution is 360°.
2. Two angles sharing a common ray are called adjacent.
3. Two adjacent angles lying along a line are called supplementary angles.
4. If two supplementary angles are equal they are right angles.
5. An angle that is smaller than one right angle is an acute angle.
6. An angle that is larger than one right angle and smaller than two right angles is an obtuse angle.
7. A line intersecting two other lines is called a transversal. The angles are corresponding angles.
8. The angles are alternate angles.
9. The angles are vertical angles.
10. The angle is an exterior angle to the triangle.

Note: Number 1 has been added to the list even though degrees are not mentioned in the Elements by Euclid.

GeoGebra tasks

Make a line a through the points A and B, and a line b through the points C and D. Enter the point of intersection E and the angle α. Place a point F on the line b.

Task 1

Make an angle β at the point F equal to α , and such that β becomes an alternate angle when a new line is drawn. What can you say about the line a and the new line?

Task 2

Make an angle β at the point F equal to α , and such that β becomes a corresponding angle when a new line is drawn. What can you say about the line a and the new line?

Theorems

Theorem 1 Vertical angles are equal.

Theorem 2 In any triangle, the sum of two interior angles is less than two right angles.

Theorem 3 If two lines are intersected by a transversal, and if alternate angles are equal, then the two lines are parallel.

Theorem 4 If two parallel lines are intersected by a transversal, then alternate angles are equal.

Theorem 5 If two lines are intersected by a transversal, and if corresponding angles are equal, then the two lines are parallel.

Theorem 6 If two parallel lines are intersected by a transversal, then corresponding angles are equal.

Theorem 7 - The Exterior Angle Theorem An exterior angle of a triangle is equal to the sum of the two remote interior angles.

Theorem 8 The sum of the interior angles of a triangle is two right angled.

Theorem 9 The converse of the isosceles triangle theorem If two angles in a triangle are equal, then the triangle is isosceles.

Exercises

The theorems you should know by before doing this, are: the congruence cases SAS, SSS, ASA, and the theorem about angles in an isosceles triangle.

Exercise 1

Prove Theorem 1

Exercise 2

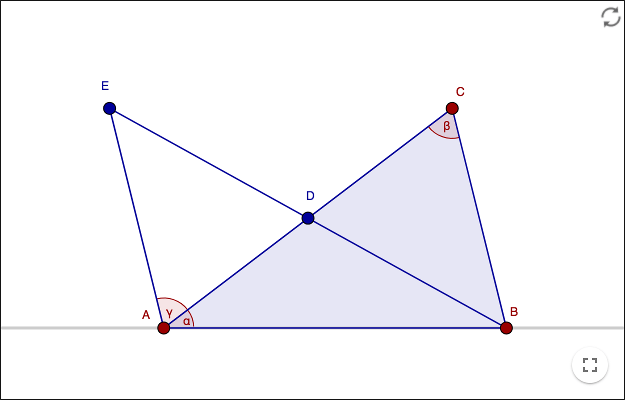
In the demonstration below, D is the midpoint of the segment AC and also the midpoint of the segment BE. As long as the vertices of the triangle have the counterclockwise order A, B, C; the sum of α and γ is less than two right angles. Show that γ=β. Then prove Theorem 2. You are only allowed to use theorems that have already been proved.

Load GeoGebra worksheet

Exercise 3

Prove Theorem 3. Try to do a proof by contradiction, i.e. assume that your proposition is not true; then show that this assumption leads to a contradiction. Then use Theorem 3 to prove Theorem 4, a proof by contradiction works in this case as well.

Exercise 4

Use some of the theorems proved so far to prove Theorem 5 and 6.

Exercise 5

Prove Theorem 7 - The Exterior Angle Theorem. Use the picture below. The line l is parallel to AC.

Exercise 6

Prove Theorem 8.

Exercise 7

Prove Theorem 9! Hint: draw an angle bisectris at one of the vertices of the triangle.