Circumscribed and Inscribed Circles

Load GeoGebra worksheet

Bisectors and distances

There are infinitely many ways to measure the distance between a point and a line. For the sake of simplicity, the distance between a point and a line is defined to be the shortest distance, that is the perpendicular distance.

For angle bisectors and perpendicular bisectors, the following is true:

The three perpendicular bisectors of a triangle intersect at one point. The three angle bisectors intersect at another point.

Exercises

The circumscribed circle

Create a triangle.

Given any triangle, it is always possible to find a circle such that all the vertices of the triangle lie on the circle. This is the so-called circumscribed circle.

Use one of the points shown above as the midpoint of the circle. This point is called the circumcenter of the triangle. Explain why the construction works!

The inscribed circle

Given any triangle, it is always possible to find a circle inside the triangle such that the circle is tangent to each of the three sides of the triangle. This is the so-called inscribed circle.

Use one of the points shown above as the midpoint of the circle. This point is called the incenter of the triangle. Use the fact that the inscribed circle must be tangent to the sides of the triangle to construct the circle. Explain why the construction works!

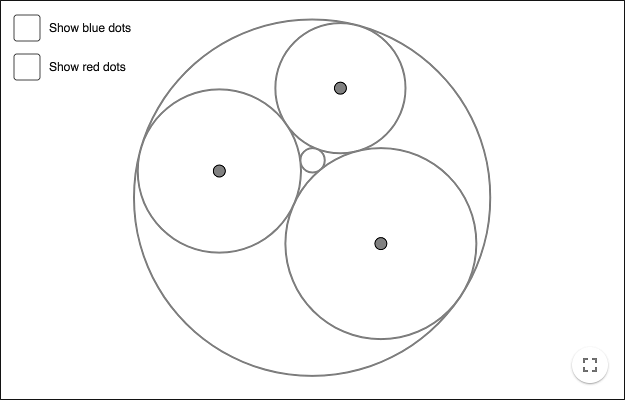
Three circles

Given three points, that are not collinear, it is always possible to construct three circles that are mutually externally tangent to each other. Two circles are externally tangent, if they have a tangent in common and lie on opposite sides of this tangent.

Use the construction of the inscribed circle to construct three circles tangent to each other. Explain why the construction works!

Soddy circles

Given three circles that are mutually externally tangent to each other, it is always possible to construct two new circles that are tangent to each of the three circles. These two new circles are so-called Soddy circles. This is a special case of circles of Apollonius.

Start with a triangle and three tangent circles.

Draw perpendicular lines from the midpoints of the circles, lines that are perpendicular to the opposite triangle side. Each such line intersects its circle in two point, create these intersection points. These intersection points are blue in the picture below. Make six such points, two per circle.

Make the intersection points of the circles, the points of tangency. Each circle has an opposite point of tangency. These points are yellow in the picture below.

Each circle has two blue points. For each circle, draw two lines between each blue point and the opposite point of tangency. These lines are red for one of the circles in the picture below.

The red lines intersect its circle in one new point each. Create these intersection points. These intersection points are red in the picture below. Create six red points, two per circle.

Use the tool Circle through Three Points to construct the two Soddy circles using the red points.

Extra Exercises

Exercise 1

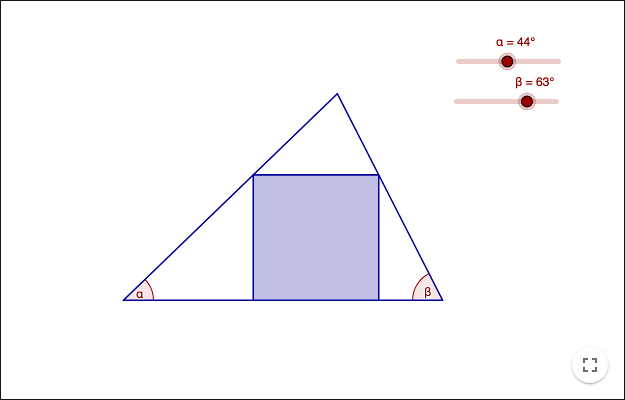
A square inscribed in a triangle

Given an acute triangle you can always find a square having its vertices on the sides of the triangle. Construct this square.

Load GeoGebra worksheet

Solve the problem in following steps:

Is there an easy way of inserting a square in a triangle such that two of the vertices lie on sides of the triangle?

Is there an easy way of inserting a square in a triangle such that three of the vertices lie on sides of the triangle?

In what way does the fourth vertex move when the square is altered? Find the pattern! Make a conjecture about the position of the fourth vertex.

Exercise 2

Napoleon's Theorem

Start with: A triangle ΔABC.

Construct: Three regular triangles along the sides of the original triangle, the regular triangles should point outwards. Find the centers of the three regular triangles (The centers are the midpoints of the circumscribed circles, the so-called circumcenter) Make a new triangles through the centers. Make a conjecture about the new triangle.