Aristarchus ≈ 250 BC, the size of the sun
In various cultures throughout history, the ratio between sides of a triangle has been used to measure distances. Some of these distances have had a major impact on science and on our conception of the world.
The sun, earth and moon
The sun and the moon appear to have the same size.
That observation was made by Aristarchus when he observed a solar eclipse. He also realized that they do not have to be equal in size if only the sun is further away than the moon.
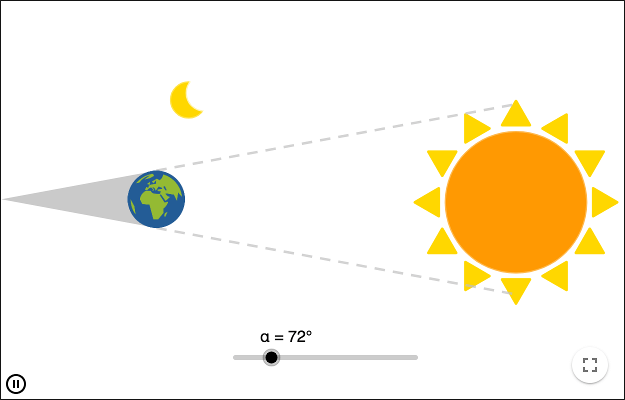
Let \(d\) be the distance to the moon and \(D\) the distance to the sun. Let \(r\) be the radius of the moon and \(R\) the radius of the sun. If the angular sizes of the moon and the sun are equal, the triangles are similar.
Aristarchus wanted to compare the sizes of the sun and the earth.
Exercise 1
Find the ratio of \(R\) and \(r\) in terms of \(D\) and \(d\)!
Exercise 2
Aristarchus knew what the moon looked like when the angle \(\beta\) was \(90^\circ\). (What does it look like?). He then estimated the angle \(\alpha\).
Aristarchus estimated the angle \(\alpha\) to \(87^\circ\). During a lunar eclipse he estimated that the radius of the moon was about one third of the radius of the earth. Using these numbers, calculate the ratio of the radius of the sun and the radius of the earth! Using these numbers, how much larger is the sun than the earth (Now it is a comparison of volumes, not radii)?
Aristarchus then concluded:
The giant sun does not
move around the tiny earth,
it is probably the
other way around!
Exercise 3
Aristarchus made a minor mistake when comparing the radius of the earth with the radius of the moon, otherwise his method was correct.
The data used by Aristarchus, on the other hand, was not correct. Aristarchus' estimation of the angle \(\alpha\) was \(87^\circ\), the modern estimation is \(87^\circ50'\)', i.e. \(89 + \dfrac{50}{60}\) degrees. Find the ratio \(D:d\) using the correct angle! What was his relative error when measuring the angles? What is the relative error in distances? What is the relative error in volumes?
A modern comparison of volumes is: 1 sun ≈ 1 300 000 earths

It might be easier to remember that:
1000 earths ≈ 1 Jupiter
1000 Jupiters ≈ 1 sun
references:
A discussion about calculations and mistakes made by Aristarchus: Aristarchus's On the Sizes and Distances of the Sun and the Moon: Greek and Arabic Texts, by J.L Berggren and Nathan Sidoli (pdf)
Globe-icon from: Free Icons Library: Glove Icon SVG #399087.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License