Apollonian Gasket

Since angles are preserved under inversion in circle (see Non-Euclidean Geometry ‐ Inversion in Circle), tangency is also preserved. Starting with five tangent circles, you can make a pattern like the Apollonian gasket by repeatedly invert in circles.

Start with five circles such that each circle is tangent to at least three of the others (see Geometry - Circumscribed and Inscribed Circles). There are six places where one can make a new circle (the gray regions in the picture below). The new circle should be tangent to three of the original circles. For each such new circle there will be three new regions where one can make new circles. The process can be repeated.

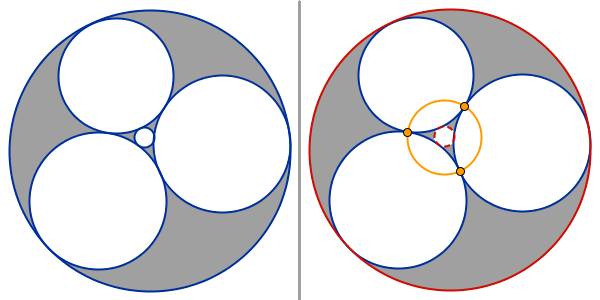
Repeating the procedure of making new circles, that are tangent to three other circles, will produce a circle fractal called an Apollonian gasket.

Geometrical construction of an Apollonian gasket

When making a geometrical construction of an Apollonian gasket, new circles are created from triplets of circles by using circle inversion. To ensure that the tangency is preserved, some properties of tangent circles under circle inversion are used.

Every circle in a triplet of mutually tangent circles should remain unaltered after reflection

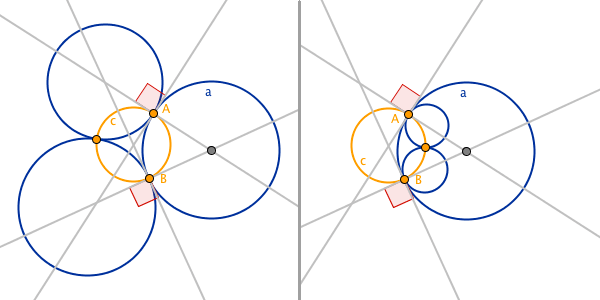
Given three circles that are mutually tangent to each other, make a circle though their intersection points. The circle through intersection points is called c in the picture above. c is the circle used for making new circles through circle inversion.

The picture above depicts what it looks like in the two cases that give rise to three intersection points. Other cases of mutually tangent circles are also possible, but those will only yield one or two intersection points.

Consider what happens when the circle a is reflected in c. The points A and B lie on c, they are therefore not altered when reflected in c. Since circle inversion preserves angles, the right angles at A and B will still be right angles after the reflection. The reflection of a in c, is a circle through the same points A and B. The reflected circle will have tangents at A and B that are perpendicular the tangents of c at A and B. Therefore the reflected circle must be the same as the original circle a.

Tangency is preserved

Create a circle through the intersection points of three mutually tangent circles. The three tangent circles are blue in the picture below. In order to construct a circle tangent to the three circles, note that there already is a circle in the construction that is tangent to them, this is the red circle in the picture below. If the circles a, b, c, d, were reflected in the yellow circle; the reflections of a, b, and c, would be the same circles as a, b, c. Furthermore, the reflection of d would be tangent to all three, since tangency is preserved when reflecting in circles. Hence, by reflecting the red circle d, a new circle is created that is tangent to all three blue circles.

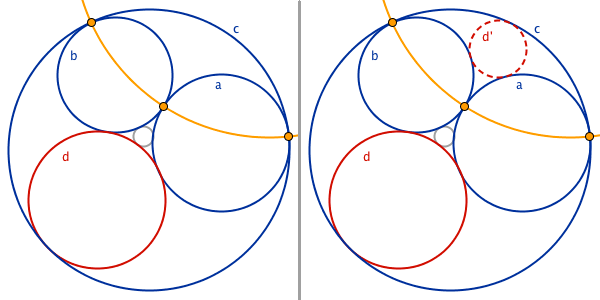
The easiest way to do this in GeoGebra is to use the spreadsheet. The circle through the intersection points, and the reflection that follows, can be made using the commands:

A1=Circle[Intersect[a,b], Intersect[a,c], Intersect[b,c]]
B1=Reflect[d,A1]

The original circles can be renamed to A1,...,A5; they will then automatically appear in the first five cells under column A in the spreadsheet. The circle through the intersection points is not needed, it will not be used again. It is possible to write the above as one single command.

B1=Reflect[d,Circle[Intersect[a,b], Intersect[a,c], Intersect[b,c]]]

Of the six regions that are to be packed by new circles, three lie adjacent to the largest circle, and three are adjacent to the smallest circle. Keep packing circles in the region between the circles a, b, c. If doing it in the spreadsheet, it is easy to copy the code to fill in the other two regions adjacent to the largest circle c.

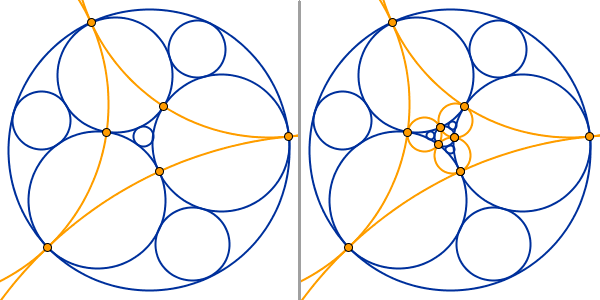
When the outer regions, those that are adjacent to the largest circle, have been filled; all the newly created circles can be reflected to fill the inner regions, those adjacent to the smallest circle.

Apollonian gasket as a limit set

An Apollonian gasket can also be generated as a so-called limit set of a so-called Schottky group made by pairing tangent circles. By slightly changing the circles/Schottky group, the limit set can be made to look like a twisting gasket. Drag the slider to make a twisted Apollonian gasket.