Sammanfattning - Vinklar
Definitioner
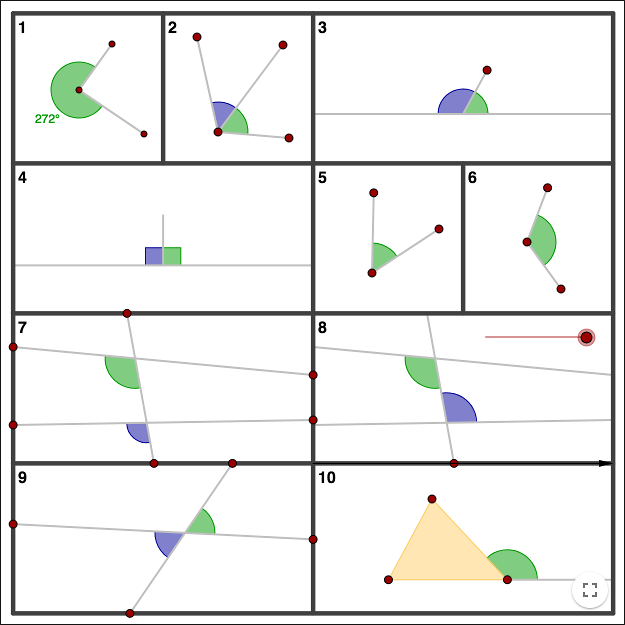
Ändra glidaren för att se olika varianter av likbelägna vinklar och alternatvinklar.
- Ett varv har vinkeln 360°.
- Två vinklar som ligger bredvid varandra och delar ett vinkelben kallas närliggande vinklar.
- Två närliggande vinklar som ligger längs en linje kallas supplementvinklar.
- Om två supplementvinklar är lika kallas de räta.
- En vinkel som är mindre än en rät vinkel kallas spetsig vinkel.
- En vinkel som är större än en rät och mindre än två räta kallas trubbig vinkel.
- En linje som skär två andra linjer kallas transversal. Vinklarna är likbelägna vinklar.
- Vinklarna är alternatvinklar.
- Vinklarna är vertikalvinklar.
- Vinkeln är en yttervinkel till triangeln.
Observera att: Nummer 1 är med i listan trots att grader inte nämns i Euklides Elementa.
GeoGebra Uppgifter
Gör en linje a genom punkterna A och B, och en linje b genom punkterna C och D. Markera skärningspunkten E och vinkeln α. Placera en punkt F på linjen b.
Uppgift 1
Gör en vinkel β vid punkten F som är lika stor som α och som blir en alternatvinkel då en ny linje dras. Vad kan du säga om linjen a och den nya linjen?
Uppgift 2
Gör en vinkel β vid punkten F som är lika stor som α och som blir en likbelägen vinkel då en ny linje dras. Vad kan du säga om linjen a och den nya linjen?
Satser
Sats 1 Vertikalvinklar är lika stora
Sats 2 I en triangel är summan av två vinklar alltid mindre än två räta.
Sats 3 Om två linjer skärs av en transversal, och om alternatvinklar är lika stora, så är de två linjerna parallella.
Sats 4 Om två parallella linjer skärs av en transversal, så är alternatvinklar lika stora.
Sats 5 Om två linjer skärs av en transversal, och om likbelägna vinklar är lika stora, så är de två linjerna parallella.
Sats 6 Om två parallella linjer skärs av en transversal, så är likbelägna vinklar lika stora.
Sats 7 - Yttervinkelsatsen En yttervinkel till en triangel är lika med summan av de båda inre motstående vinklarna i triangeln.
Sats 8 Summan av vinklarna i en triangel är två räta.
Sats 9 Omvändningen till satsen om likbent triangel Om två vinklar i en triangel är lika så är triangeln likbent.
Övningar
De satser som du bör känna till sedan tidigare är: kongruensfallen SVS, SSS, VSV, samt satsen om vinklar i en likbent triangel.
Övning 1
Bevisa Sats 1
Övning 2
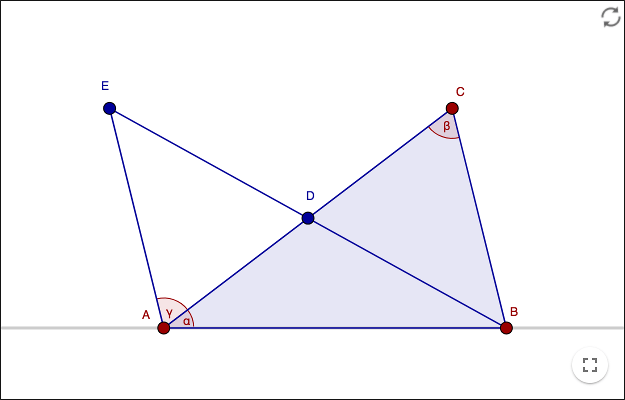
I demonstrationen nedan är D mittpunkt på sträckan AC och på sträckan BE. Så länge triangelns hörn har den moturs orienteringen A, B, C; är summan av α och γ mindre än två räta. Visa att γ=β. Visa sedan Sats 2. Du får bara använda redan bevisade satser.
Övning 3
Bevisa Sats 3. Försök att utföra ett motsatsbevis, dvs antag att det du vill visa inte är sant. Visa sedan att detta antagande leder till en motsägelse. Använd sedan Sats 3 för att visa Sats 4, återigen kan ett motsatsbevis användas.
Övning 4
Använd några av de satser som hittills bevisats för att bevisa Sats 5 och 6.
Övning 5
Bevisa Sats 7 - Yttervinkelsatsen. Använd bilden nedan. Linjen l är parallell med AC.
Övning 6
Bevisa Sats 8.
Övning 7
Bevisa sats 9! Ledning: dra en bisektris vid en av triangelns hörn.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License