Apollonius cirkelfraktal

Eftersom vinklar bevaras vid spegling i cirkel (se Non-Euclidean Geometry ‐ Inversion in Circle), kommer objekt som tangera varandra även att tangera varandra efter spegling i cirkel. Genom att utgå från fem tangerande cirklar, kan man skapa ett mönster som Apollonius cirkelfraktal genom att upprepade gånger spegla i cirklar.

Börja med fem cirklar sådana att varje cirkel tangerar minst tre av de andra (se Geometri - Omskrivna och inskrivna cirklar). Det finns sex ställen där man kan placera en ny cirkel, dessa är grå i bilden nedan. Den nya cirkeln skall tangera tre av de ursprungliga cirklarna. För varje sådan ny cirkel, uppkommer det tre ställen där man kan placera en ny cirkel. Processen kan därför upprepas.

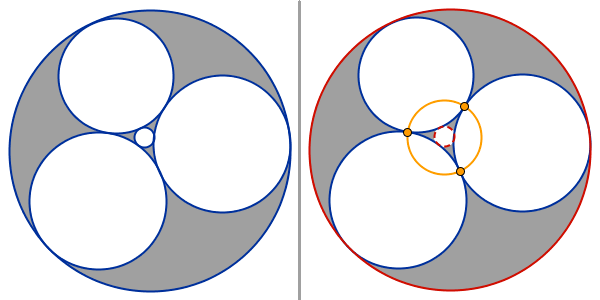
Genom att upprepade gånger göra nya cirklar, som tangerar tre av de gamla cirklarna, får man en fraktal av cirklar som kallas Apollonius cirkelfraktal.

Geometrisk konstruktion av Apollonius cirkel fraktal

Då man gör en geometrisk konstruktion av Apollonius cirkelfraktal, skapar man nya cirklar från tripletter av cirklar genom att använda spegling i cirkel. För att försäkra sig om att alla tangerande cirklar förblir tangerande, används några egenskaper för tangerande cirklar under spegling i cirkel.

Varje cirkel i en triplett av ömsesidigt tangerande cirklar förblir oförändrad efter spegling

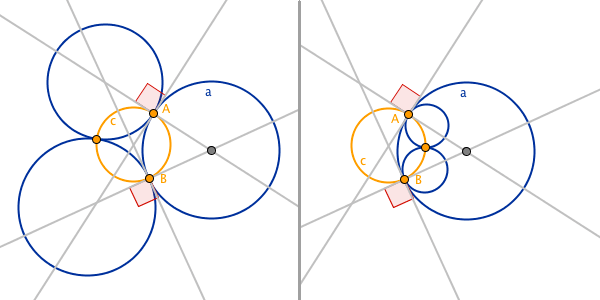
Givet tre ömsesidigt tangerande cirklar. Gör en cirkel genom cirklarnas skärningspunkter. Den nya cirkeln betecknas c i bilden ovan. c används för att göra nya cirklar genom spegling.

Bilden ovan visar bara hur det ser ut i de två fall som ger tre skärningspunkter. Det finns andra fall av ömsesidigt tangerande cirklar, men dessa ger bara upphov till en eller två skärningspunkter.

Punkterna A och B ligger på cirkeln c, de förblir därför oförändrade vid spegling i c. Eftersom spegling i cirkel är an vinkelbevarande operation, kommer de räta vinklarna vid A och B att förbli räta även efter spegling i c. Då a speglas i c, blir resultatet en cirkel som går genom A och B. Den speglade cirkeln kommer att ha tangenter vid A och B som är vinkelräta mot tangenterna till c genom A och B. Därför måste den speglade cirkeln vara samma cirkel som a.

Tangering bevaras

Gör en cirkel genom skärningspunkterna till tre tangerande cirklar. De tre tangerande cirklarna är blå i bilden nedan. För att konstruera en cirkel som tangerar de tre cirklarna, kan man notera att det redan finns en cirkel som tangerar dem, den röda cirkeln i bilden nedan. Om cirklarna a, b, c och d; speglades i den gula cirkeln, så skulle a, b, c förbli oförändrade. Vidare skulle speglingen av d tangera dessa tre, eftersom tangering bevaras vid spegling i cirkel. Man kan därför åstadkomma en nya cirkel som tangerar de tre, genom att spegla den röda cirkeln d i den gula cirkeln.

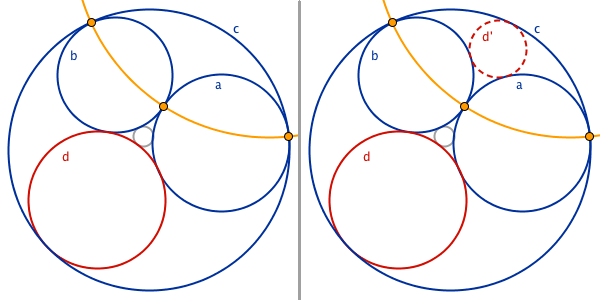
Det enklaste sättet att göra detta i GeoGebra är att använda kalkylbladet. Cirkeln genom skärningspunkterna, och den efterföljande speglingen, kan göras med kommandona:

A1=Cirkel[Skärning[a,b], Skärning[a,c], Skärning[b,c]]
B1=Spegla[d,A1]

De ursprungliga cirklarna kan döpas om till A1,...,A5; de kommer då automatiskt att hamna i de fem översta cellerna i kolonn A i kalkylbladet. Cirkeln genom skärningspunkerna behövs inte, den används inte senare i konstruktionen. Man kan därför skriva koden som ett enda kommando:

B1=Spegla[d,Cirkel[Skärning[a,b], Skärning[a,c], Skärning[b,c]]]

Av de sex områden som skall packas med nya cirklar, ligger tre områden intill den största cirkeln, och tre intill den minsta cirkeln. Fortsätt att packa in cirklar i området mellan cirklarna a, b, c. Om man gör det i kalkylbladet, är det sedan enkelt att göra samma sak i de andra två områden som ligger intill den största cirkeln.

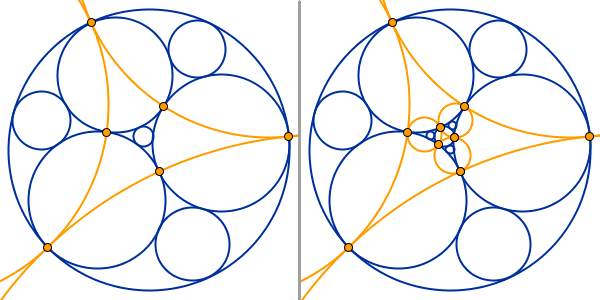
Då de yttre områdena, de som ligger intill den största cirkeln, är färdigpackade; kan de nygjorda cirklarna reflekteras till de tre områden som ligger intill den minsta cirkeln.

Apollonius cirkelfraktal genererad av Möbiustransformationer

Apollonius cirkelfraktal kan också genereras av Möbiustransformationer som tillhör en så kallad Schottky grupp. Genom att förändra transformationerna något, skapas en bild som ser ut som om cirkelfraktalen sträcker på sig. Dra i glidaren för att se fraktalen sträcka på sig.