Likformiga trianglar
Definition
Två trianglar är likformiga om motsvarande vinklar är lika stora och om förhållandet mellan motsvarande sidor är konstant. Att trianglarna \(\bigtriangleup ABC\) och \(\bigtriangleup DEF\) är likformiga skrivs
\[\bigtriangleup ABC\sim \bigtriangleup DEF.\]Skillnaden mellan likformiga och kongruenta trianglar är att likformiga trianglar inte behöver vara lika stora.
\(\cong\) kongruens samma form & samma storlek
\(\sim \) likformighet samma form
Transversalsatsen
En transversal är en linje som skär två eller flera linjer.
Sats: En transversal som är parallell med en av sidorna i en triangel, delar de båda övriga sidorna i samma förhållande.
Bevis: Allt du behöver veta för att utföra beviset är att arean av en triangel ges av \[A=\frac{b\cdot h}{2}\]
där \(b\) är bredden och \(h\) är höjden i triangeln. Jämför tre areor med varandra!
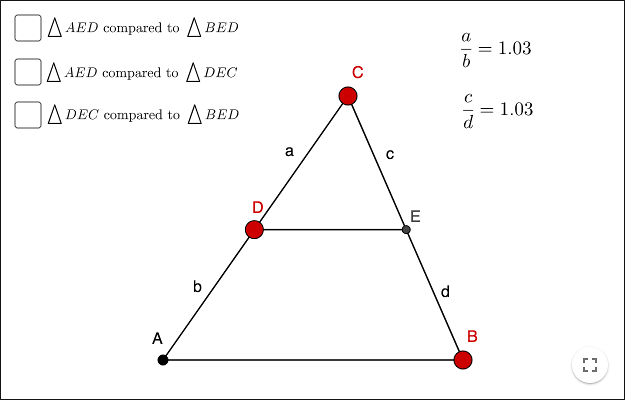
Gör en triangel \(poly1=\bigtriangleup AED\) och en triangel \(poly2=\bigtriangleup BED\). Låt \(poly1\) och \(poly2\) beteckna trianglarnas areor. Vad är förhållandet mellan \(poly1\) och \(poly2\)? Motivera ditt svar!
Gör en triangel \(poly3=\bigtriangleup DEC\). Vad är förhållandet mellan \(poly3\) och \(poly1\)? Motivera ditt svar!
Vad är förhållandet mellan \(poly3\) och \(poly2\)? Motivera ditt svar!
Visa att \(\dfrac{a}{b}=\dfrac{AB}{DE}\)!
Topptriangelsatsen
Som en följdsats till transversalsatsen får man:
Topptriangelsatsen: En transversal som är parallell med en sida i en triangel, avskär en topptriangel som är likformig med den ursprungliga triangeln.
Bevis, Topptriangelsatsen:
Visa först att motsvarande vinklar i de två trianglarna är lika (kongruenta).
Visa sedan att \[\frac{a+b}{a}=\frac{c+d}{c}\]
Drag ännu en parallelltransversal
och visa sedan att \[\frac{a+b}{a}=\frac{c+d}{c}=\frac{AB}{DE}\]
Tre fall som ger likformighet
Första likformighetsfallet, sida-vinkel-sida (SVS) Om två sidor i en triangel är proportionella mot två sidor i en annan triangel och om mellanliggande vinklar är lika stora, så är trianglarna likformiga.
Bevis
Placera punkten \(G\) så att \(AG=DE\).
Drag \(GH\) så att \(GH\) blir parallell med \(BC\).
Nu gäller det att \(\bigtriangleup AGH∼\bigtriangleup ABC\).
Visa att \(AH=DF\)!
Då blir \(\bigtriangleup AGH≅\bigtriangleup DEF\) enligt kongruensfallet sida-vinkel-sida och beviset är klart.
Bevisen för de andra två fallen är snarlika.
Andra likformighetsfallet, sida-sida-sida (SSS) Om de tre sidorna i en triangel är proportionella mot sidorna i en annan triangel så är trianglarna likformiga.
Tredje likformighetsfallet, vinkel-vinkel-vinkel (VV) Om vinklarna
i en triangel är lika med motsvarande vinklar i en annan triangel så
är trianglarna likformiga.
Observera att det räcker att två vinklar är
lika (varför?).
Bisektrissatsen
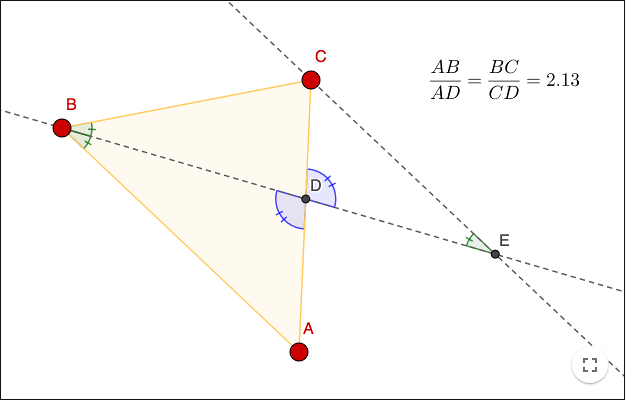
Sats: I triangeln \(\bigtriangleup ABC\) dras en bisektris vid \(B\). Bisektrisen skär \(AC\) vid en punkt \(D\). Enligt bisektrissatsen är:
\[\frac{AB}{AD}=\frac{BC}{CD}\]
Bevis: Dra en linje parallell med \(AB\) genom \(C\). Låt \(E\) vara skärningspunkten mellan den nya linjen och bisektrisen. Förklara varför:
\(\angle ABD = \angle CED\)
triangeln \(\bigtriangleup BCE\) är en likbent triangel, och således varför \(BC=CE\).
\(\angle BDA = \angle CDE\)
\(\bigtriangleup ABD \sim \bigtriangleup CED\)
\(\dfrac{AB}{AD}=\dfrac{CE}{CD}\)
\(\dfrac{AB}{AD}=\dfrac{BC}{CD}\)
Övningar
Övning 1
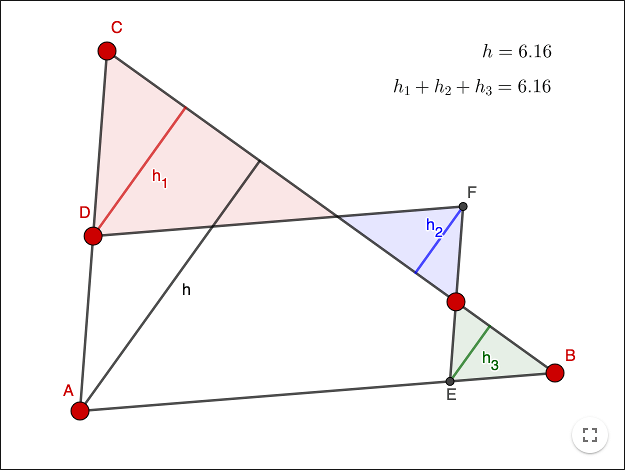
Höjder i trianglar
\(AC\) är parallell med \(EF\). \(AB\) är parallell med \(DF\). Höjderna \(h\), \(h_1\), \(h_2\) och \(h_3\) är de vinkelräta höjderna i respektive triangel. Bevisa det du ser!
Övning 2
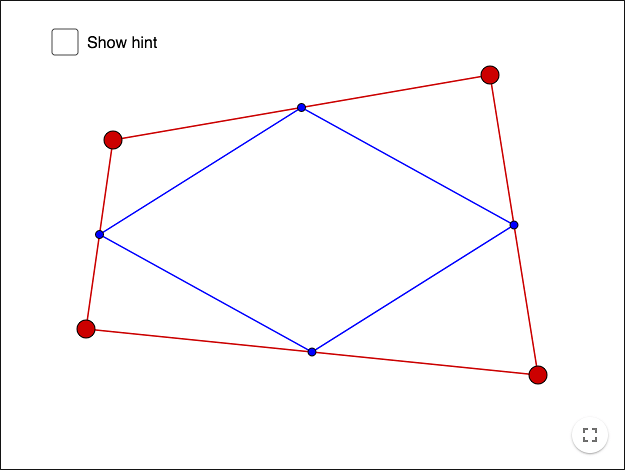
Mittpunkter på fyrhörning
De blå punkterna är mittpunkter på respektive sida. Bevisa det du ser!
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License