Omskrivna och inskrivna cirklar

Ladda GeoGebra-arbetsblad

Mittpunktsnormal, bisektris och avstånd

Det finns oändligt många sätt att mäta avståndet mellan en linje och en punkt. För enkelhetens skull menar man alltid det kortaste avståndet, då man talar om avståndet mellan en punkt och en linje. Det kortaste avståndet är det vinkelräta avståndet.

För bisektriser och mittpunktsnormaler, gäller följande:

De tre bisektriserna till en triangel skär varandra i samma punkt. De tre mittpunktsnormalerna skär varandra i en annan punkt.

Övningar

Den omskrivna cirkeln

Gör en triangel.

Givet en triangel kan man alltid konstruera en cirkel så att triangelns hörn ligger på cirkeln, den så kallade omskrivna cirkeln.

Använd en av de två punkter som beskrivs ovan, som cirkelns mittpunkt. Förklara varför konstruktionen stämmer!

Den inskrivna cirkeln

Givet en triangel kan man alltid konstruera en cirkel inuti triangeln så att cirkeln tangerar triangelns tre sidor, den så kallade inskrivna cirkeln.

Använd en av de två punkter som beskrivs ovan, som cirkelns mittpunkt. Använd det faktum att den inskrivna cirkeln skall tangera triangelns sidor för att konstruera cirkeln. Förklara varför konstruktionen stämmer!

Tre cirklar

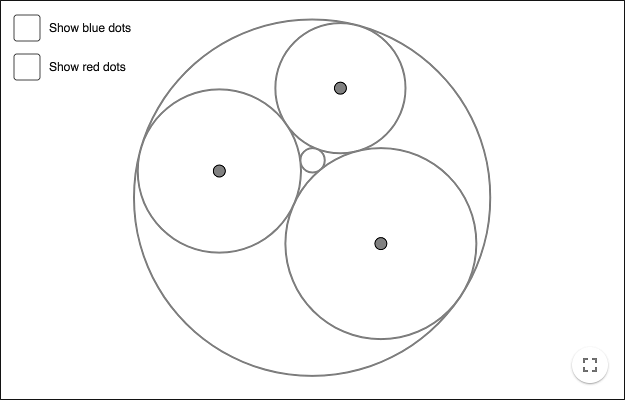
Givet tre punkter, som inte ligger på samma linje, kan man alltid konstruera tre cirklar som ömsesidigt tangerar varandra externt. Två cirklar tangerar varandra externt om de har en gemensam tangent, och om de ligger på varsin sida om denna tangent.

Använd konstruktionen för den inskrivna cirkeln för att konstruera de tre cirklarna. Förklara varför konstruktionen stämmer!

Soddy-cirklar

Givet tre cirklar som ömsesidigt tangerar varandra, kan man alltid konstruera två cirklar som tangerar vardera av de tre cirklarna. Dessa nya cirklar är så kallade Soddy-cirklar. De är ett specialfall av Apollonius-cirklar.

Gör en triangel och tre cirklar som tangerar varandra

Dra vinkelräta linjer från cirklarnas mittpunkter, linjer som är vinkelräta mot motstående triangelsida. Varje sådan linje skär sin cirkel i två punkter, skapa dessa skärningspunkter. Dessa punkter är blå i bilden nedan. Skapa sex sådana punkter, två per cirkel.

Skapa skärningspunkterna mellan cirklarna, tangeringspunkterna. Varje cirkel har en motstående tangeringspunkt. Dessa punkter är gula i bilden nedan.

Varje cirkel har två blå punkter. Drag, för varje cirkel, två linjer mellan vardera blå punkt och motstående tangeringspunkt. Dessa linjer är röda i bilden nedan.

De röda linjerna skär sina respektive cirklar i varsin ny punkt. Skapa dessa skärningspunkter. Dessa punkter är röda i bilden nedan. Skapa sex sådana punkter, två per cirkel.

Använd verktyget Cirkel mellan tre punkter för att skapa Soddy-cirklarna med hjälp av de röda punkterna.

Extraövningar

Övning 1

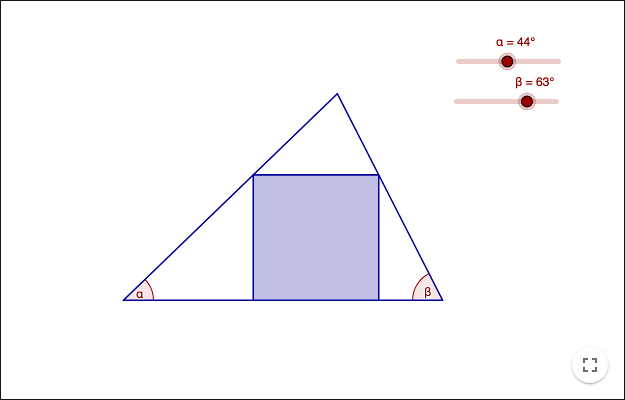
Kvadrat inskriven i en triangel

Givet en spetsvinklig triangel kan man alltid hitta en kvadrat som har alla fyra hörn belägna på triangelns sidor. Konstruera denna kvadrat

Ladda GeoGebra-arbetsblad

Lös problemet i följande steg:

Hur kan man på ett enkelt sätt lägga in en kvadrat i triangeln så att två av hörnen ligger på triangelns sidor?

Hur kan man på ett enkelt sätt lägga in en kvadrat i triangeln så att tre av hörnen ligger på triangelns sidor?

Hur rör sig det fjärde hörnet då man varierar kvadraten? Hitta mönstret! Vad skall gälla för det fjärde hörnet?

Övning 2

Napoleons sats

Utgå från: En triangel ΔABC.

Konstruera: Tre regelbundna trianglar längs de tre triangelsidorna, regelbundna trianglar som pekar utåt. Markera medelpunkten för de tre regelbundna trianglarna (Medelpunkten är de omskrivna cirklarnas medelpunktpunkt) Gör en ny triangel genom de tre medelpunkterna. Vad kan du säga om den nya triangeln?