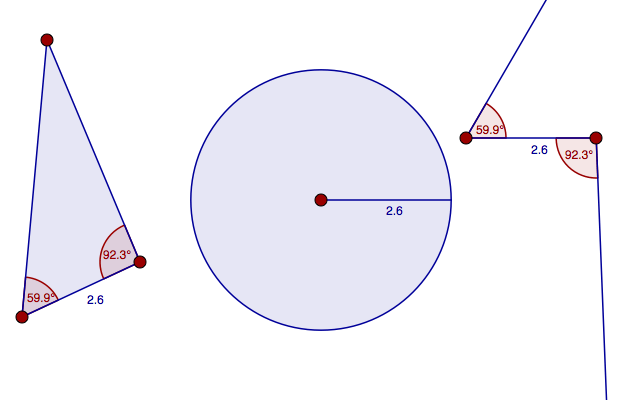
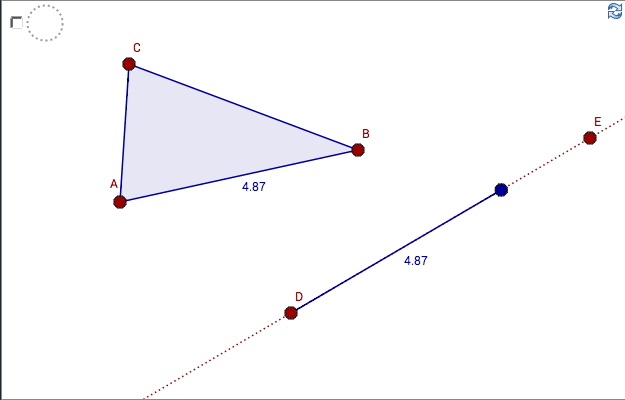
Kongruenta trianglar
Några verktyg
För att kunna undersöka olika triangelfall, behövs det verktyg för att kopiera längder och vinklar. Ett viktigt hjälpmedel är att använda cirklar för att kopiera längder. Se till att du vet hur man gör dessa uppgifter innan du fortsätter med triangelfallen.
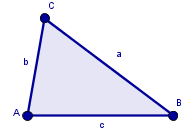
Gör en triangel i GeoGebra. Om du inte har några andra objekt kommer triangelns hörn att ligga i punkterna A, B, C. Triangelns sidor kommer att ha beteckningarna AB=c, BC=a och AC=b
Kopiera längd
Utgå från: En triangel ΔABC
Konstruera: En cirkel vars radie har längden c (c=AB). Man skall kunna flytta cirkeln.
Konstruera: En sträcka vars längd är c. Man skall kunna flytta sträckan.
Bokstäverna a, b och c är namn på triangelns sidor. De fungerar även som så kallade variabler, dvs de har numeriska värden som kan användas i matematiska uttryck. De numeriska värdena är respektive sidas längd.
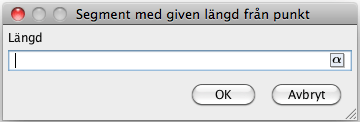
Använd verktyget
Segment med given längd från punkt. Det kommer då upp en ruta
i vilken man kan fylla i ett tal.
Prova att göra några sträckor med valfria längder. Prova att skriva c i rutan. ändra sedan på den ursprungliga triangeln.
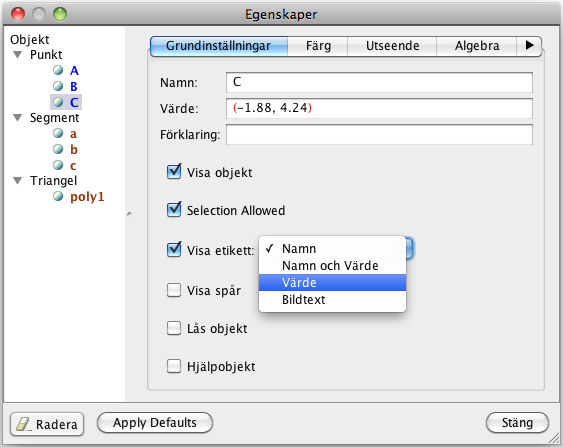
Högerklicka på ett objekt och välj Egenskaper...
Ändra inställningen på etiketterna så att värdet
visas istället för namnet.
Prova på samma sätt att göra en cirkel med radien c.
Använd verktyget
Cirkel definierad via medelpunkt och radie.
Kopiera vinkel
Utgå från: En triangel ΔABC
Konstruera: En sträcka och en stråle som har en gemensam ändpunkt. Vinkeln mellan sträckan och strålen skall vara lika stor som någon valfri vinkel i triangeln. Se till att du vet hur man placerar vinkeln vid valfri ändpunkt, medurs eller moturs.
Använd verktyget
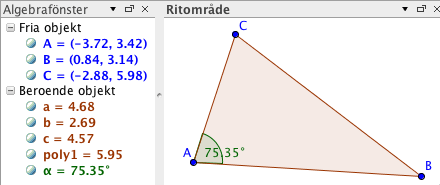
Vinkel för att mäta vinkeln BAC. Vinkeln dyker upp i algebrafönstret
med variabelnamnet α.
Lägg in en sträcka
DE. Använd verktyget
Vinkel med given storlek på sträckan DE;
skriv in α i rutan som dyker upp.
Verktyget
Vinkel med given storlek kan användas på två olika
sätt.
Om man först klickar på en sträcka och sedan fyller i en vinkel kommer vinkeln automatiskt att hamna vid sträckans första punkt.
Om man först klickar på punkten D, sedan på punkten E och sedan fyller i en vinkel, kommer vinkeln DED' att skapas, dvs vinkeln hamnar vid punkten E.
Kopiera längd till en sträcka på en given linje
Utgå från: En triangel ΔABC och en linje l genom två punkter D och E
Konstruera: En sträcka vars ena ändpunkt ligger i punkten D. Sträckan skall ha samma längd som sidan AB och den skall ligga på linjen l.
Triangelfall
Fall 1: sida - vinkel - sida
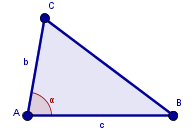
Utgå från: En triangel ΔABC med beteckningar som i figuren ovan. Sätt ut vinkeln BAC och kalla den α.
Konstruera: En ny triangel sådan att en av sidorna har längden c och en annan sida har längden b. Vinkeln mellan dessa två sidor skall vara α.
När konstruktionen är klar skall man kunna dra i alla hörnpunkter på den ursprungliga triangeln. Den andra triangeln skall kunna flyttas och roteras kring någon hörnpunkt.
sida - vinkel - sida: Slutsats -- Ändra den ursprungliga triangeln. Vilken slutsats kan man dra om kopian?
Fall 2: sida - sida - sida

Utgå från: En triangel ΔABC med beteckningar som i figuren ovan.
Konstruera: En ny triangel med samma sidlängder som den ursprungliga triangeln.
sida - sida - sida: Slutsats -- Ändra den ursprungliga triangeln. Vilken slutsats kan man dra om kopian?
Fall 3: vinkel - sida - vinkel
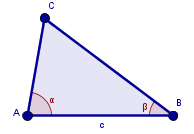
Utgå från: En triangel ΔABC med beteckningar som i figuren ovan.
Konstruera: En ny triangel där två av vinklarna har samma storlek som α respektive β och där sidan mellan dessa två vinklar har längden c.
vinkel - sida - vinkel: Slutsats -- Ändra den ursprungliga triangeln. Vilken slutsats kan man dra om kopian?
Fall 4: sida - sida - vinkel
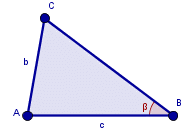
Utgå från: En triangel ΔABC med beteckningar som i figuren ovan. Sätt ut vinkeln ABC och kalla den β.
Konstruera: En ny triangel sådan att en sida har längden b, en annan sida har längden c och sådan att en vinkel som inte ligger mellan dessa två sidor har samma storlek som motsvarande vinkel i den ursprungliga triangeln.
sida - sida - vinkel: Slutsats -- Ändra den ursprungliga triangeln. Vilken slutsats kan man dra om kopian?
Fyrhörning
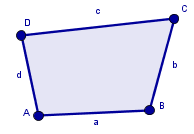
Utgå från: En fyrhörning med sidlängderna a, b, c och d
Konstruera: En ny fyrhörning med samma sidlängder.
fyrhörning: Slutsats -- Kan man dra samma slutsats som man kunde när det gällde trianglar?
Sammanfattning
Euklides Elementa
Den första boken i Euklides Elementa innehåller ett antal definitioner och postulat. Ett annat ord för postulat är axiom. Axiom är något man utgår från, något som antas vara uppenbart sant utan bevis.
Ordalydelsen i det första postulatet är: Att dra en rät linje från en punkt till en annan punkt
Detta skall utläsas: Det går att dra en rät linje från en punkt till en annan punkt
Postulaten gör det möjligt att göra så kallade passare-och-linjal konstruktioner, se Geometri - Passare och linjal. När man väl gjort en passare-och-linjal konstruktion, kan man sedan anta att det är möjligt att dela en sträcka i två lika stora delar, att dra en vinkelrät höjd i en triangel, att dela en vinkel i två lika stora vinklar, m.m.
Efter definitionerna, postulaten och passare-och-linjal konstruktionerna, följer ett antal satser vilka bevisas. När en sats väl har bevisats, får man anta att satsen är sann.
Det som följer nedan är en förenklad version:
Definitioner och axiom
Definition 1 Två linjer i ett plan som inte skär varandra är parallella.
Definition 2 Två trianglar är kongruenta om motsvarande sidor och motsvarande vinklar är lika stora. Att två trianglar ΔABC och ΔDEF är kongruenta skrivs så här ΔABC≅ΔDEF
Axiom 1 Genom två olika punkter kan man dra en och endast en linje
Axiom 2 Parallellaxiomet Genom en punkt utanför en linje kan man dra en och endast linje som är parallell med den första linjen.
Axiom 3 Flyttningsaxiomet En geometrisk figur kan flyttas, roteras och vändas utan att dess form eller storlek förändras. (Detta axiom finns inte med i Euklides Elementa men det används vid några tillfällen ändå. En utförlig diskussion finns här)
Satser
De tre första fallen du gjort som GeoGebra-övningar kallas kongruensfall 1, 2 respektive 3.
Sats 1 Första kongruensfallet "sida-vinkel-sida eller SVS"
Sats 2 Satsen om likbent triangel Om två sidor i en triangel är lika stora, så är de motstående vinklarna lika stora.
Sats 3 Andra kongruensfallet "sida-sida-sida eller SSS"
Sats 4 Tredje kongruensfallet "vinkel-sida-vinkel eller VSV"
Kommentar
Vissa läroböcker kallar kongruensfallen SAS, SSS, och ASA för postulat (eller axiom) istället för satser. I Elementa bevisas de som satser med hjälp av superposition av trianglar, en metod som senare blivit kritiserad. När Hilbert i boken The foundations of geometry (pdf) formaliserade Euclides Elementa, gjorde han en del av SAS-fallet till ett axiom.
Övning
Använd Sats 1 för att bevisa Sats 2!
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License