Complex Numbers

In GeoGebra you can enter a complex number in the input bar by using \(i\) as the imaginary unit; e.g. w=2+3i. The number appears in the graphics view as a point and you can move it around. You can also use the tool Complex Number.

There are some GeoGebra functions that work on both points and complex numbers. The functions abs(w), arg(w) and conjugate(w) are self-explanatory. In order to get the real or imaginary part, use x(w) or y(w) respectively.

It is possible to perform arithmetic operations on complex numbers, and to use some complex functions.

Complex functions

For a function \(\mathbb{C} \rightarrow \mathbb{C}\) you cannot draw a graph. Instead you can visualize how one set of points is mapped onto another set of points.

We will use following methods in GeoGebra to visualize complex functions.

Method 1 can be used to study how points are mapped onto points.

If you want to study how a set of points forming some curve is mapped, you can use the tool Locus.

If you want to map a polygon, you can place a complex point on each side of the polygon and then use Method 2 on each point. Doing this is tedious if you want to map several polygons. A more efficient approach is to use the spreadsheet.

Note that these methods do not work on functions that explicitly depend on \(\text{Re } z \), \(\text{Im } z\), \(\text{arg } z\) or \(\bar{z}\). The methods also will not work for polynomial functions having complex coefficients. The methods will only work if you use functions that can also be seen as real valued functions of a real variable.

If you want to use an easy function, such as \(f(z) = az + b\) where \(a\) and \(b\) are complex coefficients, you can write the expression a*z_1+b to create the mapped point.

Möbius transformations

Load GeoGebra worksheet

A Möbius transformation is a function \(\mathbb{C} \rightarrow \mathbb{C}\) defined by

where \(a, b, c\) and \(d\) are complex numbers such that \(ad-bc\ne 0\).

A Möbius transformation is not defined when \(z = -d/c\) since this would mean division by zero. If we instead use the so called extended complex plane, this plane also contains a point at infinity. The extended complex plane is represented by points on the so-called Riemann sphere, where the point at infinity is the top most point of the sphere.

By using the Riemann sphere, which we can write as \(\mathbb{C} \cup \{\infty \} \), we can define a Möbius transformation \(\mathbb{C} \cup \{\infty \} \rightarrow \mathbb{C} \cup \{\infty \} \) in following way:

We assume that \(ad-bc\ne 0\).

If \(c \ne 0 \) we define the function as

If \(c = 0\) we define the function as

Note that if \(c \ne 0\) we can't have that \(d = 0\) since \(ad-bc\ne 0\).

It is easy to show following properties of a Möbius transformation:

1. If \(f\) and \(g\) are Möbius transformations, then \(f \circ g\) is also a Möbius transformation. In other words, \(f(g(z)\) is a Möbius transformation.
2. A Möbius transformation \(f\) always has an inverse \(f^{-1}\). In other words, there is a function \(f^{-1}\) such that \(f(f^{-1}(z)) = f^{-1}(f(z)) = z\).

That the composition of two Möbius transformations is another Möbius transformation, means that repeated transformations can be described as composite functions.

Exercises

Most exercises assume that you know about circle inversion: Non-Euclidean Geometry ‐ Inversion in Circle.

Exercise 1

Sets in the complex plane

Describe following sets using paper and pen.

• \(1 < \text{Re } z < 5\)
• \(0 < \arg z < \pi/4\)
• \(|z-(2+i)| < 3\)

Exercise 2

Find the set

Let \(z\) and \(w\) be complex numbers such that

• Use Method 1 to make a GeoGebra construction of the mapping.

• The set \(\text{Re } z > 0 \) is mapped onto a set that can be defined by an equation in \(w\). Use your GeoGebra construction to find this set and make a conjecture. Hint: put traces on the points!

• Prove your conjecture.

• Find the inverse function \(f^{-1}\) of \(f(z) = (z-1)/(z+1)\).

Exercise 3

Comparison with circle inversion

• Make a complex point \(z_1\) in GeoGebra. Create the point \(1/z_1\).

  Make a unit circle and reflect \(z_1\) in the unit circle using the tool Reflect about Circle.

  Compare the two operations \(1/z\) and inversion of \(z\) in the unit circle. Describe how the two operations are related.

• Find the complex function corresponding to inversion in the unit circle. How does this function differ from the function \(f\)?

• Rotations, reflections and translations are transformations that preserve angles. We have also previously shown that inversion in a circle preserves angles. Does the function \(f(z) = 1/z\) preserve angles or not? Explain your thinking.

Exercise 4

Complex arithmetic's and transformations

A Möbius transformation is a composition of four functions

• \( f_1(z) = z + d/c \)
• \( f_2(z) = 1/z \)
• \( f_3(z) = \frac{bc-ad}{c^2} z \)
• \( f_4(z) = z + a/c \)

such that

• Make two complex points \(z_1\) and \(a\). Create two points \(z_1+a\) and \(z_1\cdot a\). Drag the point \(a\), for instance along the \(x\)- and \(y\)-axis.

  Describe addition and multiplication of complex numbers as transformations. Explain why your descriptions hold. In your explanation you should use the fact that a complex number can be written both as an expression \(a+bi\) and in polar form \(re^{i\theta}\).

• You can assume that inversion in a circle preserves angles. Use the four functions \(f_1, f_2, f_3, f_4\) to argue that a Möbius transformation preserves angles.

Exercise 5

Mapping of a circle

Use Method 2 to visualize how a circle is mapped by the function

and how it is mapped by the function

When your construction is done, you can change the circle by dragging the points defining it. Let the two curves have different colors so you easily can see what curve belongs to what function.

• For the function \(f\) you should be able to guess what sort of curve the circle is mapped onto. Explain your thinking about this curve.

• Are there any easy special cases of circles, cases for which you can explain the mapping of the function \(g\)?

Exercise 6

Mapping of a line

Use Method 2 to visualize how a line is mapped by the function

and how it is mapped by the function

• For the function \(f\) you should be able to guess what sort of curve the line is mapped onto. Explain your thinking about this curve.

• Are there any easy special cases of lines, cases for which you can explain the mapping of the function \(g\)?

Exercise 7

Mapping of square and a triangle

• Use Method 3 to show how a square and an equilateral triangle are mapped by the function

  \[f(z) = \frac{1}{z}.\]

• Show how the polygons are mapped by the function

  \[g(z) = az\]

  and

  \[h(z) = z + a\]

  where \(a\) is a complex coefficient. Make a complex point representing \(a\).

  Use columns D and E to show the mappings of the polygons by \(g\). Use columns F and G to show the mappings of the polygons by \(h\). You cannot use GeoGebra-functions for this but you can write the expressions of the functions directly.

• Describe and explain the transformations by \(f, g\) and \(h\).

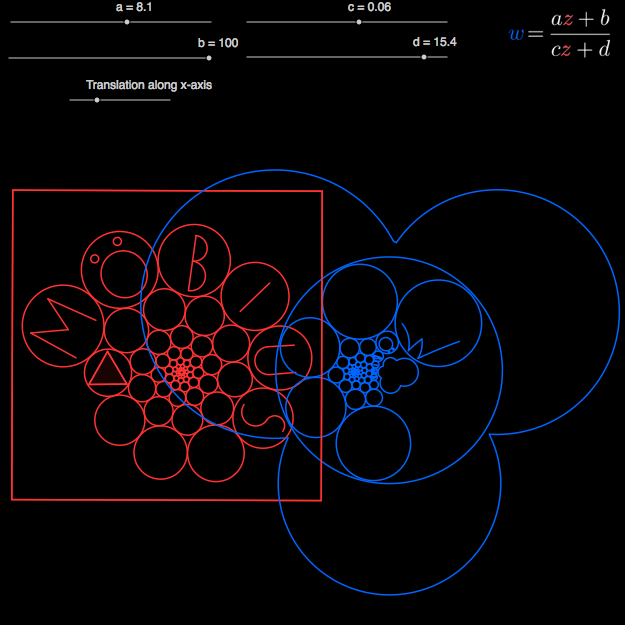
Exercise 8

Möbius transformation of a polygon

For simplicity we will only use real valued coefficients \(a, b, c, d\). Make a slider for each coefficient and write a function \(f(x)\) for the Möbius transformation defined by the sliders.

Make a GeoGebra construction visualizing how a regular polygon is transformed by the function.

• What sort of transformations do you get when \(c = 0\)?

• What sort of transformations can't you show since the coefficients are real?