Parabeln
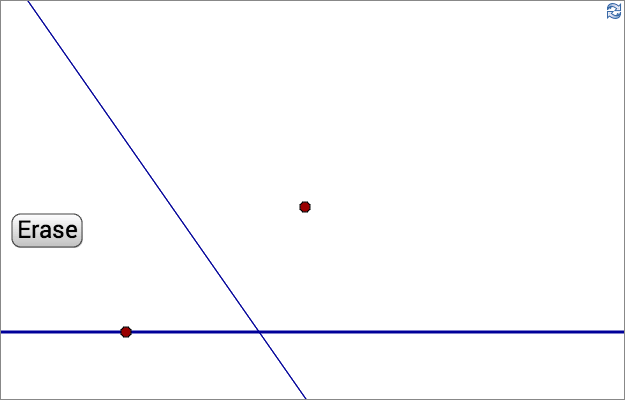
De blå linjerna är mittpunktsnormaler till de två punkterna.
Man kan åstadkomma samma sak, fast lite mer effektfullt, med hjälp av kalkylblad, se Lär dig GeoGebra - Kalkylblad.
Parabeln är ett kägelsnitt, dessa beskrivs av Apollonius i boken"Conics".
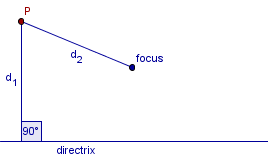
En antik definition av parabeln är:
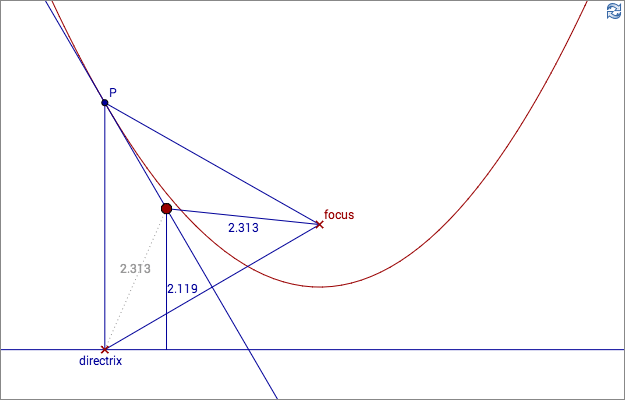
Givet en linje (en direktris) och en punkt (brännpunkten) bestäm en punkt P med avstånden (som i bilden) d1=d2. Parabeln är mängden av alla sådana punkter.
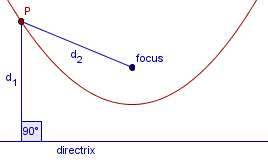
Punkten P ligger på mittpunktsnormalen. Mittpunktsnormalen skär parabeln i en enda punkt, punkten P. Den är därför en tangentlinje till parabeln.
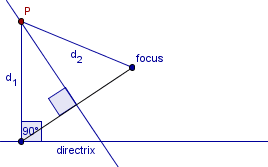
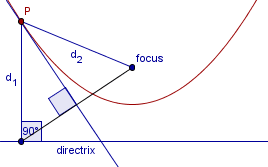
Inga andra punkter på mittpunktsnormalen ligger på parabeln.
Övning
Placera brännpunkten på y-axeln vid (0,a), direktrisen på x-axeln, och låt punkten P ha koordinaterna (x,y). Bestäm y uttryckt i x genom att använda avstånden d1=d2.
(Apollonius kunde inte göra denna övning, han skrev sin bok ungefär 1800 år innan Cartesius hittade på koordinatplanet.)
Parabelns brännpunkt
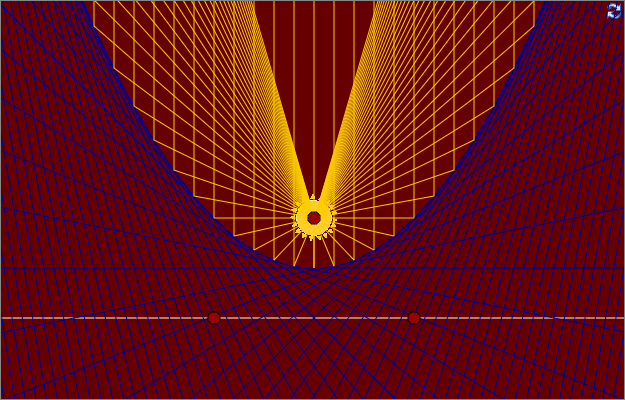
En stråle som faller in mot en spegel kommer att reflekteras så att :
infallsvinkeln = reflektionsvinkeln
Övning
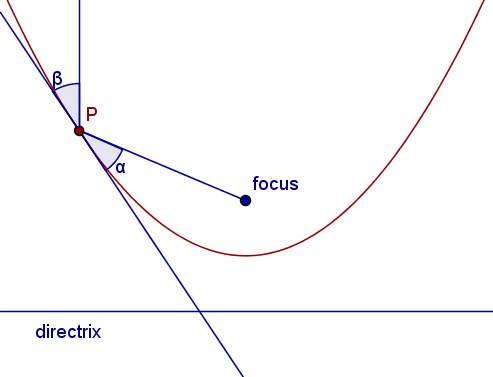
Visa att en stråle som faller in vinkelrätt mot direktrisen på en parabel kommer att reflekteras genom brännpunkten. Med andra ord, visa att α=β.
Andra kägelsnitt
Om man låter direktrisen vara en cirkel istället för en linje kan man få fram formen av andra kägelsnitt. Gör en mittpunktsnormal mellan brännpunkten och en punkt på cirkeln.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License