Inversa och sammansatta funktioner
Inversa funktioner
Låt
\[f(x)=3+2x\]vara en linjär funktion. Varje \(x\)-värde avbildas entydigt på ett \(y\)-värde som ges av \(y=3+2x\).
Eftersom funktionen är linjär, kan man också till varje \(y\)-värde, på ett entydigt sätt bestämma ett \(x\)-värde. Man kan beskriva \(x\) som en funktion av \(y\) med formeln \(x=\frac{y-3}{2}\). Denna "omvända" funktion kallas för den inversa funktionen till \(f\) och betecknas \(f^{-1}\).
Enligt konvention, brukar man låta \(y\) beteckna funktionsvärden och \(x\) de värden som en funktion verkar på. Då man bestämt den inversa funktionen (genom att lösa ut \(x\)) låter man därför \(y\) och \(x\) byta plats. Man skriver alltså \(y=\frac{x-3}{2}\).
Nu är alltså
\[f^{-1}(x) = \frac{x-3}{2}.\]Metod för att bestämma den inversa funktionen till \(f(x)\)
- Skriv som en ekvation \(y=f(x)\)
- Lös ut \(x\) som ett uttryck av \(y\).
- Byt plats på \(x\) och \(y\).
Om man betraktar grafen till en funktion, så får man grafen till den inversa funktionen genom att låta \(x\)-axeln och \(y\)-axeln byta plats.
Grafen till en invers funktion \(f^{-1}(x)\), är grafen till funktionen \(f(x)\) speglad i linjen \(y=x\).
Alla funktioner har inte en invers funktion. För vissa funktioner får man då man byter plats på axlarna, en kurva som inte kan vara grafen till en funktion.
Funktionen
\[f(x)=x^2,\]har två \(x\)-värden som hör till varje positivt \(y\)-värde. Byter man plats på \(x\)- och \(y\)-axel, får man en kurva som har två \(y\)-värden hörande till varje positivt \(x\)-värde. Denna kurva kan inte vara grafen till en funktion.
Även om funktionen \(f(x)\) inte har en invers, så finns det en snarlik funktion som har en invers. Funktionen
\[g(x) = x^2, x\ge 0\]har en invers, likaså funktionen
\[h(x)= x^2, x \le 0. \]Värdemängd och definitionsmängd
När vi talar om funktioner som bara är definierade för vissa \(x\)-värden, kan det förenkla språkbruket om vi använder rätt terminologi.
Definitionsmängden till en funktion \(f(x)\)
är mängden av alla \(x\)-värden
för vilken funktionen är definierad.
Värdemängden till en funktion \(y=f(x)\)
är mängden av alla \(y\)-värden
som funktionen antar.
Om man låter \(V_f\) beteckna värdemängden och \(D_f\) definitionsmängden till en funktion \(f(x)\), gäller det att:
\[V_f=\left\{f(x)| x\in D_f\right\}\]
För funktionen
\[f(x)=3+2\sin(x)\]är \(D_f = \mathbb{R}\) och \(V_f= [1, 5]\). Istället för att skriva värdemängden som ett intervall, kan vi skriva det som en olikhet, som \(V_f: 1\le y \le 5\) eller mer formellt med mängdnotation som \(V_f = \{ y| 1\le y \le 5 \} \).
Begränsa definitionsmängden
Som vi tidigare nämnt, måste man ibland begränsa värdemängden för att en funktion ska kunna ha en invers. För funktionen
\[f(x) = x^2\]kan vi antingen begränsa värdemängden till \(D_f: x\ge 0 \), då får vi att \(f^{-1}(x)= \sqrt{x}\), eller så kan vi begränsa värdemängden till \(D_f: x\le 0 \) och får då att \(f^{-1}(x)= -\sqrt{x}\).
Eftersom \(x\) och \(y\) byter plats när vi bestämmer en invers funktion, måste det gälla att: definitionsmängden till en funktion, blir värdemängden till den inversa funktionen; värdemängden blir definitionsmängd.
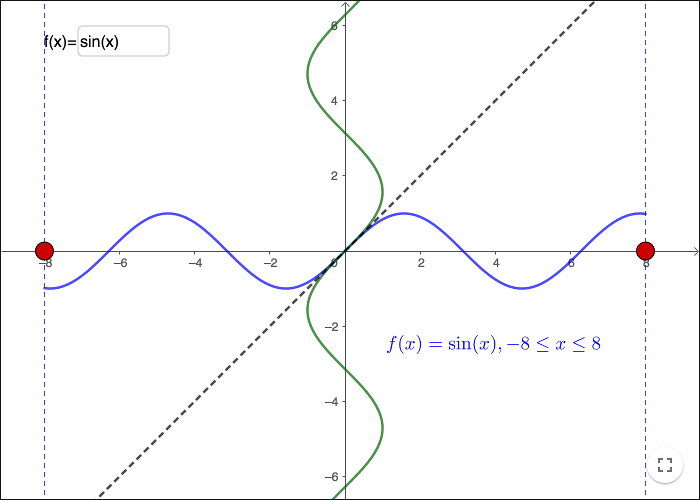
För periodiska funktioner, finns det oändligt många olika sätt att begränsa värdemängden.
I arbetsbladet ovan kan du se att det finns flera sätt att begränsa definitionsmängden till \(\sin(x)\) så att det går att definiera en invers. Exempelvis kan du begränsa \(x\) till \(\frac{\pi}{2}\le x \le \frac{3\pi}{2} \), i sådant fall får inversen värdemängden \(\frac{\pi}{2}\le y \le \frac{3\pi}{2} \) och definitionsmängden \(-1\le x \le 1\).
Enligt konventionen definieras värdemängd och definitionsmängd till inversa trigonometriska funktioner så här:
| funktion | definitionsmängd | värdemängd |
|---|---|---|
| \(\arcsin x\) | \(-1\le x \le 1\) | \(-\frac{\pi}{2}\le y \le \frac{\pi}{2}\) |
| \(\arccos x\) | \(-1\le x \le 1\) | \(0\le y \le \pi\) |
| \(\arctan x\) | \(x \in \mathbb{R}\) | \(-\frac{\pi}{2}\lt y \lt \frac{\pi}{2}\) |
De inversa trigonometriska funktionerna skrivs asin, acos och atan i GeoGebra och de flesta programmeringsspråk.
Sammansatta funktioner
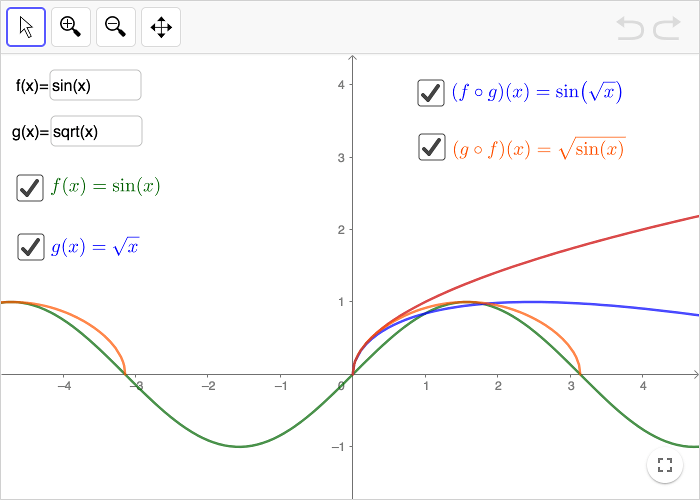
En sammansatt funktion är en funktion av en funktion. Man använder symbolen \(\circ\) för att beteckna en sammansatt funktion.
\[(f\circ g)(x)=f(g(x))\]
I GeoGebra är det enkelt att göra sammansatta funktioner. Om du har definierat två funktioner \(f(x)\) och \(g(x)\), kan du skriva
f(g(x))
för att skapa den sammansatta funktionen \(h(x) = (f \circ g)(x)\). Du skriver
g(f(x))
för att skapa den sammansatta funktionen \(p(x) = (g \circ f)(x)\).
Värdemängd och definitionsmängd för sammansatta funktioner
Betrakta funktionen
\[f(x) = 2^{\sqrt{4\sin x}},\]vilken kan ses som en sammansättning av flera funktioner. För att bestämma värdemängd och definitionsmängd kan vi börja med att studera grafen.
Värdemängden ser ut att vara \([1,4]\). Det är tydligt att definitionsmängden inte är \(\mathbb{R}\).
Av funktionerna \(g(x) = 2^x \), \(h(x) = \sqrt x\) och \(p(x) = 4\sin x\), är det bara \(h\) som har en definitionsmängd som inte är \(\mathbb{R}\). För den sammansatta funktionen \( f = g \circ h \circ p\), är värdemängden till \(p\) definitionsmängden till \(h\).
Värdemängden till \( p(x) = 4\sin(x)\) är intervallet \([-4,4]\) men eftersom vi inte kan tillåta negativa funktionsvärden, måste definitionsmängden begränsas. Eftersom \(p\) är den innersta funktionen, är definitionsmängden till \(p\) också definitionsmängden till \(f\).
\[D_f = \{x | 2n\pi \le x \le (2n+1)\pi, n \in \mathbb{Z} \}\]Värdemängden till \(p(x) = 4 \sin(x) \) är nu \([0,4]\). Detta är definitionsmängden till \(h(x) = \sqrt{x}\).
Eftersom \(h(x) = \sqrt{x}\) har definitionsmängden \([0,4]\), blir dess värdemängd \([0, 2 ]\). Detta är definitionsmängden till \(g(x) = 2^x \).
Eftersom \(g(x) = 2^x \) har definitionsmängden \([0, 2 ] \), blir dess värdemängd \([1, 4] \). Detta är definitionsmängden till funktionen \(f\).
\[R_f: [1, 4]\]Sammansättning av en funktion och dess invers
Om definitionsmängden och värdemängden till en funktion \(f(x)\) bägge är \(\mathbb{R}\), och om \(f(x)\) har en invers \(f^{-1}(x)\), så är:
\((f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x\).
Betrakta exempelvis
\[f(x)=3+2x \Longleftrightarrow f^{-1}(x)=\frac{x-3}{2}\].Vi har att
\[(f\circ f^{-1})(x)=f(f^{-1}(x))=f(\frac{x-3}{2})=3+2\frac{x-3}{2}=x\]
och
\[(f^{-1}\circ f)(x)=f^{-1}(f(x))=f^{-1}(3+2x)=\frac{3+2x-3}{2}=x\]

Om definitionsmängden eller värdemängden till \(f(x)\) är begränsad, så blir sammansättningarna av en funktion och dess invers också \(x\), men endast på ett intervall.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License