Kvadratiska funktioner
Det vanligaste sättet att skriva en kvadratisk funktion är att använda allmän form:
\[f(x)=ax^2+bx+c\]
Om man vill analysera grafen till en kvadratisk funktion, eller studera sambandet mellan grafen och lösningar till andragradsekvationer, är två andra former lämpligare: vertexform och faktorform.
För att kunna skriva om en kvadratisk funktion från allmän form till vertexform, måste du kunna kvadratkomplettera.
Kvadratkomplettering
Kvadratkomplettering är en metod för att lösa andragradsekvationer och att skriva om kvadratiska funktioner till vertexform.
Det är enkelt att lösa ekvationer på formen \(x^2= c\), man tar roten ur i båda leden. Det är även enkelt att lösa ekvationer på formen \(ax^2+b=c\), man börjar med at ta roten ur, sedan löser man ut \(x\). Med kvadratkomplettering skriver man om en ekvation till formen \(ax^2+b=c\).
Om vi vill lösa en ekvation på formen
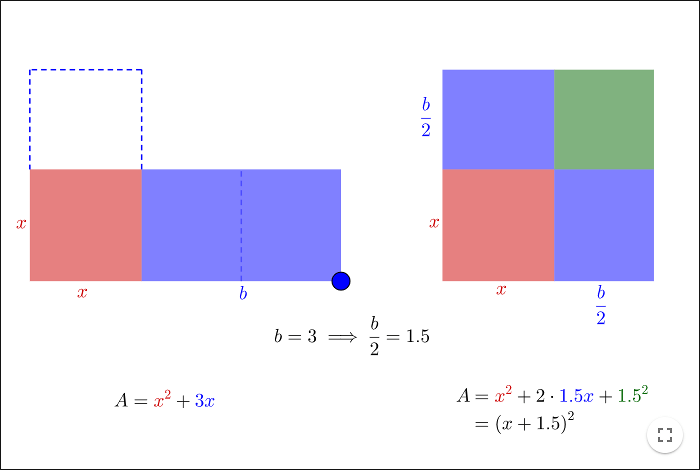
\[x^2+bx=a\]där både \(b\) och \(a\) är positiva tal, då kan vi använda areor för att beskriva kvadratkomplettering.
Från arbetsbladet får vi att
\[ \begin{align} x^2+bx &= a \\ x^2+bx + \left(\frac{b}{2}\right)^2 &= a + \left(\frac{b}{2}\right)^2 \\ \left(x+\frac{b}{2}\right)^2 &= a + \left(\frac{b}{2}\right)^2 \end{align} \]vilket är en ekvation vi kan lösa.
Man kan göra en liknande geometrisk konstruktion för att lösa ekvationen då \(b\) är negativt, men så länge man håller på med geometriska tolkningar så kan \(a\) inte vara negativt och man får inte fram några negativa värden på \(x\). För att kunna hantera alla fall och få med alla lösningar bör en algebraisk metod användas.
Den första att hitta en metod för att lösa andragradsekvationer var Brahmagupta som också gjorde ett av de största bidragen till mänskligheten genom historien ‐ han visade hur man kunde göra beräkningar med talet noll.
Vertex form
En andragradsfunktion kan alltid skrivas på formen
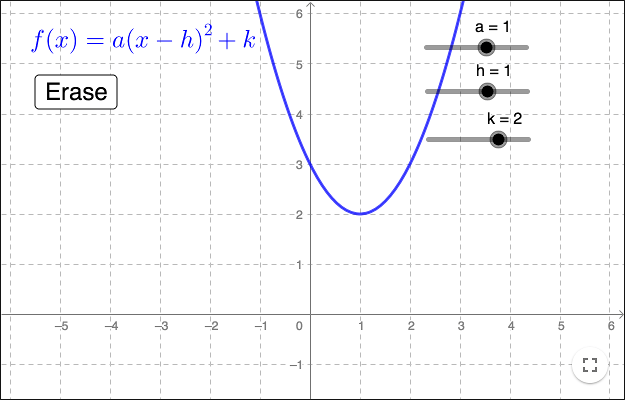
\[ f(x) = a(x-h)^2+k\]vilket kallas vertexform.
Vilken punkt ligger alltid på grafen oavsett vilket värde \(a\) har?
Translationer av grafer
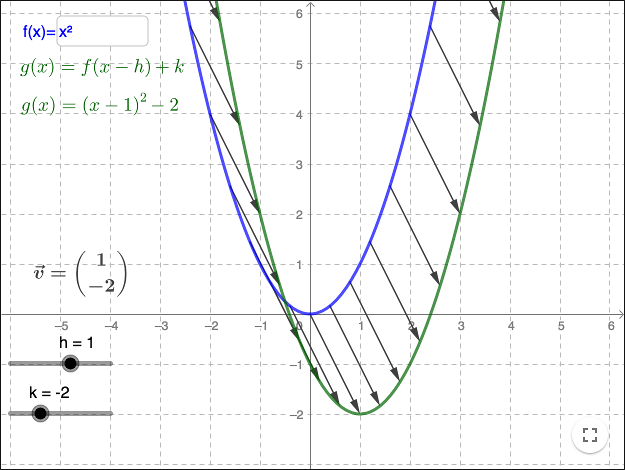
Grafen till en andragradsfunktion \(g\) på formen \(g(x)=(x-h)^2+k\), kan ses som en translation av grafen till \(f(x)=x^2\) längs vektorn
\[ \binom{h}{k}. \]Från allmän form till vertexform
För att skriva om en andragradsfunktion på allmän form till vertexform, kan man kvadratkomplettera, vilket i det allmänna faller ger att
\[ \begin{align} f(x) &= ax^2+bx+c \\ &= a\left( x^2+\frac{b}{a}x+\frac{c}{a}\right) \\ &= a\left( x^2+2\frac{b}{2a}x+ \left(\frac{b}{2a} \right)^2-\left(\frac{b}{2a} \right)^2+\frac{c}{a}\right) \\ &= a\left( \left(x + \frac{b}{2a}\right)^2 -\left(\frac{b}{2a} \right)^2+\frac{c}{a}\right) \\ &= a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a} \end{align} \]Faktorform
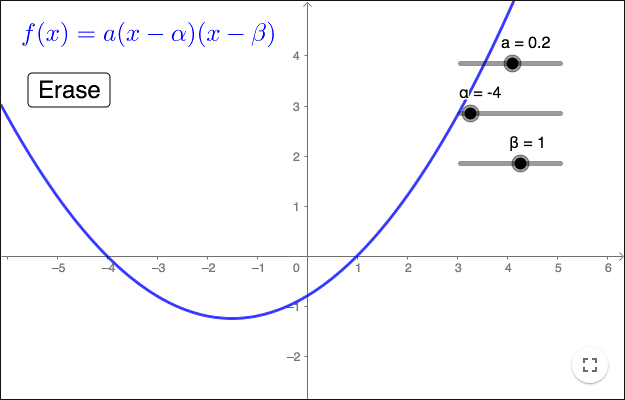
En andragradsfunktion kan alltid skrivas på formen
\[ f(x) = a(x-\alpha)(x-\beta\]vilket kallas vertexform. Koefficienterna \(\alpha\) och \(\beta\) är rötterna till andragradsekvationen \(f(x) = 0\).
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License