Linjära funktioner
Lutning


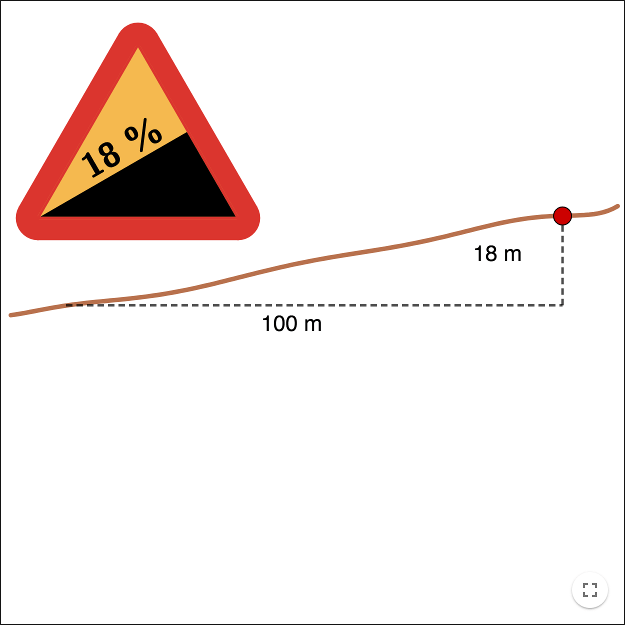
Den tioprocentiga lutningen i vägskyltarna ovan betyder att om man förflyttas 100 m i horisontell led, så förflyttas man i genomsnitt 10 m i vertikal led.
För att få fram procenttalet, tar man förflyttningen i \(y\)-led och delar med förflyttningen i \(x\)-led, \(\frac{10}{100}=0.1=10\)%.
Skyltarna förutsätter att man kör från vänster till höger, och att man på så vis kan lista ut huruvida lutningen är uppåt eller nedåt.
När man definierar lutning inom matematiken, gör man det på motsvarande vis. Man definierar lutningen som skillnaden i \(y\)-led delat med skillnaden i \(x\)-led. För att skilja på lutningar uppåt eller nedåt, säger man att skillnaden i \(y\)-led är negativ, om lutningen går "nedåt" då man går från vänster till höger.
Istället för ordet "skillnaden", använder man beteckningar med hjälp at \(\Delta \). Skillnaden i \(y\)-led betecknas \(\Delta y\) och skillnaden i \(x\)-led med \(\Delta x\). Om man låter \(k\) beteckna lutningen, får man definitionen: \[k=\frac{\Delta y}{\Delta x}\]
Om \(k\) betecknar lutningen, så ges \(k\) av
\[m=\frac{\Delta y}{\Delta x}\]Mäta lutning i GeoGebra
Om du har en linje i GeoGebra, kan du mäta linjens lutning med verktyget Lutning.
GeoGebra visar lutningen på så vis att \(\Delta x\) alltid är lika med ett.
GeoGebra-sättet att visa lutningen kan ses som en alternativ definition av lutning:
Om förändringen längs
\(x\)-axeln (då man går från vänster till höger) är 1,
så är ändringen längs \(y\)-axeln lutningen.
Räta linjens ekvation
En linje kan skrivas med en ekvation kallad k-form, vilken skrivs som
\[y = kx + m,\]där \(k\) är lutningen och \(m\) är var linjen skär \(y\)-axeln. Vertikala linjer kan inte skrivas på detta sätt eftersom lutningen inte är definierad för en vertikal linje. Istället skrivs vertikala linjer på formen
\[x = m,\]där \(m\) är någon konstant.
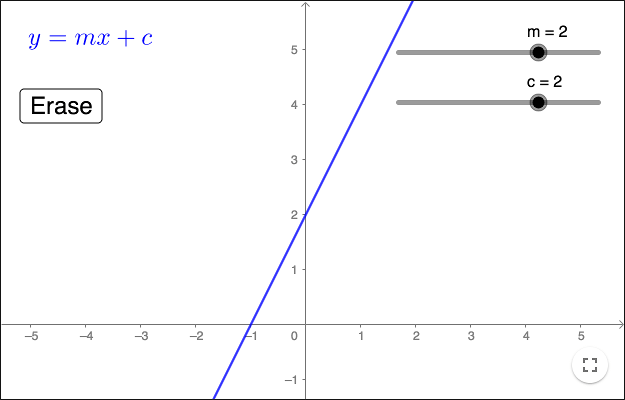
Ändra lutningen \(m\) för att se många linjer som skär \(y\)-axeln i samma punkt.
Ändra \(c\) för att se många linjer med samma lutning.
Enpunktsform
Om du vet att en punkt \((x_1, y_1)\) ligger på en linje, och om du vet att linjens lutning är \(k\), då kan du skriva linjens ekvation på formen
\[y = k(x-x_1)+y_1.\]Allmän form
När allmän form används för att skriva en linjes ekvation, skrivs ekvationen på formen
\[ax+by=c.\]Den stora skillnaden mellan allmän form och \(k\)-form, är att på allmän form finns det en koefficient \(b\) framför \(y\). När \(b=0\) är linjen vertikal.
Linjära funktioner
En linjär funktion är en funktion vars graf är en linje. En linjär funktion kan skrivas som
\[y = kx + m,\]eller som
\[f(x) = kx +m.\]Om du skriver in \(y = kx + m\) i GeoGebra, där \(k\) och \(m\) antingen representeras av glidare eller skrivs in som tal, då kommer linjen att få ett funktionsnamn \(f\).
Linjär och exponentiell tillväxt
Om du vill modellera en situation där någonting växer lika mycket för varje tidssteg, då kan du använda en linjär funktion. Det är stor skillnad på sådan så kallad linjär tillväxt och om du har någonting som växer procentuellt, i vilket fall du har exponentiell tillväxt.
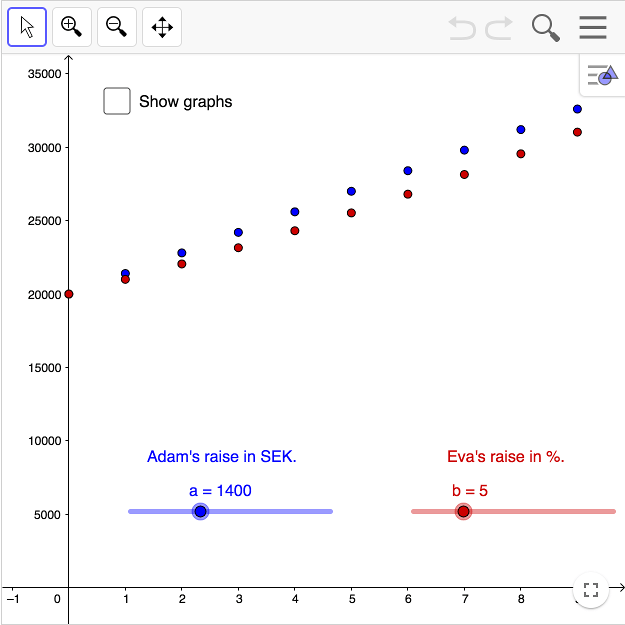
Adams löneförhöjning är linjär, Evas är exponentiell.
"Altogether, Adam lived 930 years, and then he died.."
Visa graferna. Zooma ut och kolla in Evas lön 930 år senare!
Övningar
Övning 1
Riktningskoefficienter för vinkelräta linjer
Gör en linje genom två punkter \(A\) och \(B\).
Gör en linje vinkelrät mot den första linjen genom punkten \(A\).
Använd verktyget
 Lutning på bägge linjerna.
Lutning på bägge linjerna.Döp om riktningskoefficienterna till \(k_1\) och \(k_2\).
Gör en ny variabel \(produkt\) genom att skriva in:
produkt = k_1*k_2
Rör på punkterna! Dra en slutsats om produkten! Bevisa din slutsats!
Tips: Betrakta de lutningar som visas av GeoGebra och försök använda likformiga trianglar.
Övning 2
Linjär och procentuell tillväxt
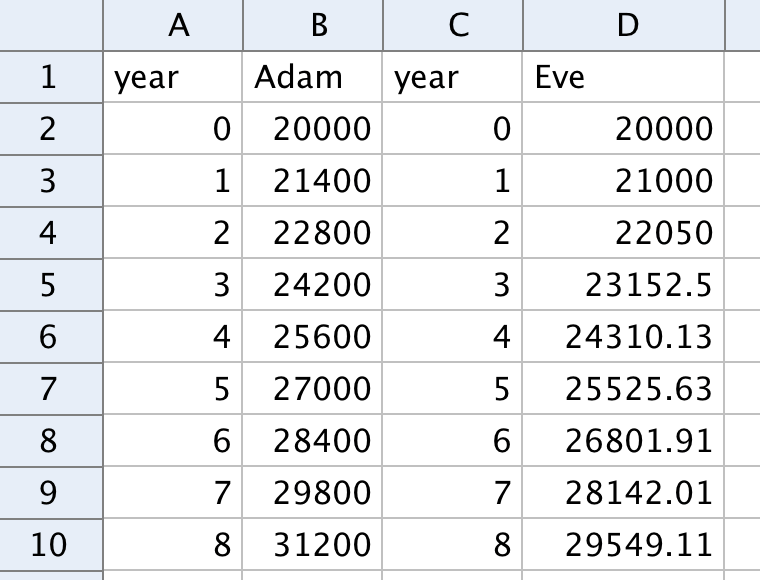
Antag att Adam och Eva bägge har 20 000 kr i månadslön. Adam förhandlar fram en löneförhöjning på 1400 kr per år i höjd månadslön. Eva förhandlar fram en löneförhöjning på 5% per år i höjd månadslön.
2.a - Visa löneförhöjningarna med fasta siffror
Lägg in en års-kolumn för Adam och en års-kolumn för Eva i kolumnerna A och C. Utnyttja relativ kopiering.
Lägg in 20000 i B2 och D2. Skriv in en kalkylblads-formel för Adams löneförhöjning med 1400 kr i B3. Gör en relativ kopiering längs kolumnen B. Lista ut vilken förändringsfaktor som skall användas för en höjning med 5% och använd denna förändringsfaktor för att skriva in en kalkylblads-formel för Evas löneförhöjning i D3. Gör en relativ kopiering längs kolumnen D. Cellerna skall åskådliggöra de två lönerna 20 år fram i tiden.
Gör två punktlistor, en för Adam och en för Eva, och se till att alla punkter syns i ritområdet.
2.b - Från fasta siffror till variabler
Lägg in 1400 i en variabel \(a\), och Evas förändringsfaktor 5 i en variabel \(e\) (dessa skrivs in i imatningsraden). Byt kalkylblads-formlerna i cellerna B3 och D3 så att dessa använder variablerna istället för fasta siffror. Gör nya relativa kopieringar längs kolumnerna B och D.
Gör två nya punktlistor. Prova att ändra värde på variablerna genom att högerklicka på dem och gå in i egenskapsfönstret. Ändra Adams löneförhöjning till 2000 kr och Evas till 8%. Då ett variabelvärde ändras, ändras alla celler som beror på denna variabel och även alla punkter.
2.c - Från variabler till glidare
Betrakta de två variablerna i algebrafönstret. Klicka i de två små cirklarna så att de blir ifyllda. Då skapas två så kallade glidare. Med en glidare kan man variera värdet på en variabel.
Öppna egenskapsfönstret för vardera glidare. Se till att Adams löneförhöjning kan varieras mellan 0 och 10000 kr, och att Evas kan variera mellan 0 och 50%.
Övning 3
Annuitetslån
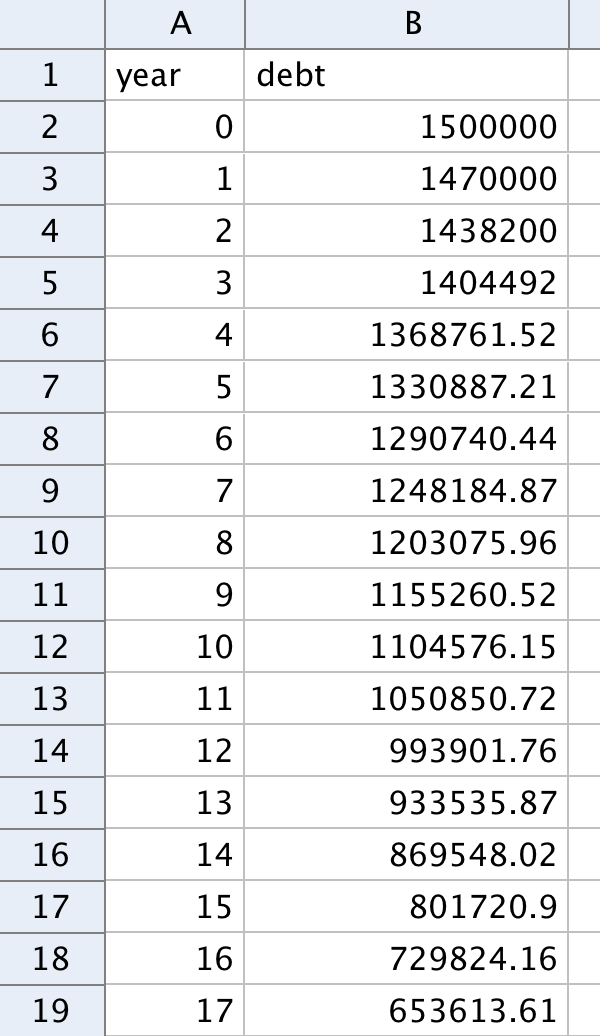
Med ett annuitetslån betalar man samma summa pengar vid varje avbetalning.
För att räkna på annuitetslån krävs det att man använder så kallade geometriska serier. Man kan dock åskådliggöra den kvarvarande skulden med hjälp av kalkylblad, utan att använda geometriska serier.
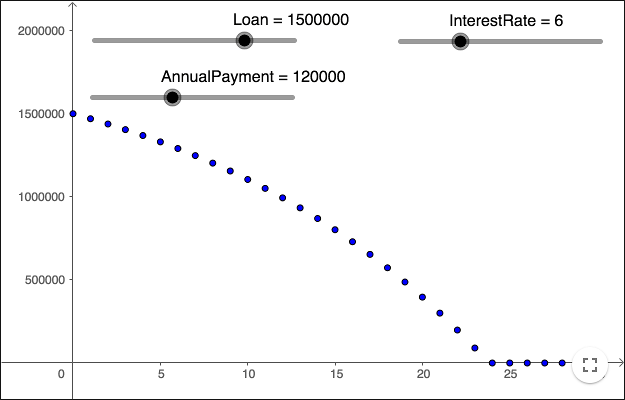
För att modellera ett annuitetslån använder man tre variabler, en för att representera hur stort lånet är, en för att representera den årliga räntan, och en för att representera den årliga avbetalningen. Gör tre variabler med valfria namn och låt lånet vara 1 500 000 kr, årsräntan 6% och den årliga avbetalningen 120 000 kr.
Låt kolumn A representera åren och kolumn B den kvarvarande skulden. Se bilden till höger.
Lägg in variabeln för lånet i cellen B2.
I cellen B3 skall det skrivas in en kalkylblads-formel för hur stor skulden är efter ett år, efter det att skulden först räknats upp med rätt förändringsfaktor och sedan minskats med en avbetalning. Gör en relativ kopiering 30 år fram i tiden.
Åskådliggör den kvarvarande skulden i ritområdet som punkter.
Gör om alla variabler till glidare.
Om du vill att resultatet ska se ut ungefär som arbetsbladet ovan, så att den kvarvarande skulden aldrig är mindre än noll, då kan du ta maximum av din formel och noll.
Max(<din formel>, 0)
Ställ in årsräntan till 8% och låt lånet vara 1 500 000 kr. Testa olika stora årliga avbetalningar.
Besvara frågan:
Hur mycket måste den årliga avbetalningen minst vara för att man säkert skall betala av hela lånet på högst 30 år om lånet är på 1 500 000 kr och om skulden ökar med en årlig ränta på 8%?
Kommentar
Man behöver inte gå omvägen att först göra en variabel som sedan görs om till en glidare, man kan
göra en glidare från början genom att använda verktyget
Glidare.
referens:
bilderna på vägskyltarna från: http://commons.wikimedia.org/wiki/Category:Slope_signs
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License