Trigonometric Functions
Transformations
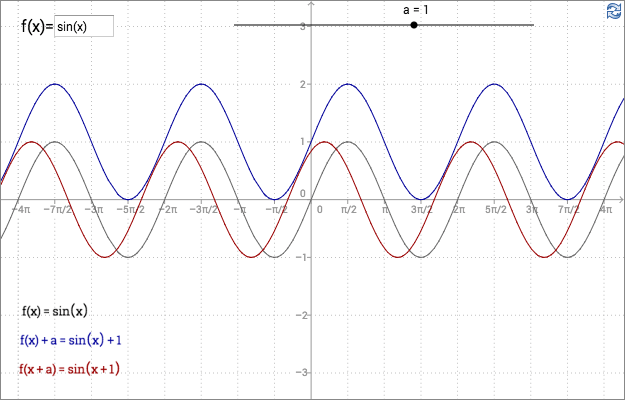
The graph of \(f(x)+ a\) is the graph of \(f(x)\)
translated \(a\) units along the \(y\)-axis .
The graph of \(f(x+ a)\) is the graph of \(f(x)\)
translated \(-a\) units along the \(x\)-axis.
To understand why it is \(-a\) units along the x-axis, consider the equality \(\sin 0=0\). The equation \(\sin (x+a)=0\) has a root when \(x+a=0 \Leftrightarrow x=-a\). The point \((0,0)\) on the graph of \(\sin x\) corresponds to the point \((-a,0)\) on the graph of \(\sin (x+a)\).
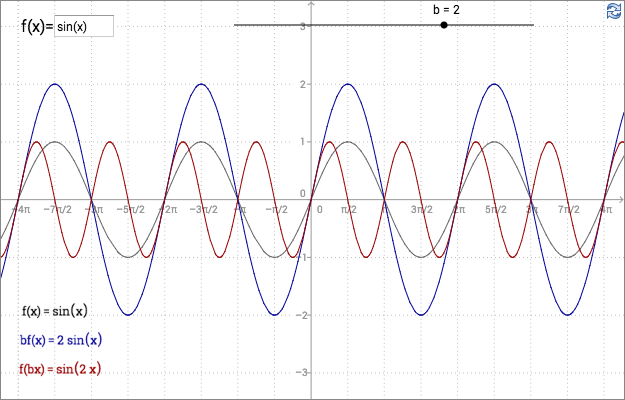
The graph of \(bf(x)\) is the graph of \(f(x)\)
stretched by a factor \(b\) along the \(y\)-axis.
The graph of \(f(bx)\) is the graph of \(f(x)\)
stretched by a factor \(1/b\) along the \(x\)-axis.
To understand why it is a factor \(1/b\) along the x-axis, consider the equality \(\sin 2\pi =0\). The equation \(\sin (bx)=0\) has a root when \(bx=2\pi \Leftrightarrow x=\frac{2\pi}{b}\). The point \((2\pi,0)\) on the graph of \(\sin x\) corresponds to the point \(( \frac{2\pi}{b} ,0)\) on the graph of \(\sin (bx)\).
If a periodic function \(f(x)\) has the period \(P\),
then the function \(f(bx)\) has the period \(\frac{P}{b}\).
Combined transformations
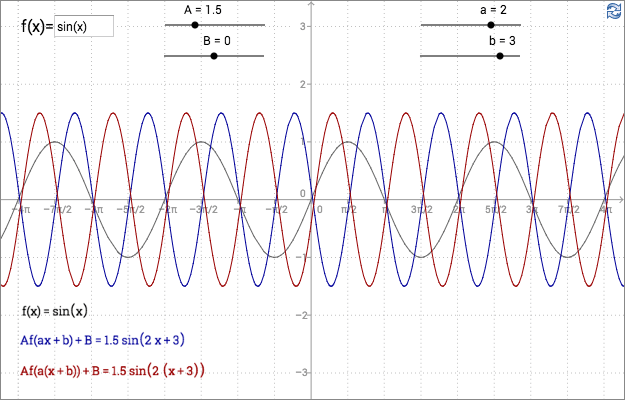
The number \(A\) in the applet above is called the amplitude of a sine or cosine function. The amplitude is half the difference between the maximum and the minimum value of a sine or a cosine function. The amplitude is never negative. Moving the functions along the y-axis by changing the slider B, does not change the amplitude.
When transforming \(\sin (x)\) to \(A\sin (ax+b)+B\), the stretch by the factor \(\frac{1}{a}\) is done before the graph is translated \(-b\) units along the x-axis. The point \((0,0)\) on the graph of \(\sin (x)\), corresponds to the point \((\frac{-b}{a},B)\) on the graph of \(A\sin (ax+b)+B\).
When transforming \(\sin (x)\) to \(A\sin (a(x+b))+B\), the graph is translated \(-b\) units along the x-axis before it is stretched by the factor \(\frac{1}{a}\). The point \((0,0)\) on the graph of \(\sin (x)\), corresponds to the point \((-b,B)\) on the graph of \(A\sin (a(x+b))+B\).
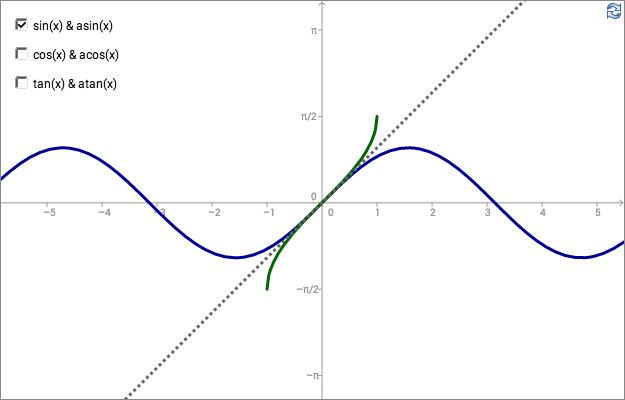
Inverse trigonometric functions
For en explanation of inverse functions, see Functions - Inverse and Composite Functions.
The inverse functions of sine, cosine and tangent are written \(\arcsin(x)\), \(\arccos(x)\)
and \(\arctan(x)\) respectively. In GeoGebra and most other computer programs they are written
asin(x), acos(x) and atan(x) respectively.
You can restrict the domain of a trigonometric function in infinitely many ways to enable a definition of an inverse function. By convention, however, the inverse functions are defined like this:
| function | domain | range |
|---|---|---|
| \(\arcsin x\) | \(-1\le x \le 1\) | \(-\frac{\pi}{2}\le y \le \frac{\pi}{2}\) |
| \(\arccos x\) | \(-1\le x \le 1\) | \(0\le y \le \pi\) |
| \(\arctan x\) | \(x \in \mathbb{R}\) | \(-\frac{\pi}{2}\lt y \lt \frac{\pi}{2}\) |
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License