The Unit Circle

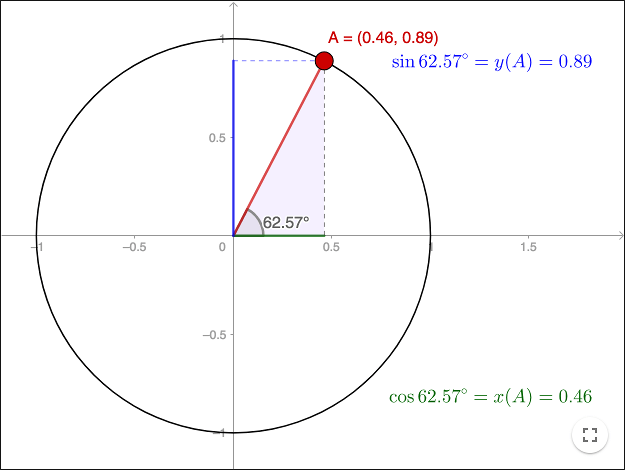
Since the trigonometric ratios do not depend on the size of the triangle, you can always use a right-angled triangle where the hypotenuse has length one. You can place such a triangle in a Cartesian system in such a way that one vertex will lie on a circle with radius one. A circle having the radius one is called a unit circle. When the hypotenuse is one, the values of sine and cosine are:

\[\sin \alpha = \frac{\text{opp}}{\text{hyp}}=\text{opp} \hspace{1cm} \cos \alpha = \frac{\text{adj}}{\text{hyp}}=\text{adj}\]

Load GeoGebra worksheet

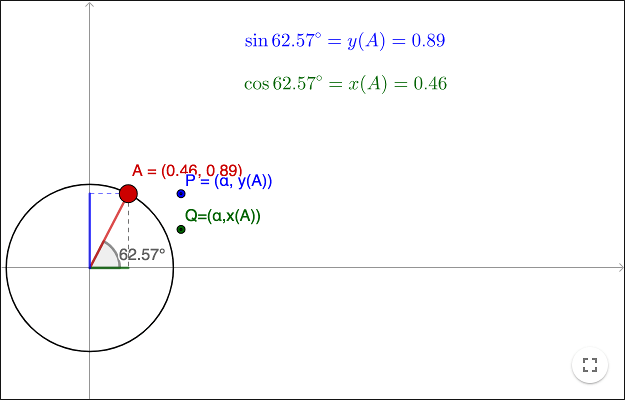
As can be seen in the worksheet, it is also true that \(\sin \alpha = y(A)\) and \(\cos \alpha = x(A)\) where \(x(A)\) and \(y(A)\) are the \(x\)- and \(y\)-coordinate respectively of \(A\). Using the coordinates of \(A\), instead of ratios of sides in a right-angled triangle, we can extend the definition of sine and cosine so they are defined for all angles.

In GeoGebra, all angles are shown as non-negative and less than \(360^\circ\). However, if an angle is extended from the positive \(x\)-axis in a clockwise order, it is a negative angle. Furthermore, angles can be larger than \(360^\circ\). Using the unit circle definition of sine and cosine, these functions are defined for all angles. Note that the triangle definition is still valid for an angle \(\alpha\) if \(0\lt \alpha \lt 90^\circ\).

The graphs of sine and cosine

Load GeoGebra worksheet

If you enter sin(x) or cos(x) in the input bar in GeoGebra, you will see the graphs of sine or cosine for all values of \(x\). The parts of the graphs that are plotted in the applet above, are repeated infinitely many times. The functions are periodic and the period is \(360^\circ\).

If \(f(x)\) is a periodic function with period \(P\), then \(f(x)=f(x+P)\) for all \(x\).

Plotting trigonometric functions using degrees in GeoGebra

You may notice that the scale on the \(x\)-axis does not correspond to the angle. The reason for this is that GeoGebra uses the unit radians instead of degrees for angles. If you want GeoGebra to use degrees, you must enter the degree-symbol, press Ctrl+O to write the degree-symbol. The code entered should be sin(x°) or cos(x°).

Rescale the \(x\)-axis by pressing Shift and then drag the \(x\)-axis. In the properties window for the graphics view, you can change the distance between labels and add the degree symbol as a unit.

Extending the definition of tangent and cotangent

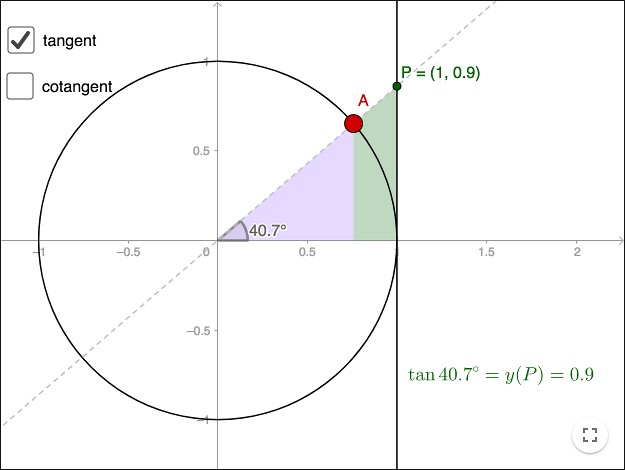
Using the triangle definition, tangent and cotangent are defined as

Load GeoGebra worksheet

Using similar triangles, you can show that the construction in the worksheet holds for angles that form a right-angled triangle. Now we can extend the definition to hold for all angles, by using coordinates of \(P\) and \(Q\) as in the worksheet.

The graphs of tangent and cotangent

Load GeoGebra worksheet

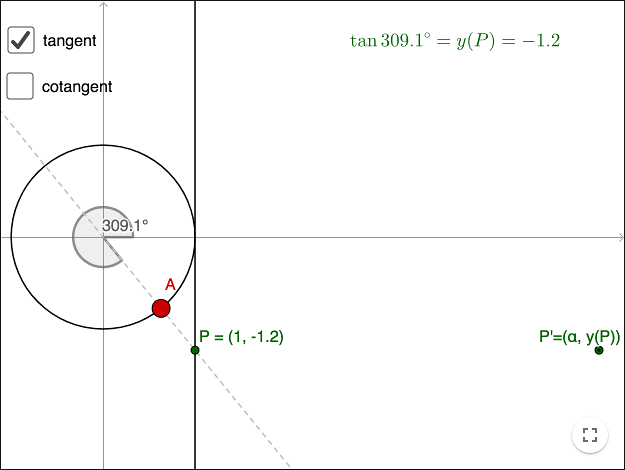
Tangent and cotangent are periodic functions with the period \(180^\circ \).

\(\tan \alpha\) is not defined when \(\alpha = 90^\circ +n\cdot 180^\circ, n \in \mathbb{Z} \).

\(\cot \alpha \) is not defined when \(\alpha = n\cdot 180^\circ, n \in \mathbb{Z} \).

Radians

Load GeoGebra worksheet

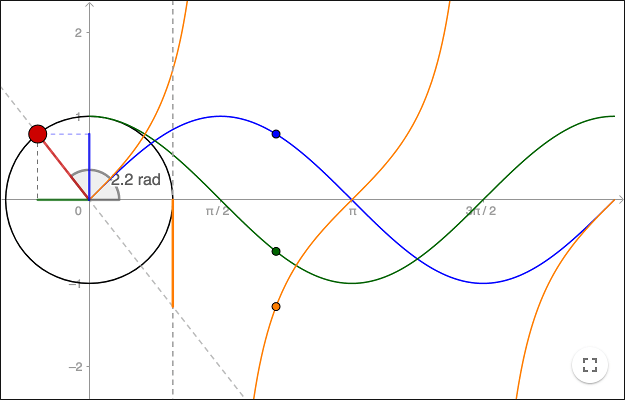
In the worksheet above, the \(x\)-coordinates of the blue, green and orange points are given by the angle. As can be seen by the labels on the \(x\)-axis, one revolution does not correspond to 360 but to \(2\pi\). In other words, one revolution corresponds to the total path travelled by the red point, which is the circumference of the unit circle.

You can change the angle unit to radians in GeoGebra under Options->Settings..., then choose the Advanced tab.

Exercises

Exercise 1

Arcs

• Make a unit circle through two points \(A=(0,0)\) and \(B=(1,0)\).
• Enter a point \(C\) on the circle and mark the angle \(\angle BAC\).
• Make sure that radians is chosen under the Advanced-tab under Options->Settings....
• Use the tool Circular Arc on the points \(A, B, C\).
• Change the radius of the circle and the angle. Observe the length of the arc.

What is the length of the arc in terms of the radius \(r\) and the angle \(\alpha\), if radians are used as angle unit?

What is the length if degrees are used as angle unit?

Exercise 2

Sectors

• Delete the arc.
• Use the tool Circular Sector on the points \(A, B, C\).
• Change the radius of the circle and the angle. Observe the area of the sector.

What is the area of the sector in terms of the radius \(r\) and the angle \(\alpha\), if radians are used as angle unit?

What is the area if degrees are used as angle unit?