Inverse and Composite Functions
Inverse functions
Let
\[f(x)=3+2x\]be a linear function. Each \(x\)-value is mapped onto a unique \(y\)-value that is given by \(y=3+2x\).
Since the function is linear, you can also find a unique \(x\)-value for each \(y\)-value. You can describe \(x\) as a function of \(y\) by letting \(x=\frac{y-3}{2}\). This "reverse" function is called the inverse function of \(f\) and it is denoted \(f^{-1}\).
By convention \(y\) is used to denote the function value and \(x\) is used for the variable. After finding the inverse function (by expressing \(x\) in terms of \(y\)), you swap the \(y\) and the \(x\), which yields \(y=\frac{x-3}{2}\).
We now have that
\[f^{-1}(x) = \frac{x-3}{2}.\]Method for finding the inverse function of \(f(x)\)
- Write it as an equation \(y=f(x)\)
- Solve for \(x\), i.e. write \(x\) as an expression of \(y\).
- Swap \(x\) and \(y\).
If you consider the graph of a function, you get the graph of the inverse function by letting the \(x\)-axis and the \(y\)-axis swap places.
The graph of the inverse function \(f^{-1}(x)\), is the graph \(f(x)\) reflected in the line \(y=x\).
Not all functions have an inverse function. For some functions, swapping the axes will yield a curve that is not the graph of a function.
The function
\[f(x)=x^2,\]has two \(x\)-values corresponding to each positive \(y\)-value. If you let the \(x\)- and \(y\)-axis swap places, you get a curve having two \(y\)-values corresponding to each positive \(x\)-value. This curve cannot be the graph of a function.
Even if the function \(f(x)\) doesn't have an inverse, there is a similar function that has an inverse. The function
\[g(x) = x^2, x\ge 0\]has an inverse, and so does the function
\[h(x)= x^2, x \le 0. \]Range and domain
When talking about functions who only are defined for some \(x\)-values, it may be convenient to use proper terminology.
The domain of a function \(f(x)\)
is the set of all \(x\)-values
for which the function is defined.
The range of a function \(y=f(x)\)
is the set of all \(y\)-values
that the function takes.
If you let \(R_f\) denote the range and \(D_f\) the domain of a function \(f(x)\), then:
\[R_f=\left\{f(x): x\in D_f\right\}\]
For the function
\[f(x)=3+2\sin(x)\]we have that \(D_f = \mathbb{R}\) and \(R_f= [1, 5]\). Instead of writing the range using interval notation, we can write it using inequalities, as in \(R_f: 1\le y \le 5\). We can also write it more formally using set notation, as \(R_f = \{ y| 1\le y \le 5 \} \).
Restricting the domain
As we have seen, we must sometimes restrict the domain in order for a function to have an inverse. For the function
\[f(x) = x^2\]we can either restrict the domain to \(D_f: x\ge 0 \), in which case we get that \(f^{-1}(x)= \sqrt{x}\), or we can restrict the domain to \(D_f: x\le 0 \) and get that \(f^{-1}(x)= -\sqrt{x}\).
Since \(x\) and \(y\) are swapped when finding the inverse function, the domain of a function becomes the range of the inverse function, and the range becomes the domain.
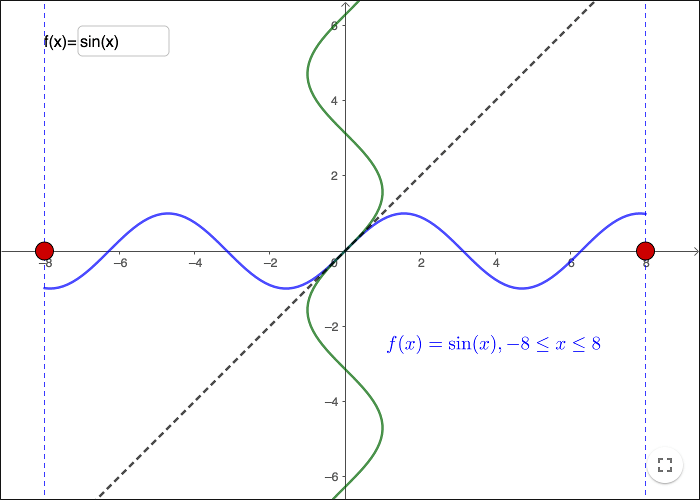
When it comes to periodic functions, there are infinitely many ways to restrict the domain.
In the worksheet above you can see that there are several ways of restricting the domain of \(\sin(x)\) in order to enable the definition of an inverse. As an example, you can restrict \(x\) to \(\frac{\pi}{2}\le x \le \frac{3\pi}{2} \). In that case the inverse function gets the range \(\frac{\pi}{2}\le y \le \frac{3\pi}{2} \) and the domain \(-1\le x \le 1\).
By convention the range and domain of inverse trigonometric functions are defined like this:
| function | domain | range |
|---|---|---|
| \(\arcsin x\) | \(-1\le x \le 1\) | \(-\frac{\pi}{2}\le y \le \frac{\pi}{2}\) |
| \(\arccos x\) | \(-1\le x \le 1\) | \(0\le y \le \pi\) |
| \(\arctan x\) | \(x \in \mathbb{R}\) | \(-\frac{\pi}{2}\lt y \lt \frac{\pi}{2}\) |
The inverse trigonometric functions are written asin, acos and atan in GeoGebra and in most programming languages.
Composite functions
A composite function is a function of a function. You use the symbol \(\circ\) to denote a composite function, as in:
\[(f\circ g)(x)=f(g(x))\]
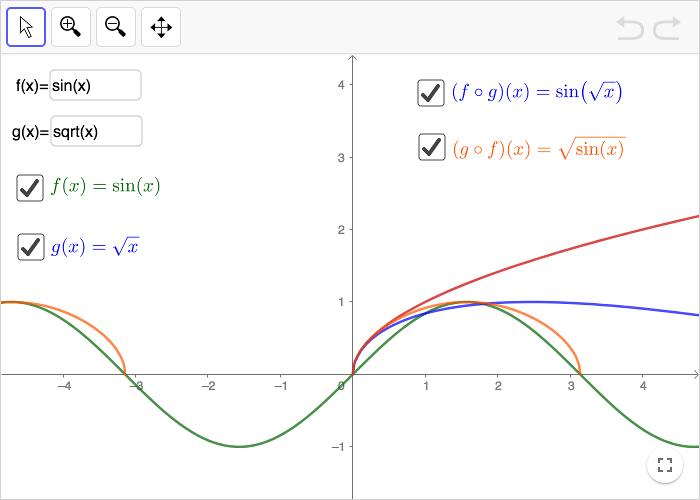
In GeoGebra it is easy to make composite functions. If you have defined two functions \(f(x)\) and \(g(x)\), you can write
f(g(x))
to make the composite function \(h(x) = (f \circ g)(x)\). You write
g(f(x))
to make the composite function \(p(x) = (g \circ f)(x)\).
Range and domain of composite functions
Consider the function
\[f(x) = 2^{\sqrt{4\sin x}},\]which can be seen as the composition of several functions. In order to find the range and domain, we can start by studying the graph.
The range of the function seems to be the interval \([1,4]\). The domain is clearly not \(\mathbb{R}\).
Of the functions \(g(x) = 2^x \), \(h(x) = \sqrt x\) and \(p(x) = 4\sin x\), only \(h\) has a domain that isn't \(\mathbb{R}\). In the composite function \( f = g \circ h \circ p\), the range of \(p\) is the domain of \(h\).
The range of \( p(x) = 4\sin(x)\) is the interval \([-4,4]\) but since we cannot allow negative function values, the domain must be restricted. Since \(p\) is the innermost function, the domain of \(p\) is also the domain of the function \(f\).
\[D_f = \{x | 2n\pi \le x \le (2n+1)\pi, n \in \mathbb{Z} \}\]The range of \(p(x) = 4 \sin(x) \) now becomes \([0,4]\). This is the domain of \(h(x) = \sqrt{x}\).
Since \(h(x) = \sqrt{x}\) has the domain \([0,4]\), its range must be \([0, 2 ]\). This is the domain of \(g(x) = 2^x \).
Since \(g(x) = 2^x \) has the domain \([0, 2 ] \), its range must be \([1, 4] \). This is the range of the function \(f\).
\[R_f: [1, 4]\]Composition of a function and its inverse function
If both the domain and the range are \(\mathbb{R}\) for a function \(f(x)\), and if \(f(x)\) has an inverse \(f^{-1}(x)\), then:
\((f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x\).
As an example, consider
\[f(x)=3+2x \Longleftrightarrow f^{-1}(x)=\frac{x-3}{2}\].Then
\[(f\circ f^{-1})(x)=f(f^{-1}(x))=f(\frac{x-3}{2})=3+2\frac{x-3}{2}=x\]
and
\[(f^{-1}\circ f)(x)=f^{-1}(f(x))=f^{-1}(3+2x)=\frac{3+2x-3}{2}=x\]
If the domain or the range of \(f(x)\) is restricted, then the composition of the function and its inverse is also \(x\), but only on an interval.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License