Triangle Definition
Similar triangles have been used throughout history to estimate distances that cannot be measured directly. Before calculators or computers were used, they used various forms of trigonometric tables that contained the sides of triangles for different angles.
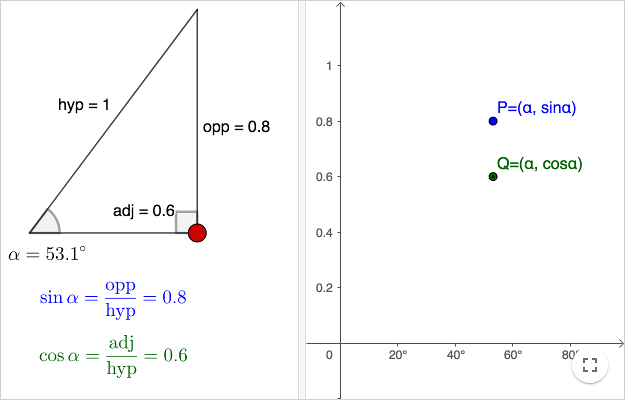
Definition of sine and cosine using a right-angled triangle
Using the labels in the picture above, the trigonometric functions are defined as
\[ \begin{align} \sin \alpha &= \frac {\text{opp}}{\text{hyp}} \\ \cos \alpha &= \frac {\text{adj}}{\text{hyp}} \\ \tan \alpha &= \frac {\text{opp}}{\text{adj}} = \frac{\sin \alpha}{\cos \alpha} \end{align} \]The abbreviations stand for hypotenuse, opposite and adjacent (relative the angle \(\alpha\)).
Since the ratio between two sides of a triangle does not depend on the size of the triangle, we can choose the convenient size given by the hypotenuse one. If the hypotenuse is constant, we can make two functions sine and cosine of the angle \(\alpha\). In order for \(\alpha\) to be one of the non-right angles in a right-angled triangle, we must have that \(0 \lt \alpha \lt 90^\circ\).
Reciprocal trigonometric functions
There are six different ratios between two sides in a triangle. The three most common ratios are sine, cosine and tangent. All ratios have a name, the three other ratios are called cosecant (\(\csc \)), secant (\(\sec \)) och cotangent (\(\cot \)). These ratios are defined like this:
\[\csc \alpha = \frac {\text{hyp}}{\text{opp}} = \frac{1}{\sin \alpha}\]
\[\sec \alpha = \frac {\text{hyp}}{\text{adj}} = \frac{1}{\cos \alpha} \]
\[\cot \alpha = \frac {\text{adj}}{\text{opp}} = \frac{1}{\tan \alpha}\]
Some historic tables
Nowadays we can use a calculator or a computer to find the values of trigonometric functions. And, unless we are particularly inquisitive, we don't have to know how a computer finds the value of sine for some angle. Historically they used tables of trigonometric ratios.
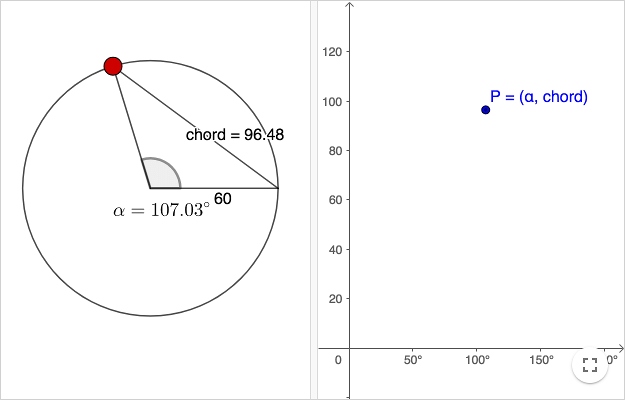
Tables of chords in ancient Greece
The first known trigonometric table was made by Hipparchus ( ≈ 150 BC ) who is also considered to be the father of trigonometry. Hipparchus original work has not survived but he is referenced in the book Almagest by Ptolemy ( ≈ 150 AD ). In Almagest there is a trigonometric table of chords. A chord is a segment whose endpoints are on a circle. Ptolemy used base 60 and he measured angles using degrees. The radius of the circle used in the table was therefore 60.
The chord as a function of the angle, which is graphed in the worksheet above, is an anachronism (just as the worksheet itself). Graphing functions was first done many centuries after Ptolemy.
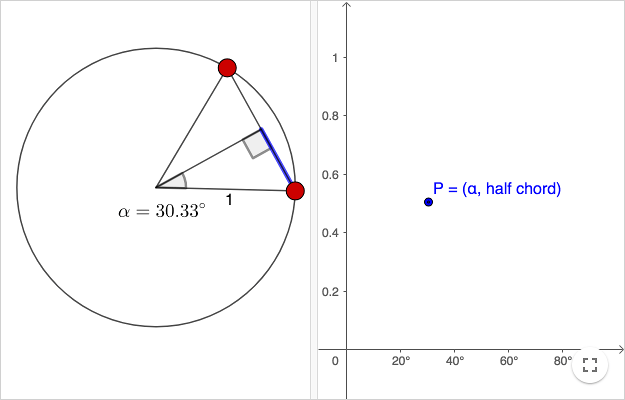
Tables of half-chords in India
The Indian mathematician Aryabhata ( ≈ 500 AD ) was the first to make a table using half-chords instead of chords. When using chords, the triangles are isosceles. When using half-chords, the triangles are right angled.
Etymology of the word sine
Aryabhata called these half-chords ardha-jya (in Sanskrit), which was abbreviated to jya. From this word, the Arabs coined the term jiba which means half-chord. Since vowels were omitted, the word jiba was written jb. When mathematics/science returned to Europe (≈ 1 K years after Ptolemy), the European scholars thought that jb stood for the Arabic word jaib, which means "cave" or "bay". They then translated the wrong word to the Latin word sinus.
Exact Angles
The exact values of sine and cosine for the angles \(30^\circ, 45^\circ\) and \(60^\circ \); can be derived from the triangles in the picture below.
Apart from these well know angles, there are also other angles that yield exact values of sine and cosine. In his book Almagest, Ptolemy gives the chords for the angles \(36^\circ \) and \(72^\circ \).
The golden triangle
The numbers \(36, 72\) and \(108\), have the properties that \(2\cdot 36 = 72\) and \(3\cdot 36 = 108\). Furthermore: \[72+108=72+72+36=108+36+36=180\]
Starting with the isosceles triangle to the left in the picture below, you can construct two isosceles triangles by bisecting one of the \(72^\circ \) angles.
Considering the interior angles of a regular pentagon
one can form a variety of self-similar patterns using pentagons and pentagrams that contain the angles \(36^\circ, 72^\circ, 108^\circ\) - and no other angles.
The triangle is called the golden triangle since the ratio between the sides is the golden ratio.
Exercises
Exercise 1
Use similarity to set up a quadratic equation for \(x\) (using the notation from the picture to the right). By solving the equation, show that the ratio of the sides in the golden triangle is the golden ratio.
Exercise 2
Find the exact values of \(\cos 36^\circ \) and \(\cos 72^\circ \).
Extending the definitions
The trigonometric ratios can be seen as functions of an angle. The graphs of such functions are drawn in the applets above. If the angle is called \(x\), the functions are defined for \(0\lt x \lt 90^\circ\), otherwise \(x\) cannot be a non-right angle in a right-angled triangle. We can extend the definition of the trigonometric functions so they are defined for all \(x\). When making such a definition, a unit circle is used instead of a triangle.
animated gifs:
Pentagrams on tumblr.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License