Music

The Sound of Sine

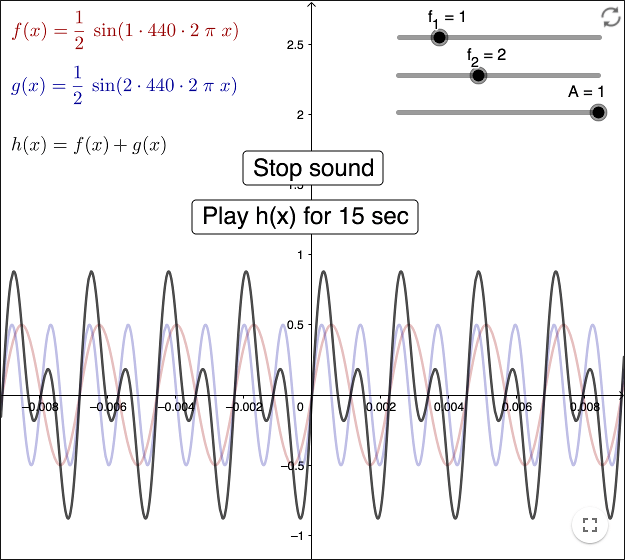
The note A (A₄) has the frequency \(f=440\) Hz, which means that it has the angular frequency \(\omega = 440\cdot 2\pi \) rad/s. If you want to play sine waves, you can use that frequency as a base, as in the worksheet below.

Load GeoGebra worksheet

Note that if the functions \(f\) and \(g\) have different frequencies, then you can clearly hear that the wave \(h\) is made of two waves.

Play music in GeoGebra

You can play music in GeoGebra, play notes using different instruments, and play the sound of a function. The function is assumed to be a function of time and the function values must be between -1 and 1.

Let's say you want to play a single sine function. First make a slider \(f\) using the tool Slider. The slider is used for frequency values. Enter the function sin(f*440*2*pi*x). The function will be called \(g\).

In order to see the fluctuations of the sine function, choose the tool Move the Graphics View. Then drag the \(x\)-axis to rescale the coordinate system.

To play the function \(g\) between 0 and 15 seconds, use the tool Button to make a button and enter the code

PlaySound(g, 0, 15)

as GeoGebra Script. Select the tool Move. Try clicking the button and changing the frequency!

To turn off the sound being played, use the command:

PlaySound(false)

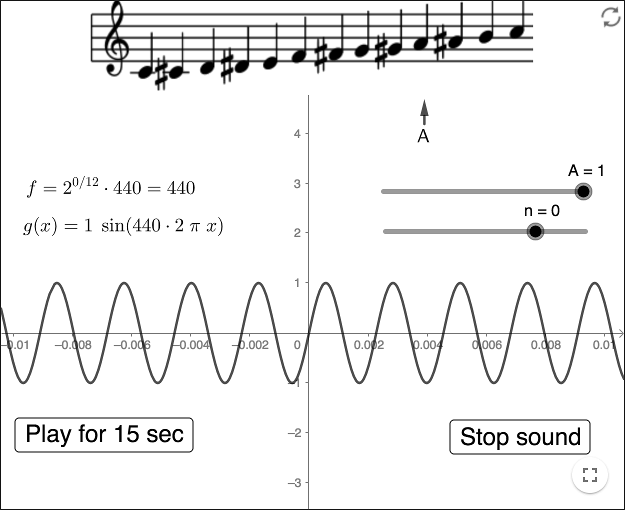
The frequencies of the notes

An octave is a doubling of frequencies. When the frequency 440 Hz is doubled to 880 Hz, you go from the note A₄ to the note A₅, where A₅ is in the next octave. An octave is divided into twelve notes, seven of these are C, D, E, F, G, A, B; the white keys on a piano. Some countries use other names for the notes.

The frequencies of the twelve notes are in a geometric progression. This means that the ratio of the frequency of two consecutive notes is constant. When going from the frequency of one note to the next, you multiply with the same factor for all notes. After 12 such multiplications, you should have doubled the frequency. If that factor is denoted by \(a\), we can find the factor from:

\[a^{12}=2 \Leftrightarrow a=2^{\frac{1}{12}}\]

Load GeoGebra worksheet

Some countries use other notations for the notes than the ones seen below the arrow in the applet above.

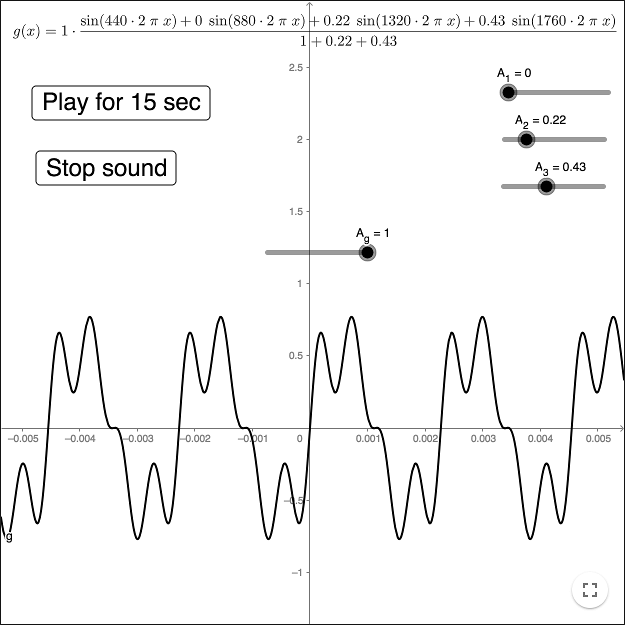
Overtones

The reason why different instruments sound different when playing the same note, is that they don't play one single sine wave. An instrument in general also plays a number of overtones, and these overtones may vary between different instruments. An overtone is a tone having a higher frequency than the note being played.

If you consider a string of a guitar, then the length of the string (measured by where you hold down a finger) decides what frequencies you hear since the string is attached at both ends. Mathematically, this corresponds to dividing half a period by an integer, which means multiplying the angular frequency by an integer.

In the worksheet below you can add three overtones by letting their respective amplitude increase from zero.

Load GeoGebra worksheet