Waves

A sine wave is a function of the time \(t\):

\[y(t)=A\sin(\omega t - \phi)\]

The phase of a sine wave, \(\phi\), is the displacement of the wave when \(t=0\).

The angular frequency of a sine wave, \(\omega\), has the unit rad/s.

The frequency of a sine wave, \(f\), denotes how many revolutions there are per unit time. The unit for frequency is Hz=1/s (Hertz). The correspondence between angular frequency and frequency is:

\[\omega= 2\pi f\]

A one-dimensional sine wave that propagates in space, is a function of two variables \(x\) and \(t\), where \(x\) is the position and \(t\) the time.

\(k\) denotes the speed of propagation, i.e. how fast the wave is propagating.

The difference between changing the speed of propagation and changing the frequency, when a wave is played as music, is demonstrated in the recording below.

The wave shown in the recording is not a simple sine wave but a superposition of waves.

Superposition of Waves

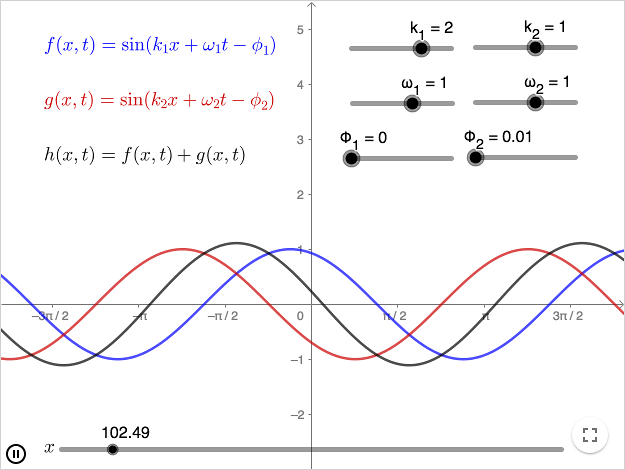
The superposition principle of waves is: the resulting wave formed by several waves overlapping in space and time, can be found by adding the waves.

Load GeoGebra worksheet

When \(k_1=2\) and \(k_2=1\), the red wave propagates twice as fast as the blue wave.

If the waves move with the same speed of propagation but in opposite directions (\(k_1=-k_2\)), and if they have the same angular frequency (\(\omega_1=\omega_2\)), then the resulting wave is a standing wave.

If the waves move with the same speed of propagation and in the same direction (\(k_1=k_2\)), and if they have the same angular frequency, then they cause interference. If the waves have the same phase, they cause constructive interference, i.e. the amplitude of the resulting wave is the sum of the amplitudes. If one of the waves is shifted by \(\phi=\pi\), then they cause destructive interference.