From Eratosthenes to Stellar Parallax
Eratosthenes ≈ 200 BC, the size of the earth
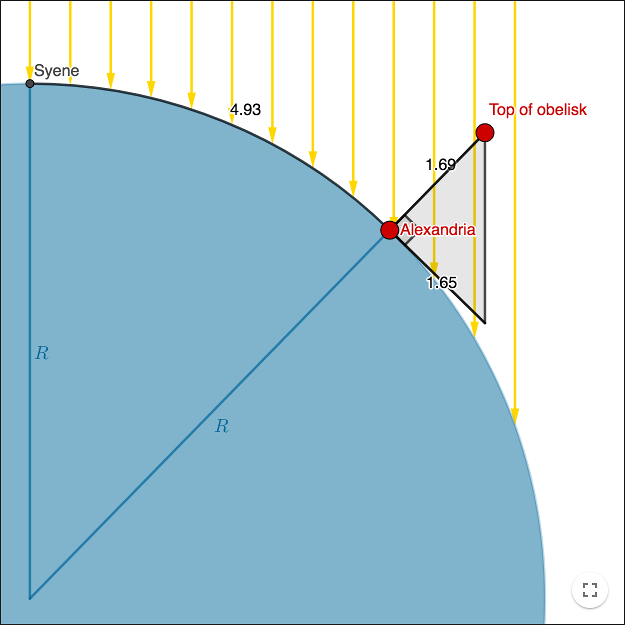
Eratosthenes was librarian at the Royal Library of Alexandria. He read in a book that every summer solstice at noon, the water deep down in a well in Syene was all illuminated by the sun. He realized that at that moment the sun appeared at the zenith, directly above the well. At the same time in Alexandria the sun cast shadows. Alexandria and Syene are at about the same meridian, Alexandria is north of Syene. Eratosthenes estimated the distance between Syene and Alexandria. Then he measured the shadow of an obelisk of known height in Alexandria, on the summer solstice at noon, and calculated the circumference of the earth.
Exercise
Estimate the size of the earth by using Erathostenes' method
The unit in the worksheet is 1000 km. The real distance between Syene and Alexandria is approximately 1000 km (i.e. 1 in the worksheet). For simplicity, let's assume that the distance is longer and that the obelisk is a couple of thousands km high.
When measuring the shadow of the obelisk, the distance is measured along the surface of a sphere and doesn't really form a right-angled triangle as in the worksheet. If the picture was to scale though, the error from approximating with a right-angled triangle, would be less than any other error in the measurements.
Find the radius of the circle in the worksheet (the earth).
Ptolemy ≈ 150 AD, the universe
Aristotle (≈350 BC) described the universe as spheres with the earth as the center; all objects in the sky were attached to the spheres and moved in circles around the earth. Some observations of the sky were correctly explained by that model but not all.
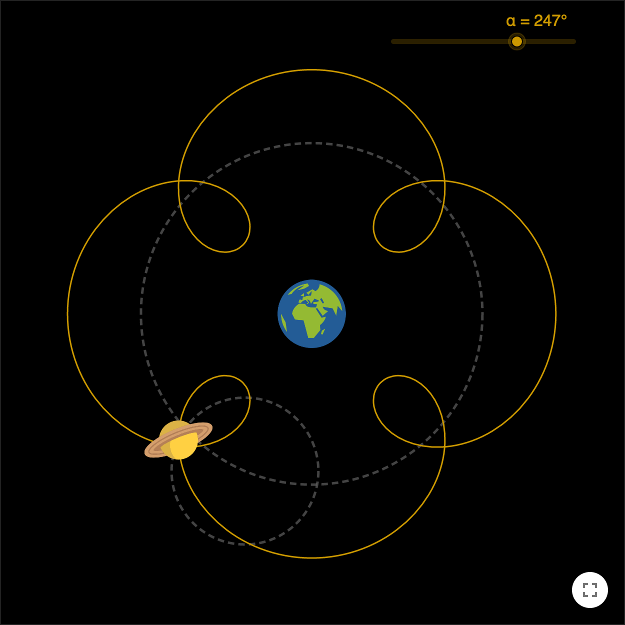
Ptolemy came up with a different model were the distant objects were attached to, not the spheres themselves, but circles lying on the spheres, so called epicycles. This model could account for the motions observed at the earth.
By keep attaching epicycles on epicycles on epicycles...any planetary motion can be explained, in fact any orbit can be constructed.
Tycho Brahe 1546-1601, planetary motion
Tycho Brahe built instruments to observe celestial bodies. Using his instruments, he could measure angles to an accuracy that had not been possible in the past. He built quadrants and sextants; using these instruments and a compass he could, among other things, measure the heights of celestial bodies above the horizon. Tycho Brahe's observations were later used by Johannes Kepler who used the data to discover the laws of planetary motion.
Quadrants, sextants and octants
A quadrant is a quarter of a circle. Using a quadrant one can measure the height above the horizon of a celestial body. Tycho Brahe built a large mural quadrant at the wall of his observatory Uranienborg.
A sextant is one sixth of a circle. Guess what an octant is!
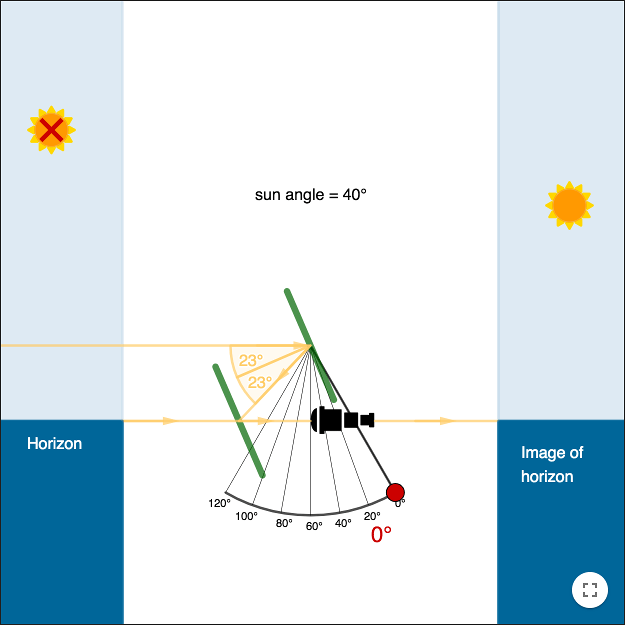
If the angle of the sun is 40°, the upper green mirror should be rotated 20°.
Since two angles are used, the angle of incidence and angle of reflection, the angle of rotation must be doubled to yield the angle of the sun. Hence the strange grading og the sextant.
Tycho Brahe and geocentrism
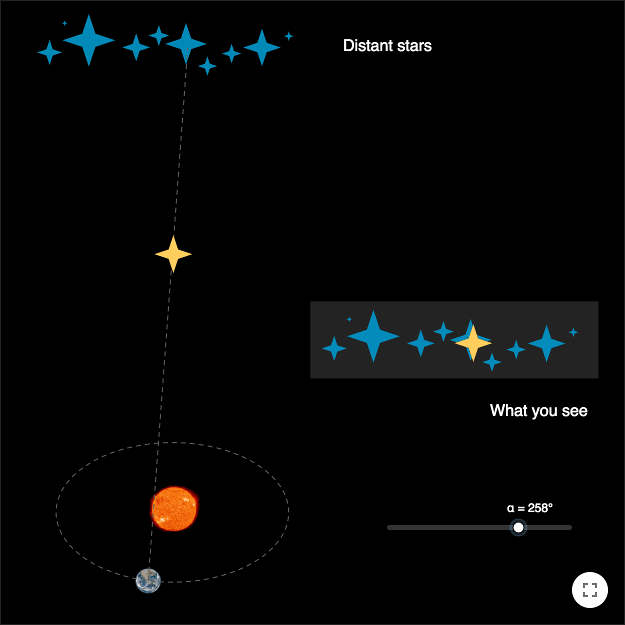
Tycho Brahe would only believe in what he could observe. Since he could not observe any stellar parallax, he concluded that the earth did not move. Another explanation for him not seeing any stellar parallax could be that the stars were too far away, making an angle even smaller than the angles Tycho Brahe could measure. It would take another couple of centuries before a stellar parallax could be observed.
Stellar Parallax
A parallax is a phenomenon caused by observing an object from two different observation points, e.g. two eyes. If you hold up a finger and close your right eye and then close your left eye, it will look as if the finger moves relative to the background.
In order to get a parallax when viewing a faraway object, like a star, the two observation points must not be close to each other.
The first stellar parallax was observed in 1838 by Friedrich Bessel. He found that the star 61 Cygni had a parallax of 0.314 arcseconds, i.e. that the angle subtended by the star as the earth orbits the sun is 0.314/3600 degrees.
The unit for measuring the distance to stars is parsec, the parallax of one arcsecond.
references:
Globe-icon from: Free Icons Library: Glove Icon SVG #399087.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License