Normalfördelning
Från diskret till kontinuerlig
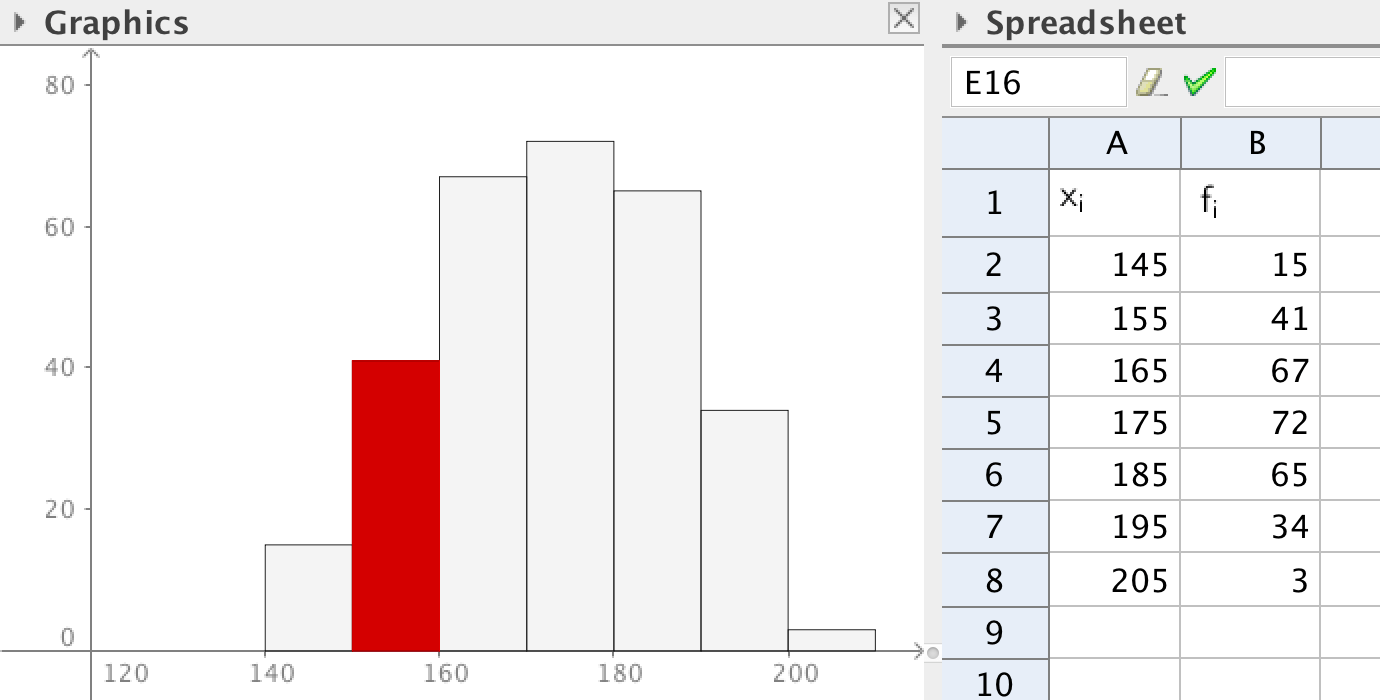
Sannolikheten att en slumpvis vald person har en längd mellan 150 och 160 cm kan beräknas ur tabellen:
\[p=\frac{41}{15+41+67+72+65+34+3}\]
Man kan också beräkna sannolikheten genom att betrakta areor i stapeldiagrammet. Sannolikheten fås som arean av den röda stapeln delat med den totala arean.
\[p=\frac{41\cdot 10}{15\cdot 10+41\cdot 10+67\cdot 10+72\cdot 10+65\cdot 10+34\cdot 10+3\cdot 10}\]
Sannolikhet och area
Ett sätt att representera sannolikheten att ett utfall hamnar i ett intervall, är att låta intervallets area motsvara sannolikheten. Den totala arean måste då vara ett. Stapeldiagrammet kan normeras så att den totala arean blir ett.
Övning 1
Lägg till ännu en kolumn i kalkylbladet som motsvarar den relativa frekvensenz.
Du kan addera ett antal värden i celler genom att skriva:
Sum(B2:B8)
Om man gör ett stapeldiagram över den relativa frekvensen istället för den absoluta frekvensen så kommer den totala arean fortfarande inte att bli ett. Lägg därför till ännu en kolumn i kalkylbladet för att normera de relativa frekvenserna. Hur skall denna kolumn konstrueras? Kolumen för datan skall inte ändras. Rita upp stapeldiagrammet!
Övning 2
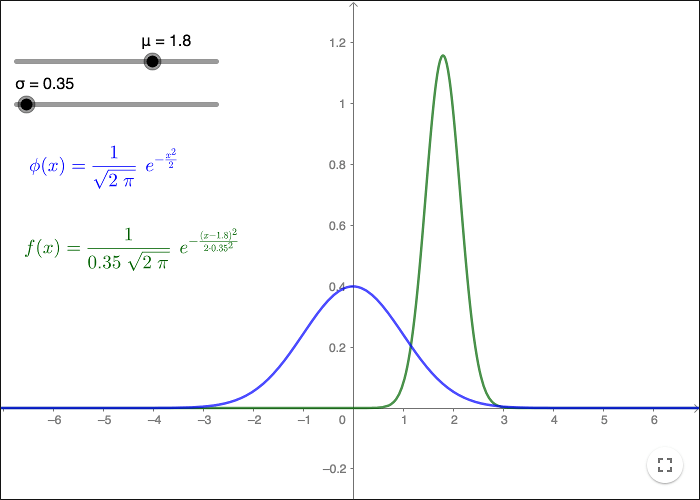
Man kan approximera en diskret fördelning med en kontinuerlig funktion. En sådan approximerande funktion är normalfördelningens täthetsfunktion. Grafen till normalfördelningens täthetsfunktion är en helt symmetrisk klockformad kurva vars utseende bara beror på två variabler, medelvärdet och standardavvikelsen.
Om \(\mu\) är medelvärdet och \(\sigma\) standardavvikelsen, så är normalfördelningens täthetsfunktion:
\[f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\left( - \dfrac{(x-\mu)^2}{2\sigma^2}\right)} \]
Använd medelvärdet 173.2492 och standardavvikelsen 14.0333 till att plotta grafen till normalfördelningen.
Standardiserad normalfördelning
Fördelningsfunktionen för den standardiserade normalfördelningen \(\phi\), har medelvärdet \(\mu =0\) och standardavvikelsen \(\sigma=1\).
\[\phi (x)=\frac{1}{\sqrt{2\pi }} e^{-\frac{1}{2}x^2} \]
Att en variabel \(X\) är normalfördelad med medelvärdet \(\mu\) och standardavvikelsen \(\sigma\), betecknas \(X\ \sim \mathcal{N}(\mu,\sigma^2)\). En variabel som är fördelad enligt den standardiserade normalfördelningen betecknas \(Z\). Sambandet mellan \(Z\) och \(X\) är
Sannolikheten ges av arean under kurvan. Den totala arean är därför alltid ett. Om sannolikheten för en normalfördelad variabel \(X\) betecknas \(P\), får man att
\[P(a\lt X \lt b)=\int_a^bf(x)dx\]
där \(f(x)\) är normalfördelningens täthetsfunktion.
Normalfördelning i GeoGebra
Med verktyget
Sannolikhetskalkylator,
kan du beräkna sannolikheten mellan valfria gränser för en mängd fördelningsfunktioner. Verktyget finns i den meny som hör till kalkylbladet.
Det omvända normalfördelningsproblemet
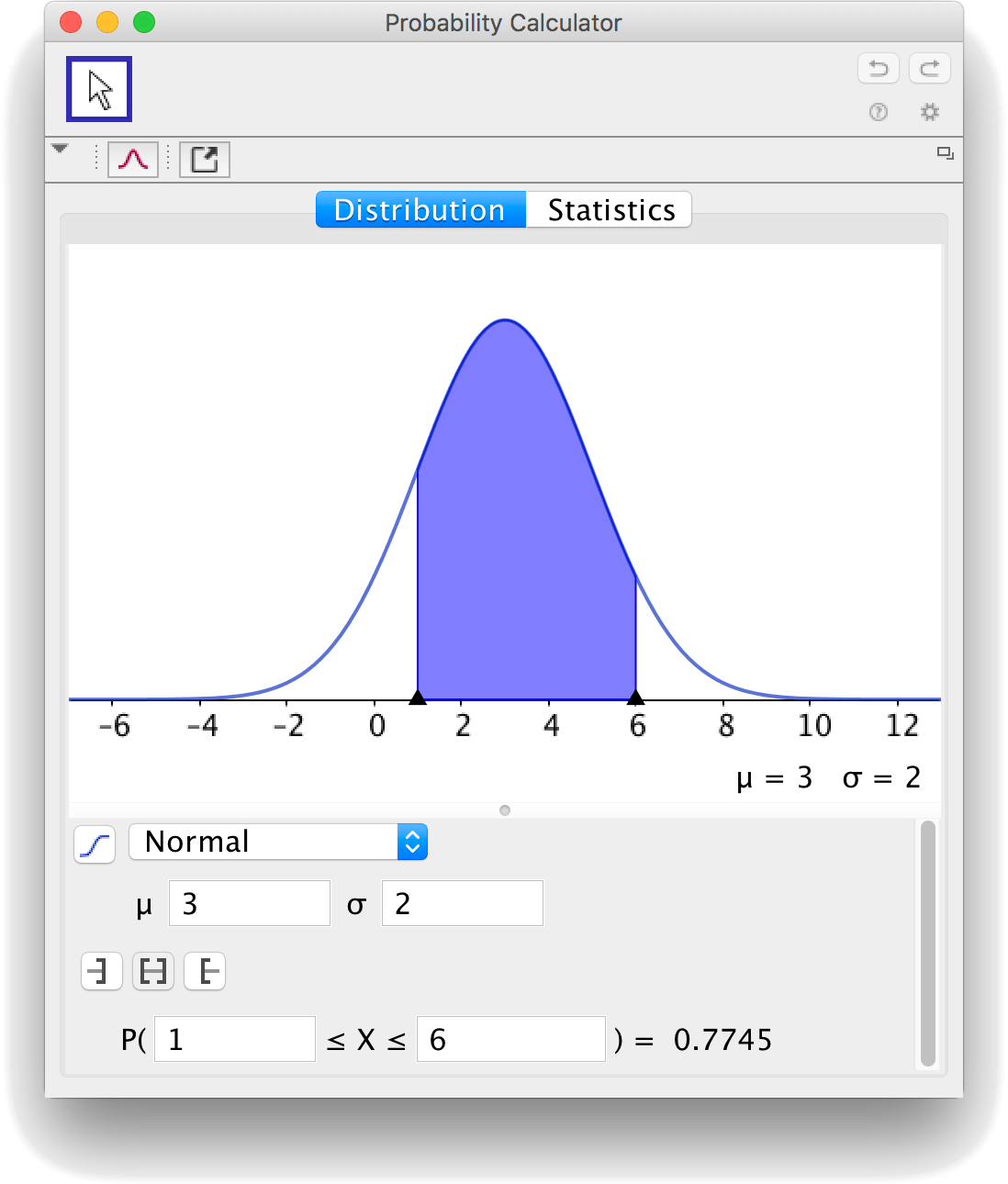
Om man känner till medelvärdet och standardavvikelsen, så kan man beräkna sannolikheten för givna gränser med Sannolikhetskalkylatorn.
Det omvända problemet är att man känner till sannolikheten för givna gränser och vill beräkna medelvärdet och standardavvikelsen. Eftersom det är två okända som skall bestämmas, krävs det att man känner till två sannolikheter.Problemet löses genom att man gör en jämförelse med den standardiserade normalfördelningen.
Antag att du vet att \(P(X\lt 4)=0.4\) och att \(P(X\lt 3)=0.2\). Gränserna \(4\) och \(3\), kan jämföras med motsvarande gränser för den standardiserade normalfördelningen. Sambandet mellan dessa gränser ges av \(z=\frac{x-\mu}{\sigma}\), där \(z\) är gränsen för den standardiserade normalfördelningen, och \(x\) är gränsen för den okända normalfördelningen.
För att bestämma de gränser som motsvaras av gränserna \(4\) och \(3\), kan du använda GeoGebra. Det gäller att bestämma \(z_1\) ur sambandet \(P(Z\lt z_1)=0.4\) och \(z_2\) ur sambandet \(P(Z\lt z_2)=0.2\).
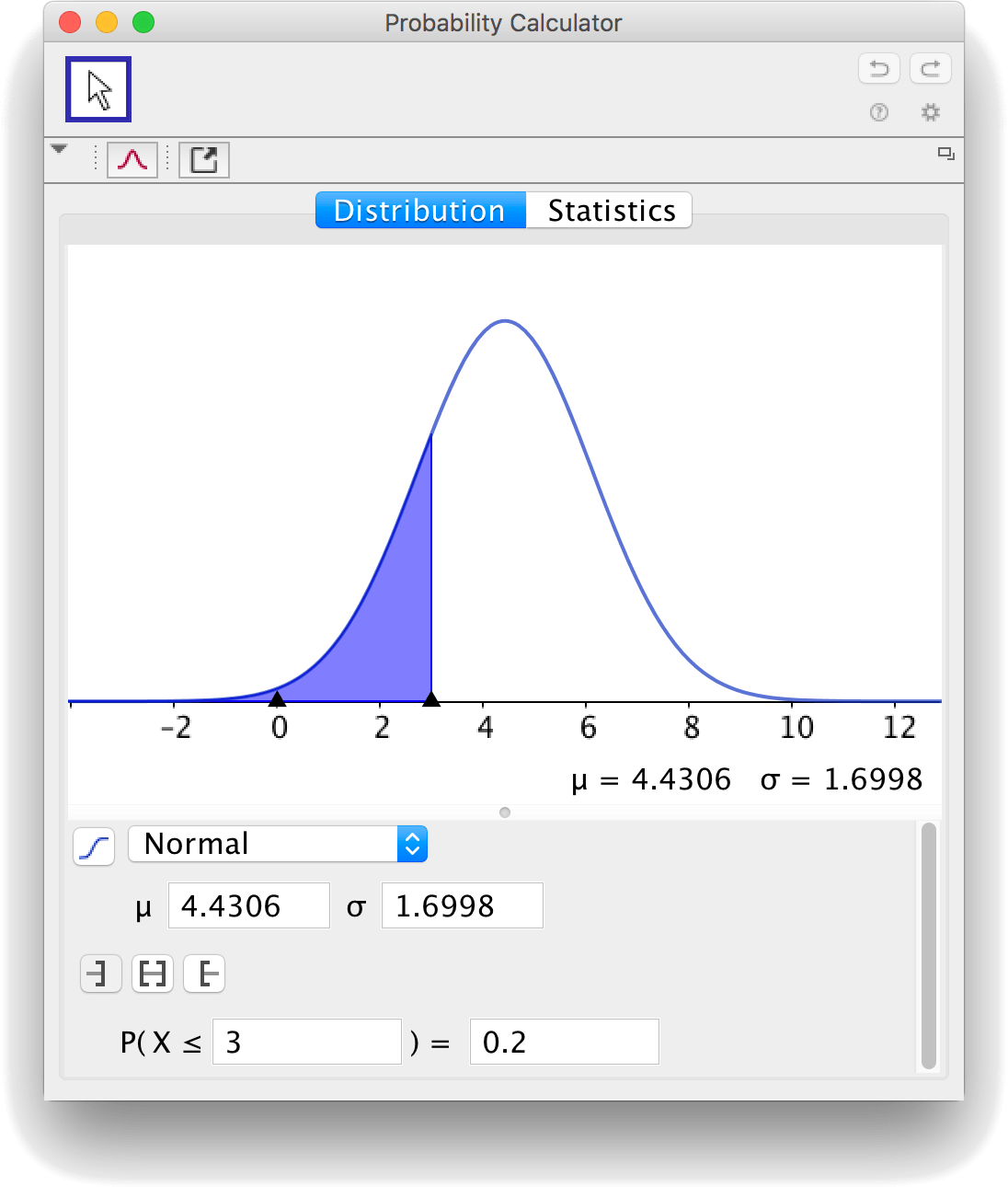
Skriv in 0.4 i rutan för sannolikheten och tryck enter. Du får att \(z_1=-0.2533\).

På motsvarande sätt får du att \(z_2=-0.8416\). För att bestämma \(\mu\) och \(\sigma\), löser du ekvationssystemet:
\[\left\{ \begin{align*} -0.2533&=&\frac{4-\mu}{\sigma} \\ -0.8416&=&\frac{3-\mu}{\sigma} \end{align*} \right. \]
Lösningen är \(\mu=4.4306\) och \(\sigma=1.6998\). Lösningen kan kontrolleras i Sannolikhetskalkylatorn.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License