Medelvärde och standardavvikelse
Stapeldiagram
Om du har en frekvenstabell kan du göra ett stapeldiagram. Börja
med att skriva in följande data i kalkylbladet. Mittvärdet av det första intervallet är 145. Skriv
in 145 i A1. Skriv in =A1+10 i A2 och tryck enter. Gör relativa kopior genom att dra i den
lilla blå kvadraten i det nedre högra hörnet av A2
| Height (cm) | Frequency |
|---|---|
| 140-150 | 15 |
| 150-160 | 41 |
| 160-170 | 67 |
| 170-180 | 72 |
| 180-190 | 65 |
| 190-200 | 34 |
| 200-210 | 3 |
Du behöver två listor, en datalista och en frekvenslista. Gör en lista per kolumn.
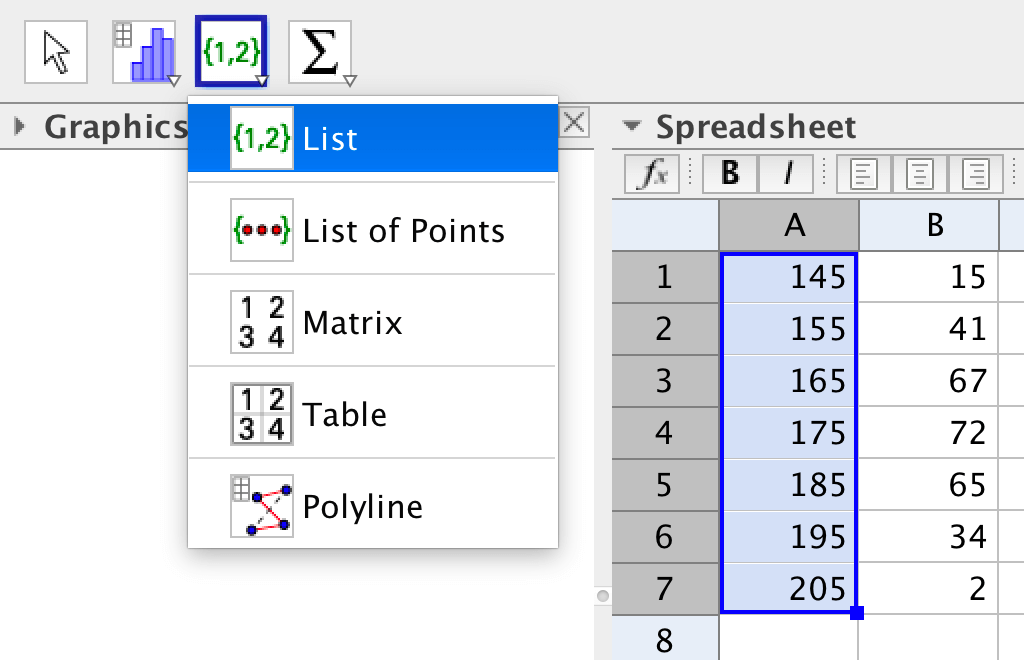
För att göra ett stapeldiagram använder du kommandot:
Stapeldiagram[namnet på datalistan, namnet på frekvenslistan]
Talen i datalistan måste öka med en konstant term.
Notera att om du skriver in ett kommando i kommandoraden och trycker F1 så får du hjälp.
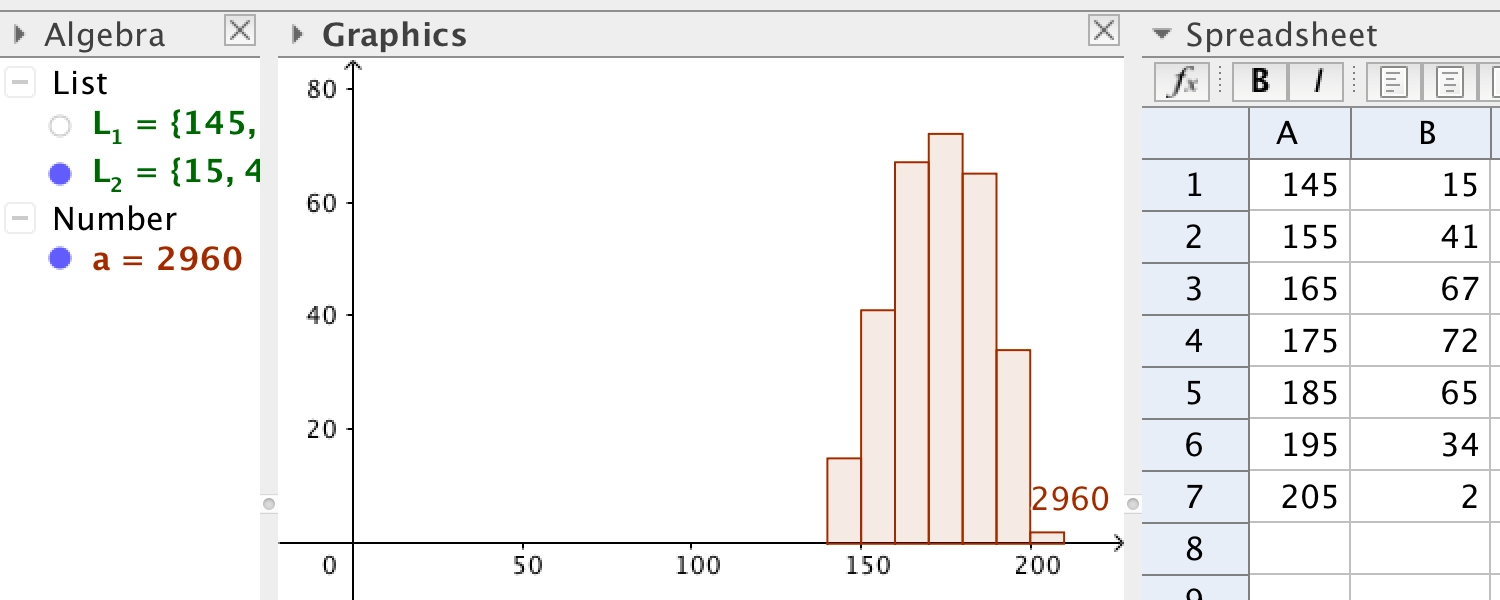
Stapeldiagrammet i bilden ovan kallas \(a\), värdet på variabeln \(a\) är stapeldiagrammets area.
Då man har en frekvenstabell har man två kolumner, en datakolumn och en frekvenskolumn. Låt \(f_i\) beteckna frekvensen och \(x_i\) motsvarande data; formlerna för medelvärdet \(\mu\) och standardavvikelsen \(\sigma\) är:
där \(k\) är antalet data och \(n=\sum_{i=1}^{k}f_i\).
Väntevärde och varians
Om en slumpvariabel \(X\) kan anta värdena \(x_i\) med sannolikheterna \(p_i\), så kallas det mest troliga värdet för väntevärdet \(E[X]\).
\[E[X]=p_1x_1+p_2x_2+\ldots +p_kx_k=\sum_{i=1}^kp_ix_i\]
Värdet \(x_i\) avviker från medelvärdet \(\mu\) med \(|x_i-\mu |\). Av beräkningstekniska skäl, är det enklare att betrakta kvadrater än absolutbelopp, \((x_i-\mu)^2\). Det mest troliga värdet av kvadraterna på avvikelserna kallas variansen \(Var(X)\).
\[Var[X]=p_1(x_1-\mu)^2+p_2(x_2-\mu)^2+\ldots +p_k(x_k-\mu)^2=\sum_{i=1}^kp_i(x_i-\mu)^2\]
Om man har en frekvenstabell med datavärden \(x_i\) och frekvenser \(f_i\), och om \(n=\sum_{i=1}^{k}f_i\), så är \(p_i=\frac{f_i}{n}\) sannolikheten för utfallet \(x_i\). Från detta får man att:
Statistisk envariabelanalys
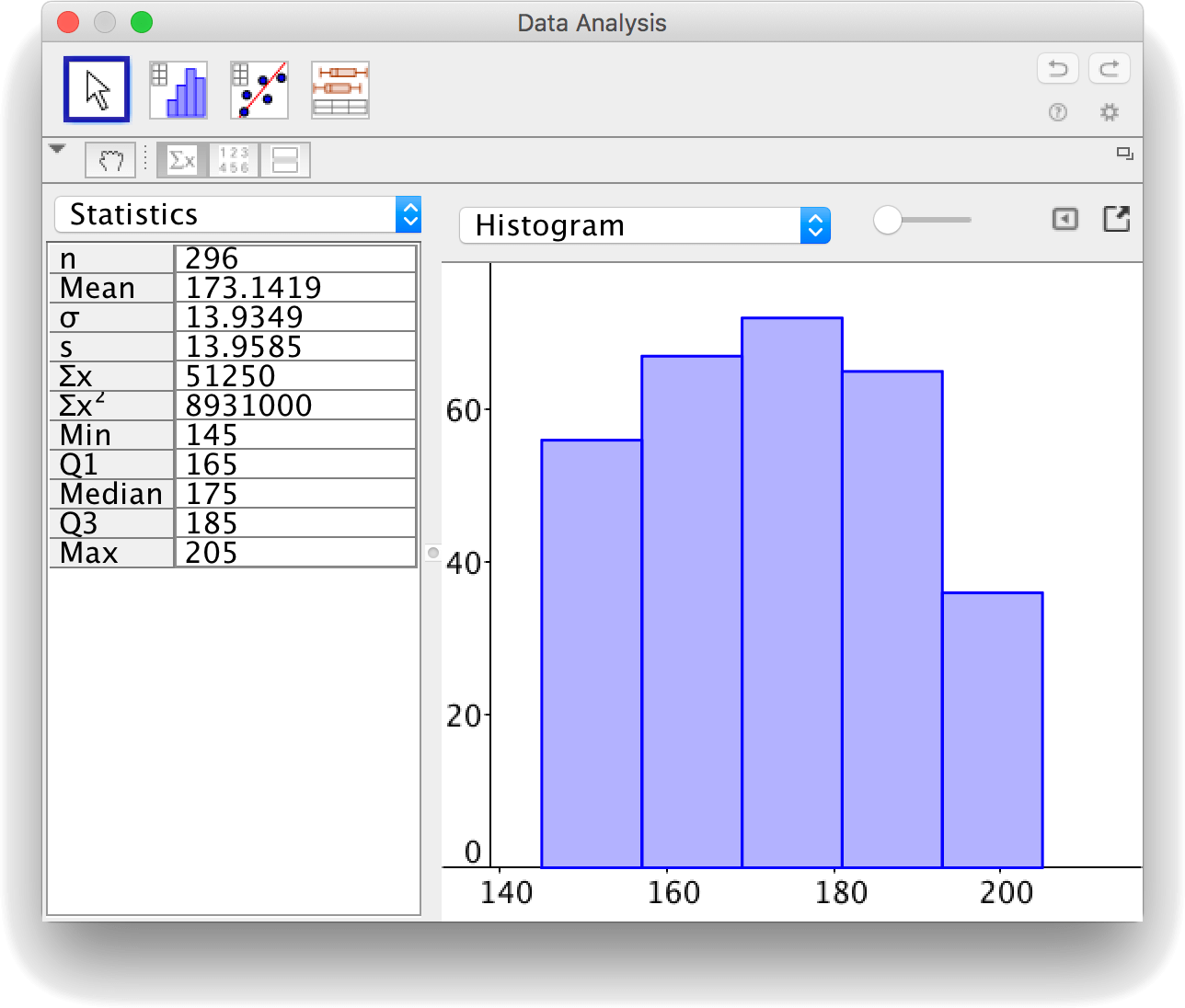
Från och med GeoGebra 4.0 kan man göra en statistisk envariabelanalys och på så vis bland annat få fram medelvärde och standardavvikelsen. GeoGebras verktyg kan användas på en kolumn av data eller på flera kolumner av grupperade data i ett kalkylblad. Den kan däremot inte användas på en frekvenstabell direkt. Om man har en frekvenstabell måste den göras om till en tabell av grupperade data.
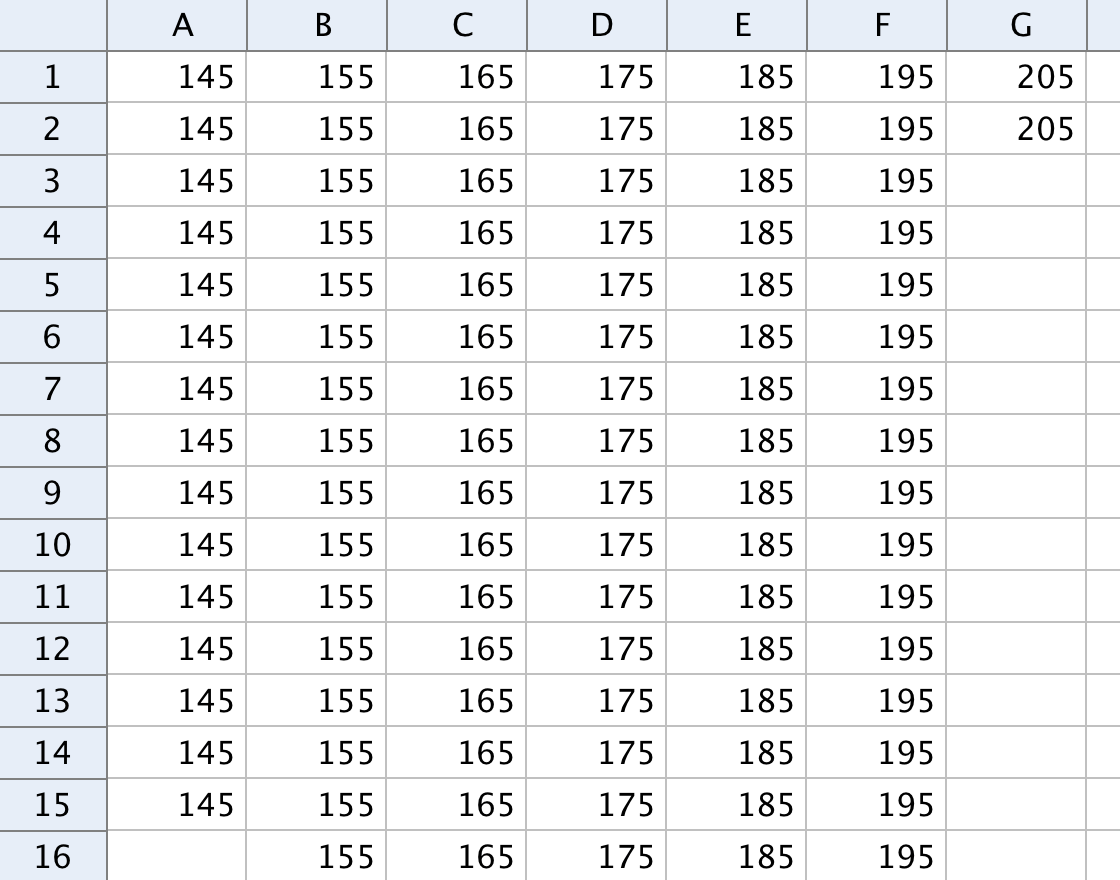
I bilden ovan innehåller kolumnerna A-G grupperad data.
Markera kolumn A-G och välj verktyget "One Variable Analysis".
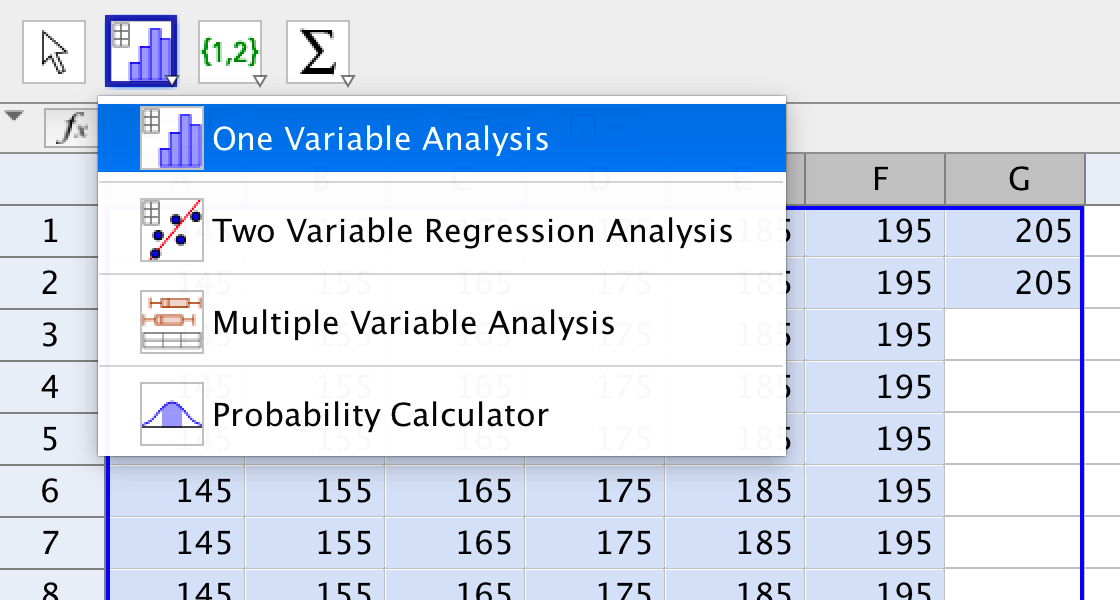
I det fönster som då dyker upp, hittar man bland annat statistiska mått som medelvärde och standardavvikelse.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License