Fractions
Integer area
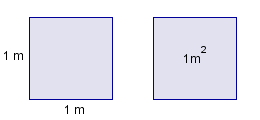
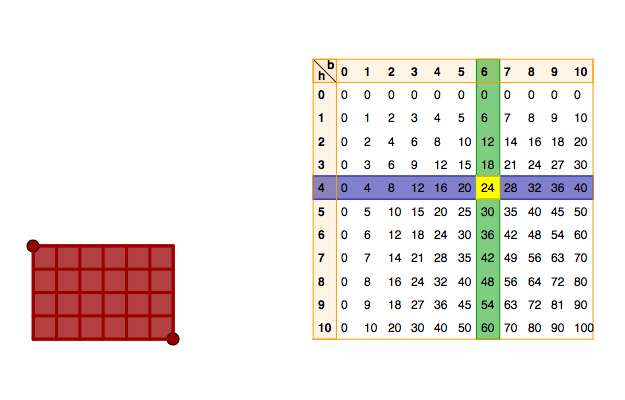
If you only use integers you can find the area of a rectangle by counting the number of squares. If one square has the base 1 m and the height 1 m, then the area is 1 m2 (one square metre).
In the general case you may not use specific units but just length units or area units respectively.
You get the area of a rectangle by multiplying the number of squares along the base with the number of squares along the height. If the area is called A, the number of squares along the base b and the number of squares along the height h; then the formula for the area is: \(A=b\cdot h\).
Fractions as areas
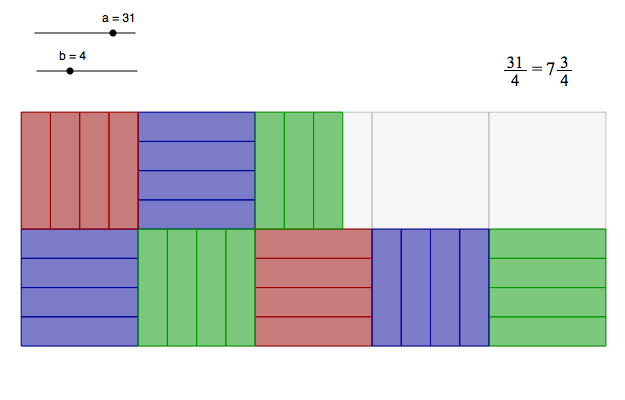
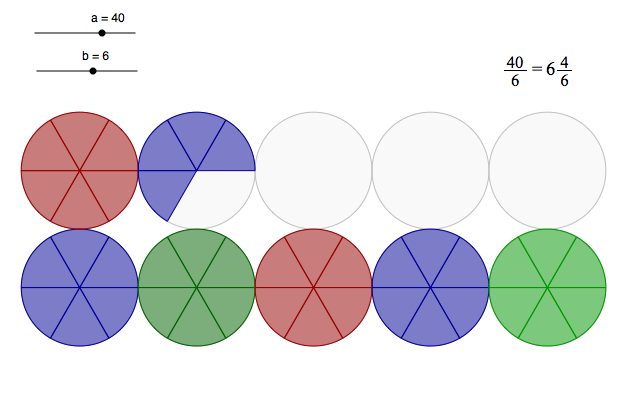
If you divide a unit area into three pieces, then each piece has the area one third (1/3) of an area unit; two pieces have two thirds (2/3) of an area unit. Seven thirds are more than two whole area units. You can write 7/3 in mixed form by finding out how many area units you have and how many thirds you have left. \[\frac{7}{3}=2\frac{1}{3}\]
The notation used in mixed form is confusing. There is no sign between 2 and 1/3, in this case it means that you should use a plus-sign, i.e. 2 + 1/3. In all other cases in mathematics, no sign means that you should use multiplication; i.e. 2x means 2·x.
Mixed form is tedious to use when the mathematics gets more complicated. You must know how to interpret the notation in order to read cook books but avoid mixed form when doing mathematics!
You can also visualize fractions as areas of pies ↓.
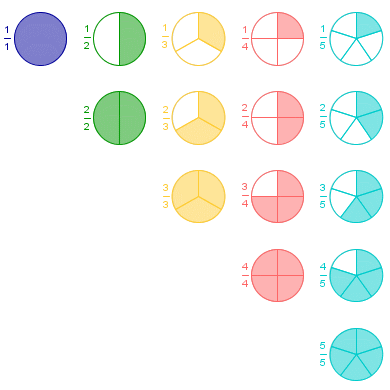
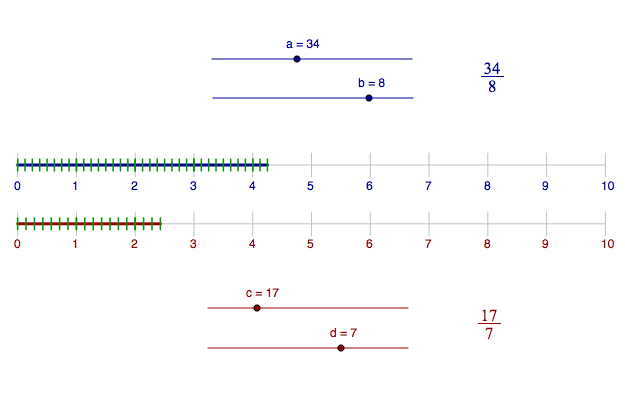
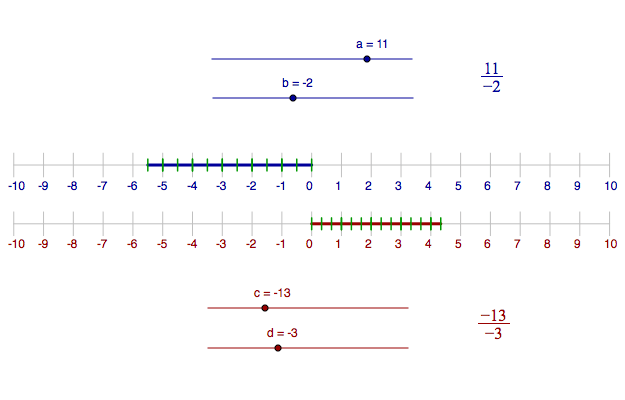
Fractions on the number line
Exercise 1
Let the upper number be 5/3. Find another fraction on the lower number line that is the same number.
Let the upper number be 2/5. Find another fraction on the lower number line that is the same number.
Let the upper number be 1/2. Find several other fractions on the lower number line that all are the same number.
Exercise 2
Let the upper number be 10/8. Find another fraction on the lower number line that is the same number.
Let the upper number be 9/3. Find two other fractions on the lower number line that are the same number.
Exercise 3
Write the number 10/13 as several other fractions. You can't use the applet above. How do you do?
Write the number 20/60 as another fraction where the numerator and denominator are as small as possible. You can't use the applet above. How do you do?
Negative Fractions
If you owe someone four fifths of a pie, you might say that you have -4/5 pie.
You can place the negative sign in front of the numerator instead of in front of the fraction: \[-\frac{4}{5}=(-1)\cdot \frac{4}{5}=\frac{(-1)\cdot 4}{5}=\frac{-4}{5}\]
If you have a negative sign in front of the numerator you can place it in front of the denominator (if you follow conventions you never have a negative denominator): \[\frac{-4}{5}=\frac{(-1)\cdot (-4)}{(-1)\cdot 5}=\frac{4}{-5}\]
If the denominator and the numerator are both negative, the fraction is positive: \[\frac{-4}{-5}=\frac{(-1)\cdot 4}{(-1)\cdot 5}=\frac{4}{5}\]
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License