Angles
This is an informal treatment. A formal treatment is given on next page: Summary - Angles.
Move and turn (turtle programming using Scratch)
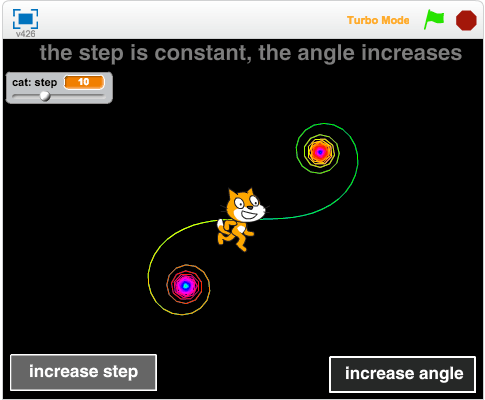
Turtle programming is when you program a turtle by giving it commands like "move" and "turn". By "moving" and "turning" you can make intricate patterns. Some easier patterns are shown below.
The pattern created when successively increasing the angle, is a so called Euler spiral (or Cornu spiral).
By "moving" and "turning" you can get acquainted with the concept angle.
The cat moves some steps and turns some angle.
Click on "increase step" to successively increase the step moved!
Click on "increase angle" to successively increase the angle turned!
Regular polygons and exterior angles
Angles can be used to measure rotations. One unit when measuring angles is degree (there are also other units for measuring angles). Degrees are denoted by °. If you rotate one revolution, you have rotated an angle of 360°. Half a revolution is 180°, a quarter of a revolution is 90°, and so on.
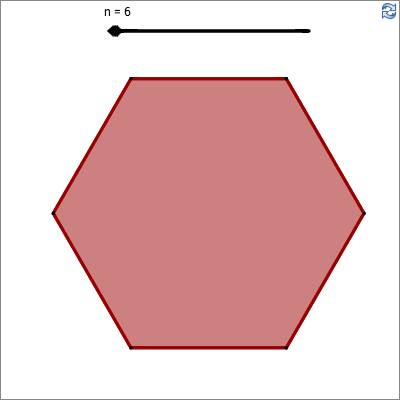
A regular polygon is a polygon in which all sides are the same length, and all angles are equal.
Scratch-task 1
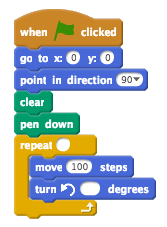
What numbers should be in the empty spaces (in the image to the right) if you want to draw a square?
After the square has been drawn, the sprite is back where i started, pointing in the same direction as it did to begin with.
What numbers should be in the empty spaces if you want to draw a regular triangle? The sprite should end up at its starting point, pointing to the right.
What numbers should be in the empty spaces if you want to draw a regular 5-sided polygon (a pentagon)?
How do you find the turning angle, in terms of n, when drawing a regular n-sided polygon?
Scratch-task 2
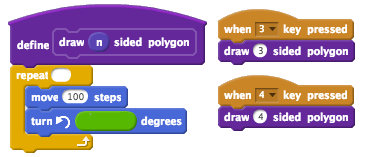
Make a block for drawing a n-sided polygon! Add number input n under Options. The parameter n can be used at any place where a block has a number as input.
Fill in the empty spaces that define the block. Use an operator to calculate the correct angle in terms of n!
Try out the polygon-block you just made using various values for n.
Exterior and interior angles
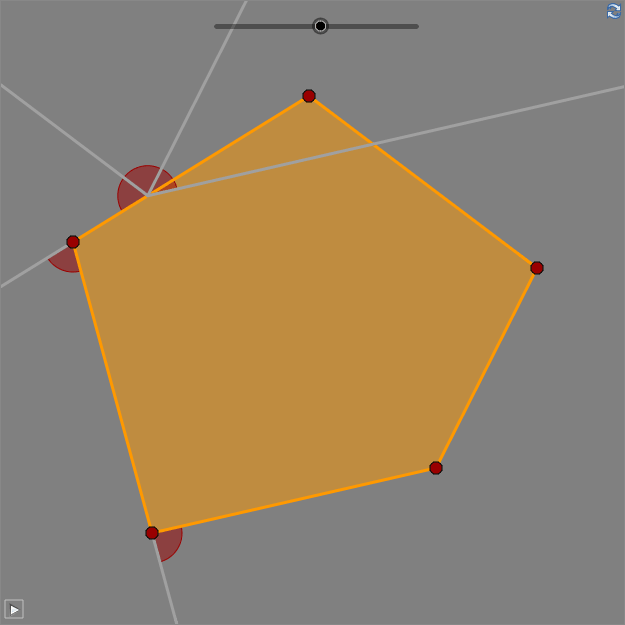
When doing the Scratch-tasks, the sprite turns an angle that is called an exterior angle to the polygon. For a regular polygon, the sum of the exterior angles is 360°. How do you know that the sum is always 360° from doing the Scratch-tasks?
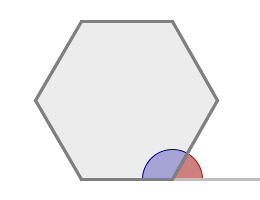
The sum of exterior angles of any polygon is always 360°, even if the polygon is not regular.
If all interior angles are less than or equal to 180° the polygon is a convex polygon. If an interior angle is greater than 180°, the corresponding exterior angle is considered to be negative. Negative exterior angles are shown as white in the worksheet above. The sum of the interior and exterior angle at a corner of a polygon, is always 180°.
Related angles
Often when doing geometry, the exact value in degrees is not interesting. Instead it is important to know how two angles relate to each other. Are they equal? Is one angle greater than or less than the other?
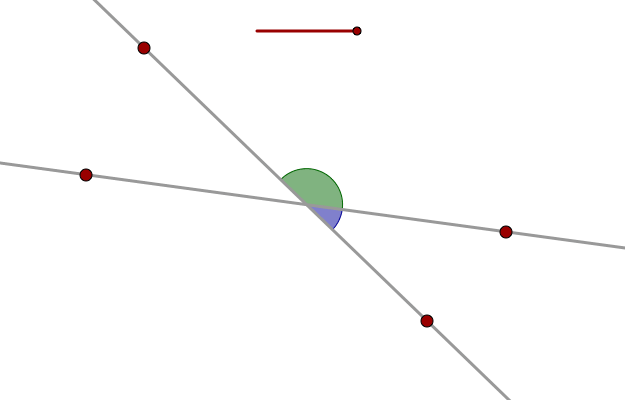
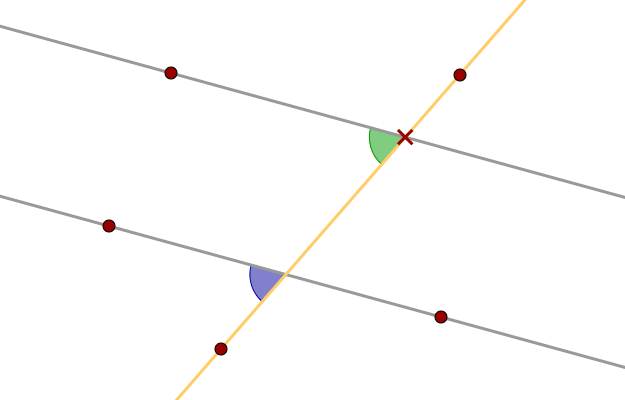
Vertical angles
Exercise 1 - Vertical angles
The red and the blue angle in the worksheet above are called vertical angles. Show that vertical angles always are equal (congruent). The worksheet above gives you a hint about how to show this relation.
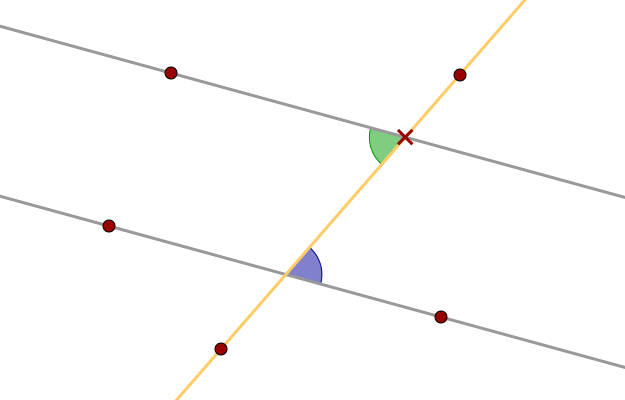
Corresponding angles
A line that crosses two other lines is called a transversal. In the worksheet above, the yellow line is a transversal. Drag the cross to move the green angle. Since the grey lines are parallel, the movement is a translation. The green and blue angles are therefore equal (congruent). This is always true for corresponding angles at parallel lines.
In the general case, the lines don't have to be parallel. If the angles are placed as in the worksheet above, they are still called corresponding angles, they are however not equal unless the lines are parallel. See Summary - Angles for more information.
Alternate angles
Exercise 2 - Alternate angles
The angles in the worksheet above are called alternate angles. Use the relations between vertical angles and corresponding angles at parallel lines, to show that alternate angles at parallel lines are always equal (congruent).
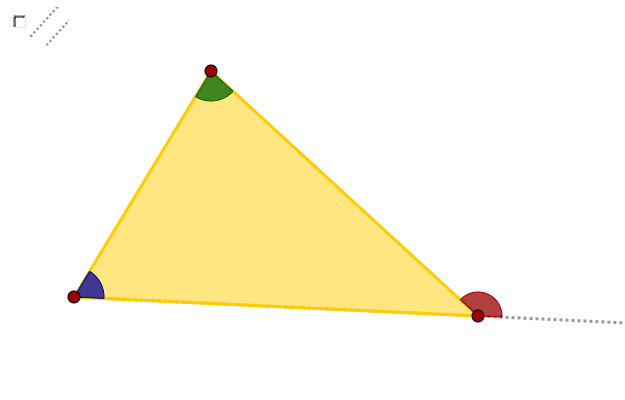
Exercise 3 - Angle sum of a triangle
Use angle relations and the construction below to show that the sum of the interior angles of a triangle is always 180°!
Angle sum of a triangle
Exercise 4 - The sum of the interior angles of various polygons
- If you have a quadrilateral you can always divide it into two triangles - show how! What is the sum of the interior angles of a quadrilateral?
- If you have a pentagon you can always divide it into three triangles - show how! What is the sum of the interior angles of a pentagon?
- What is the sum of the interior angles of a polygon with n vertices? Express your answer as an expression using n and explain why the expression holds.
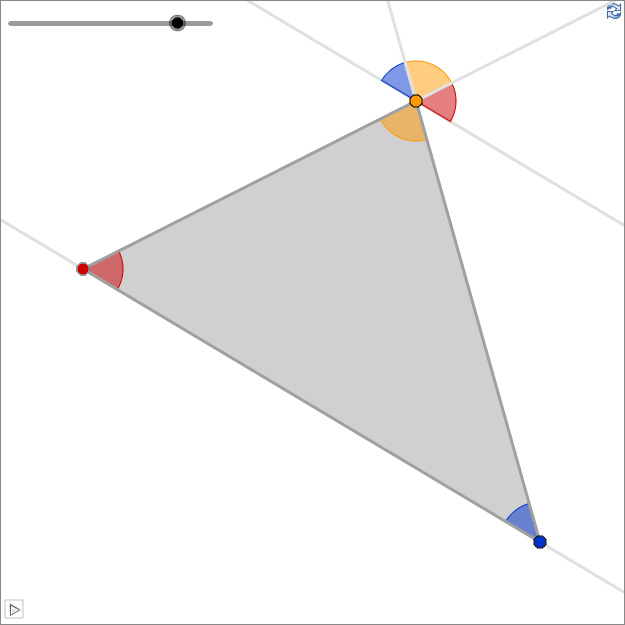
Exterior angle of a triangle
Exterior Angle Theorem
An exterior angle of a triangle equals the sum of the two opposite interior angles of the triangle.
In the worksheet above, the red angle is an exterior angle. The theorem states that the red angle is equal to the sum of the blue and green angle.
Exercise 5 - Exterior angle theorem
- Show the theorem by using the parallel line in the worksheet above, and by using related angles.
- Show the theorem by using the sum of the interior angles of a triangle.
further info:
Proof that the angles of a triangle sum to 360° from Uncyclopedia
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License