Derivatans definition

Derivatan i en punkt

Derivatan av en funktion \(f(x)\) i en punkt \( (a, f(a))\) skrivs som \(f'(a)\) och definieras som ett gränsvärde.

\[f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]

Värdet av

\[\frac{f(a+h)-f(a)}{h}\]

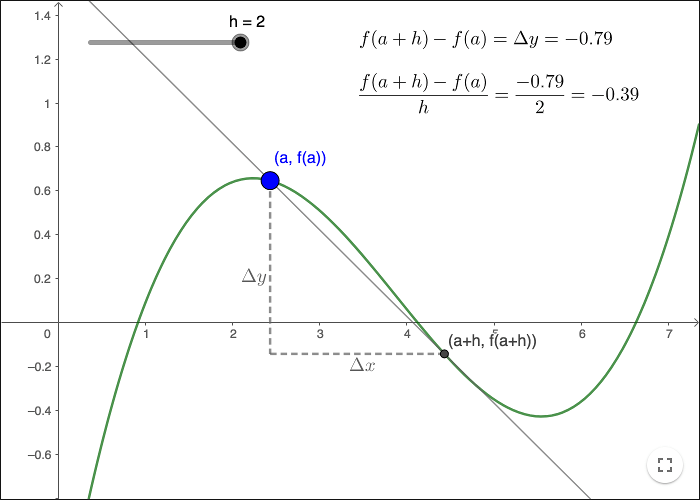
är lutningen till linjen genom punkterna \( (a, f(a))\) och \( (a+h, f(a+h))\), den så kallade sekantlinjen.

Observera att \(\Delta x = a+h-a=h\) och \(\Delta y = f(a+h)-f(a)\). Sekantlinjernas gränsvärde då \(h\) går mot noll är tangenten. Derivatan är tangentens lutning då tangenten går genom punkten där \(x=a\). Att bestämma derivatan kallas för att derivera.

Ladda GeoGebra-arbetsblad

Var på grafen är derivatan: positiv, negativ, noll? Spelar det någon roll om man närmar sig från höger eller vänster, om h är positiv eller negativ?

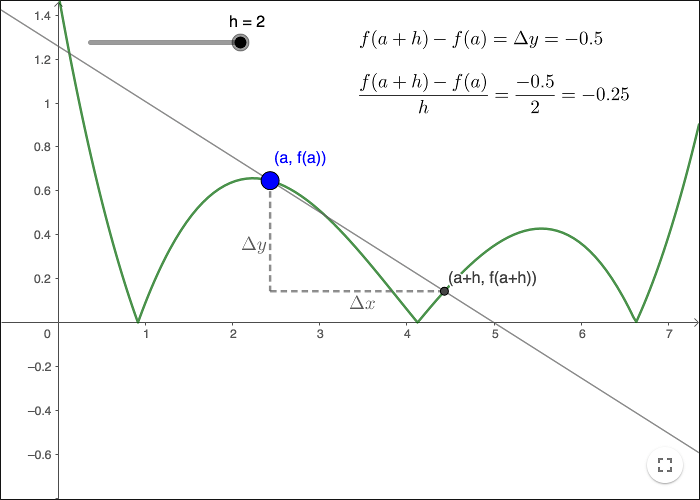
Om man tar absolutbeloppet av funktionen ovan får man grafen nedan.

Ladda GeoGebra-arbetsblad

I grafen ovan: finns det punkter som gör det svårt att definiera derivatan?

Derivatan som funktion

Man kan utvidga definitionen av derivatan i en punkt till att gälla alla punkter (alla punkter där derivatan är definierad, dvs där gränsvärdet existerar). En sådan utvidgning av definitionen innebär att man definierar en ny funktion som skrivs \(f'(x)\).

\[f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \]

Man kan i vissa fall bestämma en formel för derivatan genom att använda definitionen ovan. Sådana formler finns för alla standardfunktioner.

Om man använder en dator kan man numeriskt approximera derivatan i alla punkter till en graf.

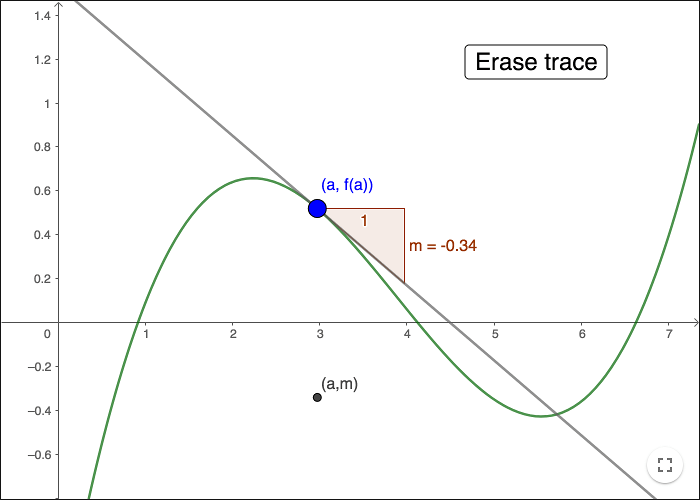
Linjen i konstruktionen nedan är tangenten till grafen i punkten A. Lutningen till tangenten är punkten Ps y-värde. Dra punkten A för att se spåret till P, detta spår är grafen till derivatans funktion.

Ladda GeoGebra-arbetsblad

Prova att ändra konstanttermen i funktionens definition så att grafen flyttas två enheter uppåt, dvs:

Lägg märke till att P ritar ut samma bana. Det finns oändligt många funktioner som har samma derivata. Dessa funktioner skiljer åt genom en konstant men deras grafer har alla "samma form".

Ett annat sätt att skriva det på

Om man istället använder \(y\) för att beteckna en funktion av variabeln \(x\), \(y=f(x)\). Så använder man beteckningen \(\frac{dy}{dx}\) för att beteckna derivatan. Beteckningen kommer från definitionen

\[\frac{dy}{dx}=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}\]

Derivatan av standardfunktioner

Man kan algebraiskt bestämma uttryck för derivatan av alla standardfunktioner. Innan vi gör detta ska vi undersöka standardfunktioner numeriskt.

Övning 1

Polynom

Ladda GeoGebra-arbetsblad

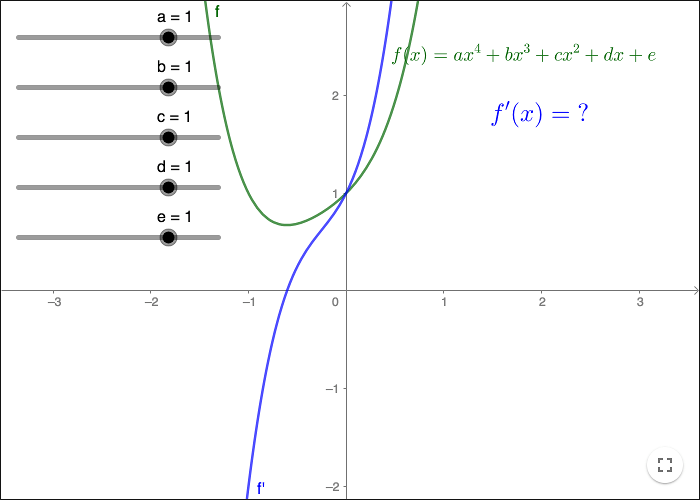
Gissa derivatans funktion!

• Den konstanta funktionen

  Låt \(a=b=c=d=0\). Bestäm en formel för \(f'(x)\)! Förklara!

• Polynom av första graden

  Låt \(a=b=c=0\), variera \(d\). Bestäm en exakt formel för \(f'(x)\)! Förklara!

  Vad händer med grafen till \(f'(x)\) då du ändrar på glidaren \(e\)? Förklara!

• Polynom av högre grad

  Vilken sorts funktion är \(f'(x)\) då \(f(x)\) är ett andragradspolynom?

  Vilken sorts funktion är \(f'(x)\) då \(f(x)\) är ett tredjegradspolynom? Gissa!

  Vilken sorts funktion är \(f'(x)\) då \(f(x)\) är ett fjärdegradspolynom? Gissa!

  Vad händer med grafen till \(f'(x)\) då du ändrar på glidaren \(e\)?

• Derivatan till ett polynom av grad \(n\)

  Försök att bestämma en exakt formel för \(f'(x)\) då \(f(x)=cx^2\) (låt glidarna \(a, b, d, e\) vara 0). Hur beror linjens lutning på talet \(c\)? Testa genom att pröva olika värden på glidaren c.

  Om du känner till formeln för \(f'(x)\) då \(f(x)=ax^0, f(x)=ax^1, f(x)=ax^2\); kan du då gissa formeln för \(f'(x)\) då \(f(x)=ax^3\) och \(f(x)=ax^4\).

• Omvänd derivering

  Om \(f'(x)=3\) vad är då \(f(x)\)? Kan olika funktioner ha samma derivata?

  Om \(f'(x)=4x\) vad är då \(f(x)\)?

  Om \(f'(x)=6x^2\) vad är då \(f(x)\)?

  Om \(f'(x)=x^{-1}\) vad är då \(f(x)\)?

Övning 2

Sinus och cosinus

Ladda GeoGebra-arbetsblad

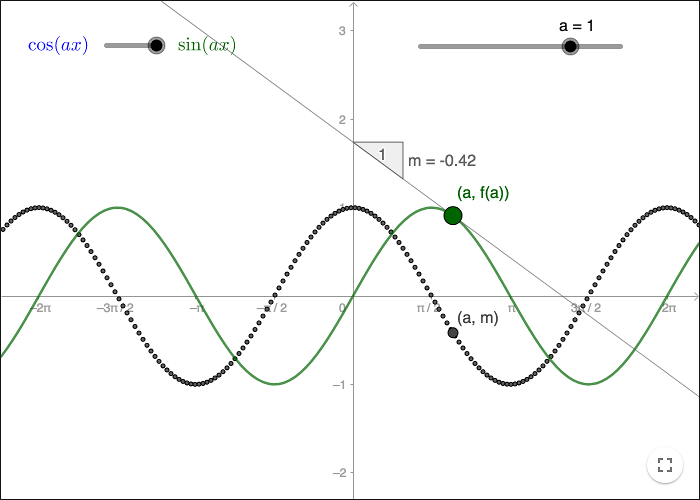
Gissa derivatans funktion till funktionen \(f(x)=\sin (ax)\) då \(a=1\).

Gissa derivatans funktion till funktionen \(f(x)=\sin (ax)\) då \(a\neq 1\).

Byt till funktionen \(f(x)=\cos (ax)\) genom att ändra den vänstra glidaren. Gissa derivatans funktion till funktionen \(f(x)=\cos (ax)\) då \(a=1\).

Gissa derivatans funktion till funktionen \(f(x)=\cos (ax)\) då \(a\neq 1\).

Övning 3

Exponentialfunktionen - gissa basen

Ladda GeoGebra-arbetsblad

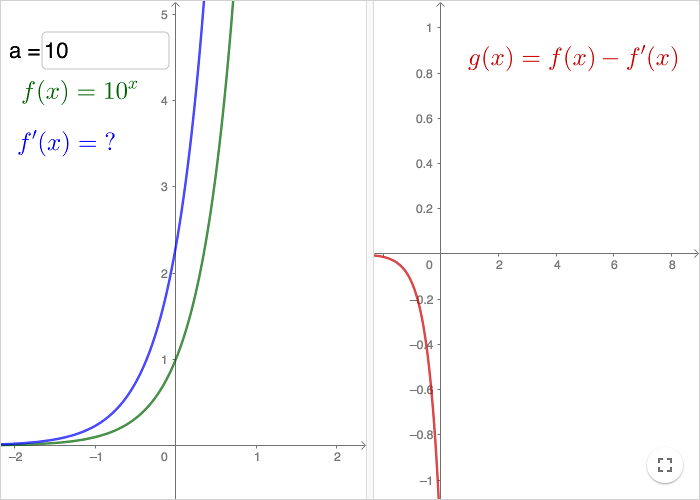
Till vänster i arbetsbladet ovan visas funktionen \(f(x)=a^x\) och dess derivata. Till höger visas skillnaden mellan dessa två funktioner.

Ändra exponentialfunktionens bas genom att skriva in ett nytt värde för \(a\) i inmatningsrutan.

Hitta ett värde på basen som minimerar skillnaden mellan de två funktionerna, värdet skall vara korrekt till fyra gällande siffror.

Övning 4

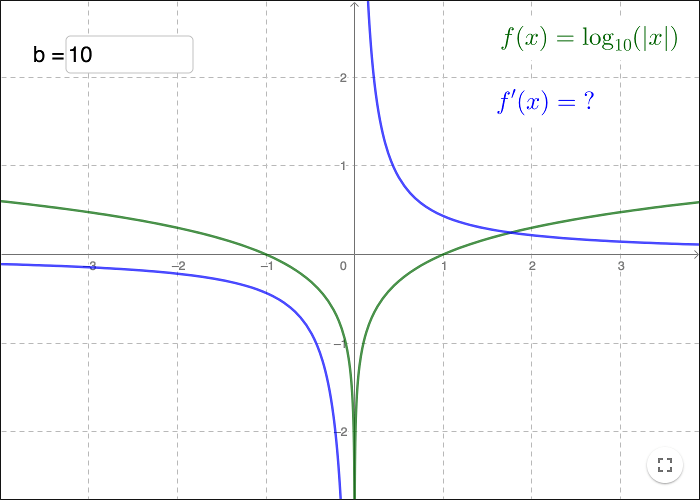
Logaritmfunktionen med en lämplig bas

Ladda GeoGebra-arbetsblad

Försök hitta en bas \(b\) så att derivatan blir \(\frac{1}{x}\).