Fixpunkter och spindelvävsdiagram
En generell rekursiv ekvation kan skrivas så här
\[ \left\{ \begin{align*} a_0 &= c \\ a_{n+1} &= f(a_n),n\geq0 \end{align*} \right. \]
Om \(a_n\) har ett gränsvärde då \(n\rightarrow \infty\) , och om man applicerar funktionen \(f\) på detta gränsvärde så kommer resultatet att bli samma tal igen. Gränsvärdet kallas fixpunkt. Om vi kallar fixpunkten för \(x_0\), så är denna likhet sann:
\[f(x_0)=x_0\]
Man bestämmer fixpunkter till en rekursiv ekvation genom att lösa ekvationen \(f(x)=x\).
Då man itererar den rekursiva ekvationen applicerar man samma funktion på sig själv om och om igen.
\[x,f(x),f(f(x)),f(f(f(x))),\ldots \]
Om den rekursiva ekvationen är
\[ \left\{ \begin{align*} a_0 &= c \\ a_{n+1} &= 1+\frac{1}{a_n},n\geq0 \end{align*} \right. \]så blir funktionen av funktionen av..., ett kedjebråk
\[1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}\]Om den rekursiva ekvationen är
\[ \left\{ \begin{align*} a_0 &= c \\ a_{n+1} &= \sqrt{1+a_n},n\geq0 \end{align*} \right. \]så blir funktionen av funktionen av..., ett kedjerotuttryck
\[\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}\]Attraherande eller repellerande fixpunkter
En fixpunkt kan vara attraherande eller repellerande.
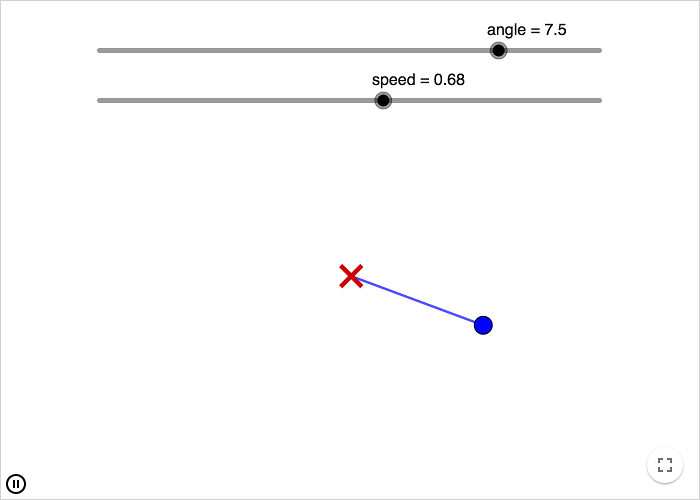
Dämpad pendel
En dämpad pendel har två fixpunkter. Den ena är när pendeln pekar nedåt med vinkeln 0; den andra är när pendeln pekar uppåt med vinkeln π. I teorin (om man bortser från Heisenbergs osäkerhetsrelation) kommer en pendel som har vinkeln π som utgångsläge att förbli vid denna vinkel, detta är en repellerande fixpunkt. Om pendeln rör sig aldrig så lite åt något håll, kommer den emellertid så småningom att hamna vid vinkeln 0, som är en attraherande fixpunkt.
Repellerande fixpunkter
Om fixpunkterna är irrationella tal kommer du aldrig att hitta dem genom att iterera en rekursiv ekvation. Även om du startar med den repellerande fixpunkten kommer värdena att avlägsna sig från denna då du itererar. Oavsett hur många korrekta decimaler en elektronisk apparat kan räkna med, kan den ändå aldrig räkna med oändligt många korrekta decimaler; det kommer alltid att finnas en avvikelse från det exakta värdet. För att hitta repellerande fixpunkter krävs det en annan metod.
För en rekursiv ekvation
\[ \left\{ \begin{align*} a_0 &= c \\ a_{n+1} &= f(a_n),n\geq0 \end{align*} \right. \]
kan du lösa ekvationen
\[f(x)=x\]
Fixpunkterna är skärningspunkterna mellan linjen och funktionens graf.
Du kan använda en bild för att göra ett spindelvävsdiagram Ett spindelvävsdiagram visar huruvida en fixpunkt är repellerande eller attraherande.
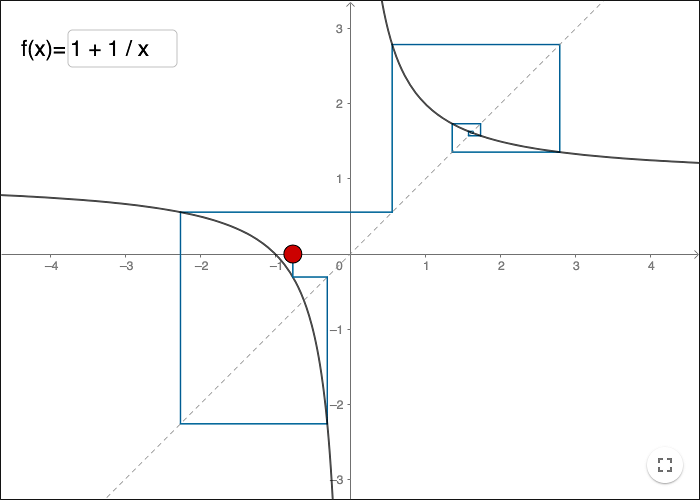
Spindelvävsdiagram
Iterationer av den rekursiva ekvationen
\[ \left\{ \begin{align*} a_0 &= c \\ a_{n+1} &= 1+\frac{1}{a_n},n\geq0 \end{align*} \right. \]
kan illustreras grafiskt med så kallade spindelvävsdiagram.
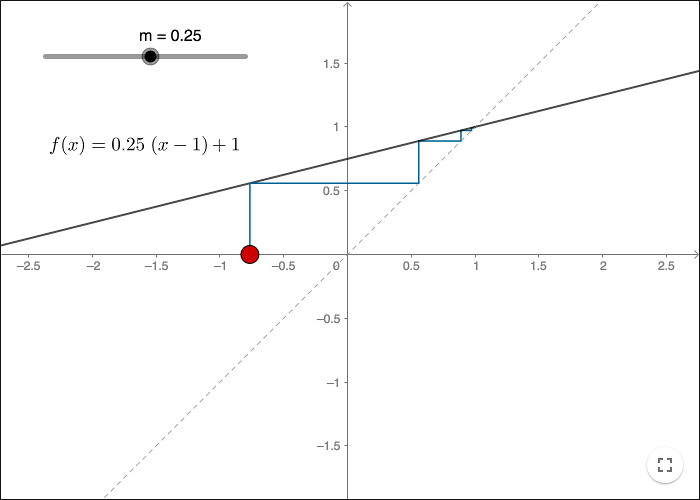
Funktionens lutning
En punkt som är "tillräckligt nära" en attraherande fixpunkt kommer att närma sig fixpunkten då den itereras. Funktionens lutning vid fixpunkten avgör huruvida fixpunkten är attraherande eller repellerande (eller varken det ena eller det andra),
Om du kan klassifisera en fixpunkt till en linjär funktion efter funktionens lutning, då kan du klassisera en fixpunkt till vilken deriverbar funktion som helst efter funktionens derivata i fixpunkten.
Övningar
Övning 1
Fixpunkter
Bestäm fixpunkterna till kedjebråket
\[1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}\]Bestäm fixpunkterna till kedjerotuttrycket
\[\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}\]
Övning 2
Gör ett spindelvävsdiagram i GeoGebra
- Lägg in en funktion \(f(x) = 1+1/x\), en linje \(y = x\) och en punkt \(A\) på \(x\)-axeln.
- Använd verktygen
Vinkelrät linje och skärningspunkter för att markera punkter i spindelvävsdiagrammet. Zooma in när du närmar dig fixpunkten. Låt diagrammet börja i punkten \(A\).
- Dölj alla linjer och lägg in sträckor mellan punkterna. Dölj alla punker utom \(A\).
- Välj verktyget
Inmatningsfält och länka fältet till funktionen \(f(x)\).
Övning 3
Gör ett spindelvävsdiagram med hjälp av kalkylbladet
- Lägg in en funktion \(f(x) = 1+1/x\), en linje \(y = x\) och en punkt \(A\) på \(x\)-axeln.
- Välj
Visa -> Kalkylbladi menyn.- Lägg in
x(A)i cell A1 - Lägg in
f(A1)i cell B1 - Lägg in
(A1, B1)i cell C1 - Lägg in
(B1, B1)i cell D1 - Lägg in
x(D1)i cell A2
- Lägg in
- För att visa sträckorna:
- Lägg in
Sträcka(C1, D1)i cell E1 - Lägg in
Sträcka(C2, D1)i cell F2
- Lägg in
- Gör relativa kopior.
- Välj verktyget
Inmatningsfält och länka fältet till funktionen \(f(x)\).
Övning 4
Repellerande och attraherande fixpunkter
Använd en GeoGebra-fil som visar ett spindelvävsdiagram. Lägg in en glidare k och testa spindelvävsdiagrammet på funktionen:
\[f(x) = 1+k x\]För vilka lutningar är fixpunkten attraherande/repellerande?
Övning 5
Logistisk avbildning
Använd en GeoGebra-fil som visar ett spindelvävsdiagram. Lägg in en glidare r och testa spindelvävsdiagrammet på funktionen
\[f(x) = r x\cdot (1-x)\]där \(0\le r \le 4\). Försök hitta värden på r som åskådliggör:
- konvergens mot \(0\).
- konvergens mot en fixpunkt \(\ne 0\).
- hopp mellan två olika värden.
- hopp mellan fyra olika värden.
- ett till synes kaotiskt uppförande.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License