Integraler
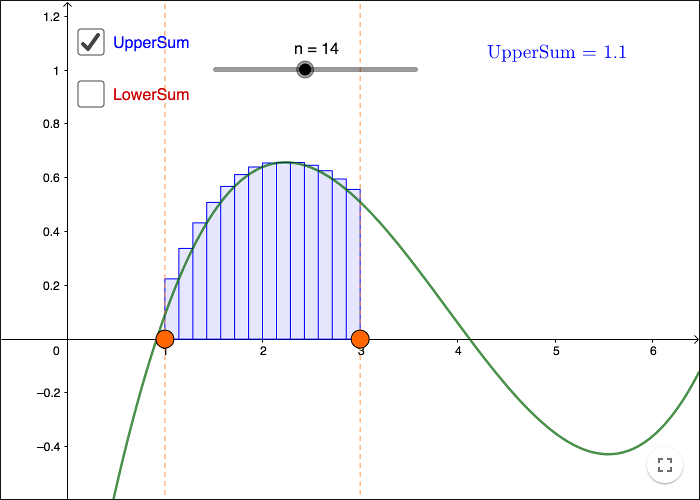
Ett sätt att approximera arean under en graph är att approximera arean med ett antal rektanglar. Ett antal rektanglar som approximerar arean under en graf kallas för en trappstegsfunktion.
Det finns två olika standardsätt att skapa rektanglarna på. Med GeoGebra kan du använda två kommandon. Låt \(f\) vara en funktion, \(a\) det första \(x\)- värdet och \(b\) det andra, låt \(n\) vara antalet rektanglar, då kan du skriva
Översumma( f , a, b, n )
eller
Undersumma( f , a, b, n )
Funktionen måste vara definierad på intervallet \([a, b]\).
På engelska heter dessa kommandon UpperSum och LowerSum. Du kan se skillnaden mellan kommandona i arbetsbladet nedan.
Lägg märke till att om du försöker approximera arean mellan \(x = 5\) och \(x = 6\), får du negativa värden. Eftersom en area inte kan vara negativ, är det inte arean du får av en trappstegsfunktion. Du får antingen arean eller det negativa värdet av arean, beroende på om grafen ligger ovanför eller under \(x\)-axeln.
För att hantera areor under grafer algebraiskt, används så kallade integraler. Integraler kan definieras med hjälp av trappstegsfunktioner, som gränsvärdet då antalet rektanglar går mot oändligheten.
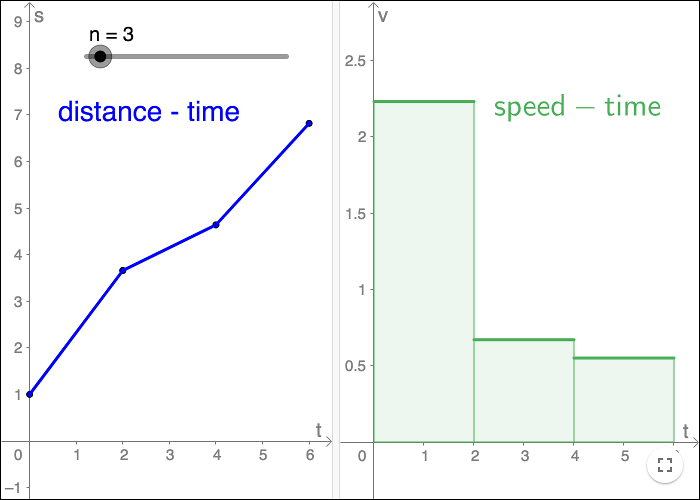
Så varför skulle man då vilja beräkna arean under en graf? Ett konkret exempel har att göra med sträcka och fart. Om du känner till ett föremåls fart, kan du beräkna hur lång sträcka föremålet färdats, genom att beräkna ‐ arean under en graf.
Sträcka och fart
Om ett föremål förflyttar sig med en konstant fart under ett tidsintervall \(\Delta t\), så gäller följande samband för den sträcka föremålet förflyttat sig, \(\Delta s\), och farten \(v\):
\[v=\frac{\Delta s}{\Delta t} \hspace{0.5 cm} \text{och} \hspace{0.5 cm} \Delta s = v\cdot \Delta t\]Grafiskt får man farten genom att ta lutningen av linjesegmentet i s-t-diagrammet, funktionen \(s(t)\). Den totala sträcka föremålet förflyttat sig, kan man beräkna antingen genom att använda funktionen \(s(t)\) eller funktionen \(v(t) \).
Om funktionen \(s(t) \) inte är en linjär funktion (om farten inte är konstant) då kan man approximera \(s(t)\) med en funktion som är linjär på mindre tidsintervall och sedan använda samma resonemang. Ju finare indelning som används, desto bättre är approximationen.
Om man delar in tiden i kortare tidsintervall, och antar att föremålet håller en konstant fart inom varje sådant intervall; då får man fram farten genom att betrakta lutningen i ett givet intervall i s-t-diagrammet.
För att beräkna den sammanlagda sträckan kan man addera rektangelareor, detta ger en approximation av den sammanlagda sträckan.
Om man låter antalet intervall gå mot oändligheten så gäller att det att \(\Delta t \rightarrow 0\). Man kan nu bestämma hastigheten vid en given tidpunkt genom att derivera.
\[v=\frac{ds}{dt}\]
När \(\Delta t \rightarrow 0\), går arean under grafen till \(v(t)\) mot den sammanlagda sträckan, dvs \(s(b)-s(a)\).
Om vi nu känner till funktionen \(v(t)\), men inte funktionen \(s(t)\), då kan vi beräkna arean under grafen genom att först ta reda på någon funktion som har \(v(t)\) som sin derivata. Vi gör omvändningen till att derivera.
Primitiva funktioner
Den primitiva funktionen till en funktion \(f(x)\), är en funktion \(F(x)\) sådan att \(F'(x) = f(x)\).
Det finns oändligt många primitiva funktioner till en funktion \(f\). Funktionerna
\[ \begin{align} F_1(x) &= \frac{x^2}{2}+5 \\ F_2(x) &= \frac{x^2}{2} \\ F_3(x) &= \frac{x^2}{2}-300 \end{align} \]är alla primitiva funktioner till \(f(x)=x\).
Om du ska bestämma en primitiv funktion, kan du lägga till en konstant \(C\) för att på så vis få med alla primitiva funktioner. Funktionen
\[F(x) = \frac{x^2}{2}+C, \]där \(C\) är en konstant, är primitiv funktion till \(f(x) = x\).
Från trappstegsfunktion till integral
Arean av trappstegsfunktionen ovan är
\[A=f(x_0)\cdot \Delta x + f(x_1)\cdot \Delta x + f(x_2)\cdot \Delta x + f(x_3)\cdot \Delta x + f(x_4)\cdot \Delta x \]Låt \(F(x)\) vara en primitiv funktion till \(f(x)\), dvs en funktion sådan att \(F'(x)=f(x)\). Om \(\Delta x\) är "litet", kan vi göra följande approximation
\[f(x_i)\approx \frac{F(x_{i+1})-F(x_i)}{\Delta x} \text{ for } i=0,1,2,3,4\]Detta ger oss följande approximation för arean
\[A\approx \frac{F(x_1)-F(x_0)}{\Delta x}\cdot \Delta x + \frac{F(x_2)-F(x_1)}{\Delta x}\cdot \Delta x + \frac{F(x_3)-F(x_2)}{\Delta x}\cdot \Delta x \\ + \frac{F(x_4)-F(x_3)}{\Delta x}\cdot \Delta x + \frac{F(x_5)-F(x_4)}{\Delta x}\cdot \Delta x \]Förkorta bort alla \(\Delta x\)
\[ \begin{align} A &\approx F(x_1)-F(x_0) + F(x_2)-F(x_1) + F(x_3)-F(x_2) + F(x_4)-F(x_3) + F(x_5)-F(x_4)\\ &=F(x_5)-F(x_0) \end{align} \]Låt antalet intervall gå mot oändligheten, då gäller att \(\Delta x \rightarrow 0\). Om intervallets ändpunkter heter \(a\) och \(b\), får vi att
\[A=F(b)-F(a)\]Arean \(A\) är alltså ett gränsvärde av en summa av termer på formen
\[f(x_i)\Delta x.\]Vi skriver \(A\) med hjälp av ett integraltecken, vilket ser ut som en S-formad variant av det sigma-tecken ( \(\sum\) ) som används för summa. Intervallets ändpunkter skrivs nedanför och ovanför integraltecknet.
\[A = \int_a^b\! f(x) \,dx \]Ibland används integraltecknet utan intervall-ändpunkter för att beteckna en primitiv funktion.
\[\int\! f(x) \,dx = F(x) \]Analysens huvudsats
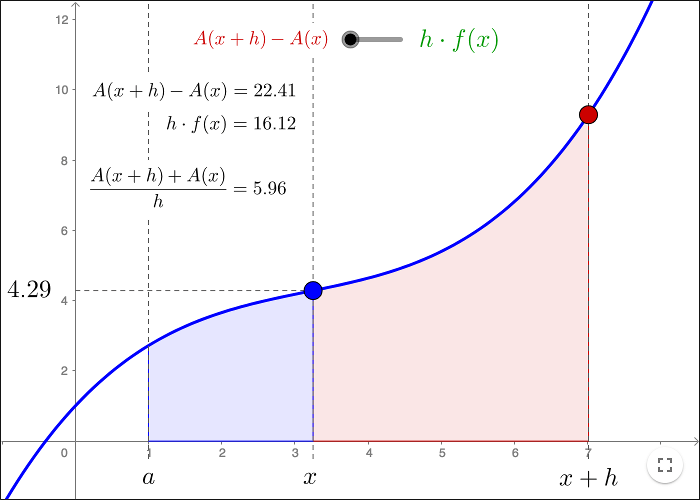
Låt \(f(x)\) vara en kontinuerlig funktion på intervallet \([a, b]\). Vi kan definiera en funktion \(A(x)\) som aren under grafen till \(f\) på intervallet \([a,x]\).
Enligt analysens huvudsats är
\[A'(x) = f(x)\]för alla \(x\in [a, b] \).
För att visa satsen måste vi visa att
\[\lim_{h\rightarrow 0}\frac{A(x+h)-A(x)}{h}=f(x)\]
Resonemanget visas översiktligt i arbetsbladet nedan.
Eftersom alla primitiva funktioner till en given funktion bara skiljer sig med åt med en konstant, kan man använda vilken primitiv funktion som helst för att beräkna arean under \(f(x)\) i ett intervall \([a,b]\). Låt \(F(x)\) vara en primitiv funktion till \(f(x)\), då är \(F(x)=A(x)+C\) för någon konstant C. Då är
\[\int_a^b \! f(x) \, dx = F(b)-F(a)=A(b)+C-(A(a)+C)=A(b)-A(a)=A(b)-0=A(b)\]Om alltså \(F(x)\) är en primitiv funktion till \(f(x)\), så är \[ \frac{d}{dx} \int_a^x\! F(x)\, dx = f(x).\]
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License