Trigonometric Identities
Identity and equation
The difference between these two equalities \(x(x-1)=0\) and \(x(x-1)=x^2-x\), is that the first one is true for some values of \(x\), and the second is true for all \(x\). An equality that is true for all values is an identity. In some books the symbol \(\equiv \) is used to denote identities, as in \(x(x-1)\equiv x^2-x\).
Identities from the unit circle
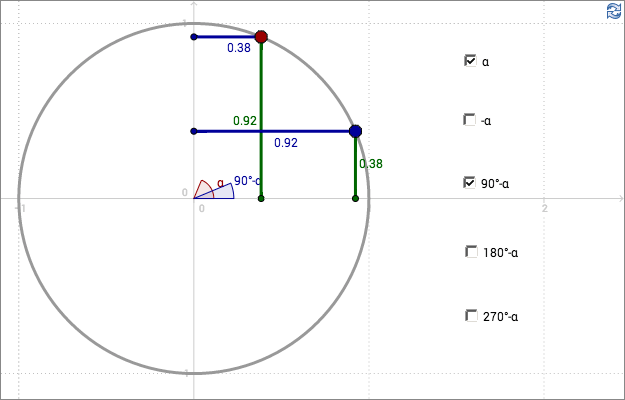
Which of following identities are true?
| \(\sin \alpha = \sin (-\alpha)\) | \(\sin \alpha = \cos (90^\circ -\alpha)\) | \(\sin \alpha = \sin (180^\circ -\alpha)\) | \(\sin \alpha = \cos (270^\circ -\alpha)\) |
| \(\sin \alpha = -\sin (-\alpha)\) | \(\cos \alpha = \sin (90^\circ -\alpha)\) | \(\sin \alpha = -\sin (180^\circ -\alpha)\) | \(\cos \alpha = \sin (270^\circ -\alpha)\) |
| \(\cos \alpha = \cos (-\alpha)\) | \(\sin \alpha = -\cos (90^\circ -\alpha)\) | \(\cos \alpha = \cos (180^\circ -\alpha)\) | \(\sin \alpha = -\cos (270^\circ -\alpha)\) |
| \(\cos \alpha = -\cos (-\alpha)\) | \(\cos \alpha = -\sin (90^\circ -\alpha)\) | \(\cos \alpha = -\cos (180^\circ -\alpha)\) | \(\cos \alpha = -\sin (270^\circ -\alpha)\) |
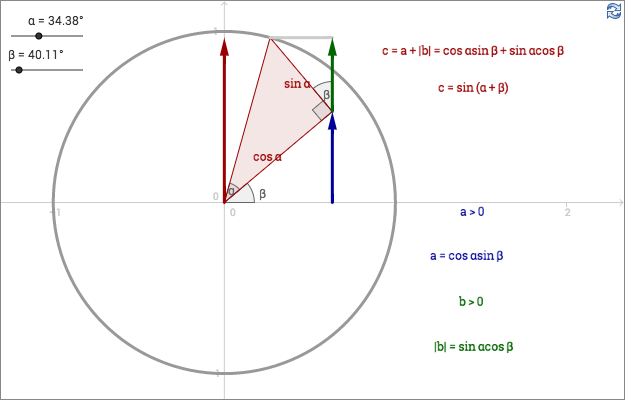
Addition formula for sine
In the applet above, an angle in each quadrant is deduced from the explanation below.
Furthermore, following identities are used:
\[\sin(\beta -90^\circ)=-\sin(90^\circ -\beta)=-\cos \beta \]
\[\cos(\beta-180^\circ)=\cos(180^\circ-\beta)=-\cos\beta \]
\[\sin(\beta -270^\circ)=-\sin(270^\circ -\beta)=\cos \beta \]
In this demonstration, \(\alpha\) is restricted to \(0^\circ \lt \alpha \lt 90^\circ \) since it is an angle in a right-angled triangle. There is no restriction on \(\beta \), it can be in any quadrant. The restriction seen in the applet, \(0 \le \beta \lt 360^\circ \), stems from the fact that GeoGebra can only show those angles.
Using the identities \(\sin(-\beta)=-\sin(\beta)\) and \(\cos(-\beta)=\cos(\beta)\) we get that:
\[\sin(\alpha-\beta)=\sin(\alpha + (-\beta))=\sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta)=\sin \alpha \cos \beta - \cos \alpha \sin \beta\]
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta + \cos \alpha \sin \beta\]
\[\sin(\alpha-\beta)=\sin \alpha \cos \beta - \cos \alpha \sin \beta\]
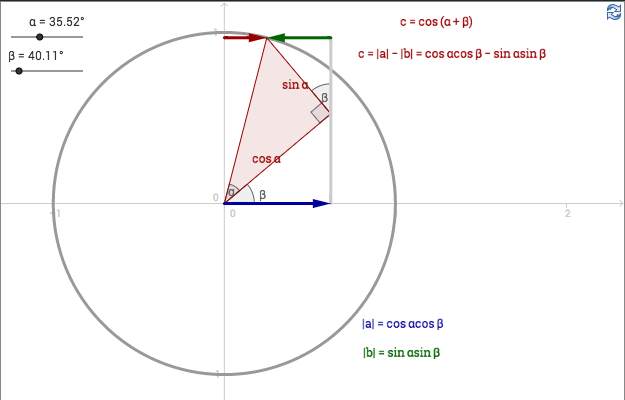
Addition formula for cosine
Apart from the identities that are used for explaining the addition formula for sine, following identities are also used in the applet above:
\[\cos(\beta -90^\circ)=\cos(90^\circ -\beta)=\sin \beta \]
\[\sin(\beta-180^\circ)=-\sin(180^\circ-\beta)=-\sin\beta \]
\[\cos(\beta -270^\circ)=\cos(270^\circ -\beta)=-\sin \beta \]
Using the identities \(\sin(-\beta)=-\sin(\beta)\) and \(\cos(-\beta)=\cos(\beta)\) we get that:
\[\cos(\alpha-\beta)=\cos(\alpha + (-\beta))=\cos \alpha \cos (-\beta) - \sin \alpha \sin (-\beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta\]
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta\]
\[\cos(\alpha-\beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta\]
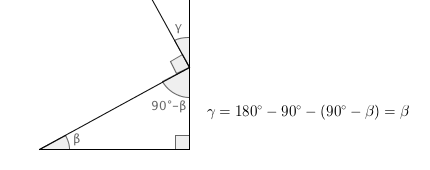
When both angles are larger than 90°
The addition formulas are true even when both angles are larger than \(90^\circ\). Assume that \(90^\circ\lt \alpha \lt 180^\circ\). Let \(\alpha ' =\alpha -90^\circ\). From the symmetry of the unit circle we get that \(\sin \alpha =\sin(90^\circ +\alpha ')=-\cos \alpha '\) and \(\cos \alpha=\cos(90^\circ+\alpha ')=-\sin\alpha '\). Using these identities we get:
\[\sin(\alpha + \beta)=\sin(90^\circ + \alpha ' + \beta)=-\cos(\alpha ' +\beta )\]
We can now use the addition formula since \(\alpha ' \lt 90^\circ \).
\[-\cos(\alpha ' +\beta )=-\cos \alpha ' \cos \beta +\sin \alpha ' \sin\beta = \sin\alpha\cos\beta+\sin\beta\cos\alpha\]
In a similar way we can prove that all addition formulas are true for all angles.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License