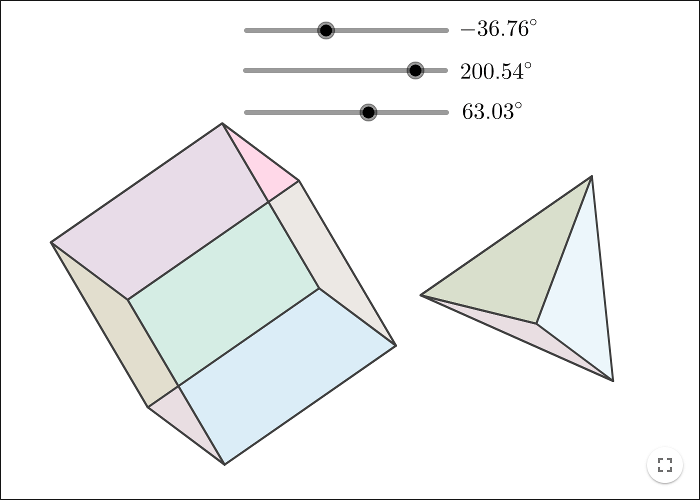
Rotera en kub

Ladda GeoGebra-arbetsblad

Projicera 3D på 2D

En punkt i ett tredimensionellt koordinatsystem kan representeras av en \(3\times 1\) matris. Då man modellerar tre dimensioner på en tvådimensionell datorskärm, måste man projicera varje punkt till 2D. Efter projiceringen, skall varje punkt representeras av en \(2\times 1\) matris.

Om man antar att \(z\)-axeln (eller den tredje basvektorn) pekar ut från datorskärmen, så är skärmen en projicering på \(xy\)-planet.

Projektionsmatrisen \(\mathbf{P}\) måste avbilda matrisen \(\mathbf{v}=\left( \begin{array}{} a\\b\\c\\ \end{array}\right)\) på en matris \(\mathbf{w}=\left( \begin{array}{} a\\b\\ \end{array}\right)\). Detta kan man åstadkomma genom att låta

\[\mathbf{P}=\left( \begin{array}{} 1 & 0 & 0\\0 & 1 & 0\\ \end{array}\right)\]

Sedan låter man \(\mathbf{w}=\mathbf{P}\mathbf{v}\).

Matris som en visuell punkt

I GeoGebra representeras matriser av listor. En \(2\times 1\) matris syns inte i ritområdet.

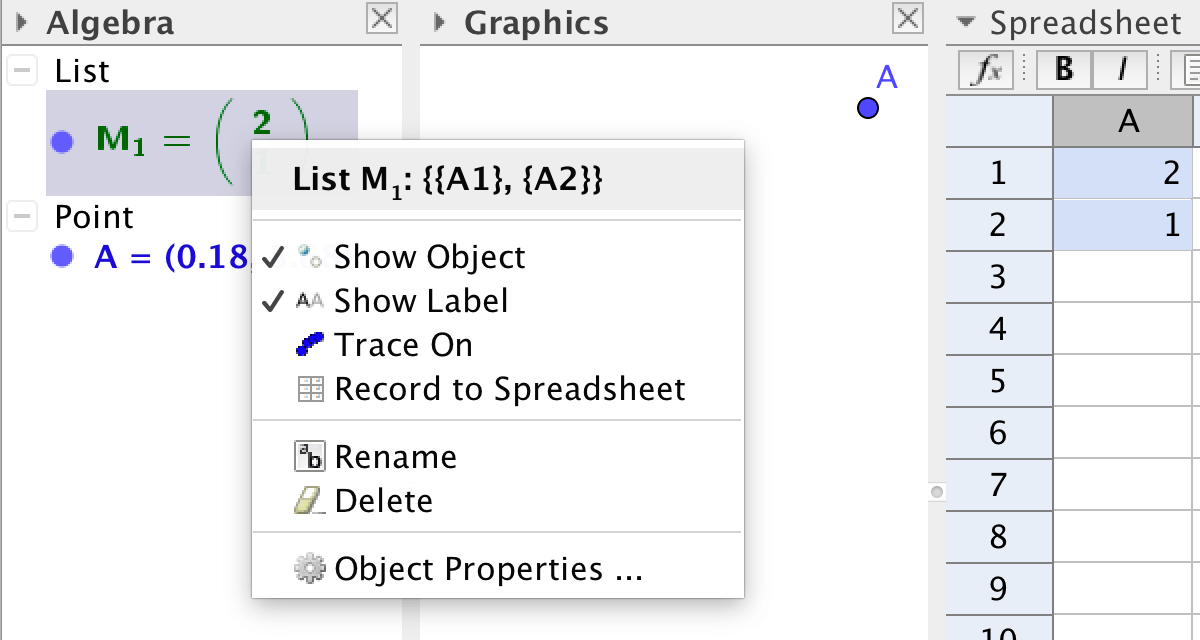
Om man vill visa en matris \(\mathbf{matrix1}=\binom{2}{1}\) som en punkt, måste man använda matriselementen som koordinater till en ny punkt. Man kommer åt ett matriselement med kommandot Element[<matris>, <rad>, <kolumn>].

För att visa en \(2\times 1\)-matrix \(\mathbf{w}\) som en punkt \(A\), skriver man:

A=(Element[w,1,1],Element[w,2,1])

Övning 1

• Gör tre glidare för att representera matriselementen \(v_x, v_y, v_z\) till en matris \(\mathbf{v}\).

• Skapa matrisen \(\mathbf{v}\) genom att använda kalkylbladet eller genom att skriva den som en lista i inmatningsraden: v={{v_x},{v_y},{v_z}}

• Skapa projektionsmatrisen \(\mathbf{P}\).

• Skapa den projicerade matrisen \(\mathbf{w}=\mathbf{P}\mathbf{v}\) genom att skriva i inmatningsraden: w=P v

• Skapa en punkt A som har matriselementen till \(\mathbf{w}\) som koordinater.

• Ändra på glidarna. Då man ändrar glidaren \(v_z\), skall ingenting hända med punkten \(A\).

Rotationerna

Om z-axeln pekar ut från skärmen, och om man roterar basvektorerna med vinkeln \(\alpha\) runt z-axeln, får man de roterade vektorerna som i bilden nedan.

Den tredje basvektorn, den som är parallell med z-axeln, påverkas inte.

Rotationsmatrisen \(\mathbf{T_z}\) för rotation runt z-axeln blir:

\[\mathbf{T_z}=\left( \begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array} \right) \]

På liknande vis finner man rotationsmatriserna runt x- respektive y-axeln.

\[\mathbf{T_x}=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array} \right) \]

\[\mathbf{T_z}=\left( \begin{array}{ccc} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{array} \right) \]

Övning 2

• Lägg in tre glidare för att representera vinklarna, en vinkel per axel/basvektor.

• Skriv in de tre rotationsmatriserna, en matris till varje vinkel.

• Istället för att bara projicera matrisen \(\mathbf{v}\) till 2D, måste den nu roteras innan den projiceras. Ändra definitionen av matrisen \(\mathbf{w}\) från \(\mathbf{w}=\mathbf{Pv}\) till \(\mathbf{w}=\mathbf{PT_xT_yT_zv}\)

Kubens hörn

På samma sätt som matrisen v transformeras, skall nu kubens åtta hörn roteras, projiceras och sedan representeras av visuella punkter. Eftersom det är samma operationer som skall utföras åtta gånger, är det enklast att använda kalkylbladet.

Låt kuben ha sina hörn i koordinaterna (1,1,1), (1,-1,1), (-1,1,1), (-1,-1,1), (1,1,-1), (1,-1,-1), (-1,1,-1) och (-1,-1,-1).

Ett sätt att utföra operationerna på, är att lägga in koordinaterna i kalkylbladet och sedan:

• Skapa en matris av koordinaterna till ett hörn, gör sedan relativa kopior av denna matris.

• Utför transformationerna på en matris, gör sedan relativa kopior av resultatet.

• Skapa en punkt av en resultatmatris, gör sedan relativa kopior av punkten.

Operationerna görs i kolumn A i bilden nedan. De relativa kopiorna görs sedan åt höger.

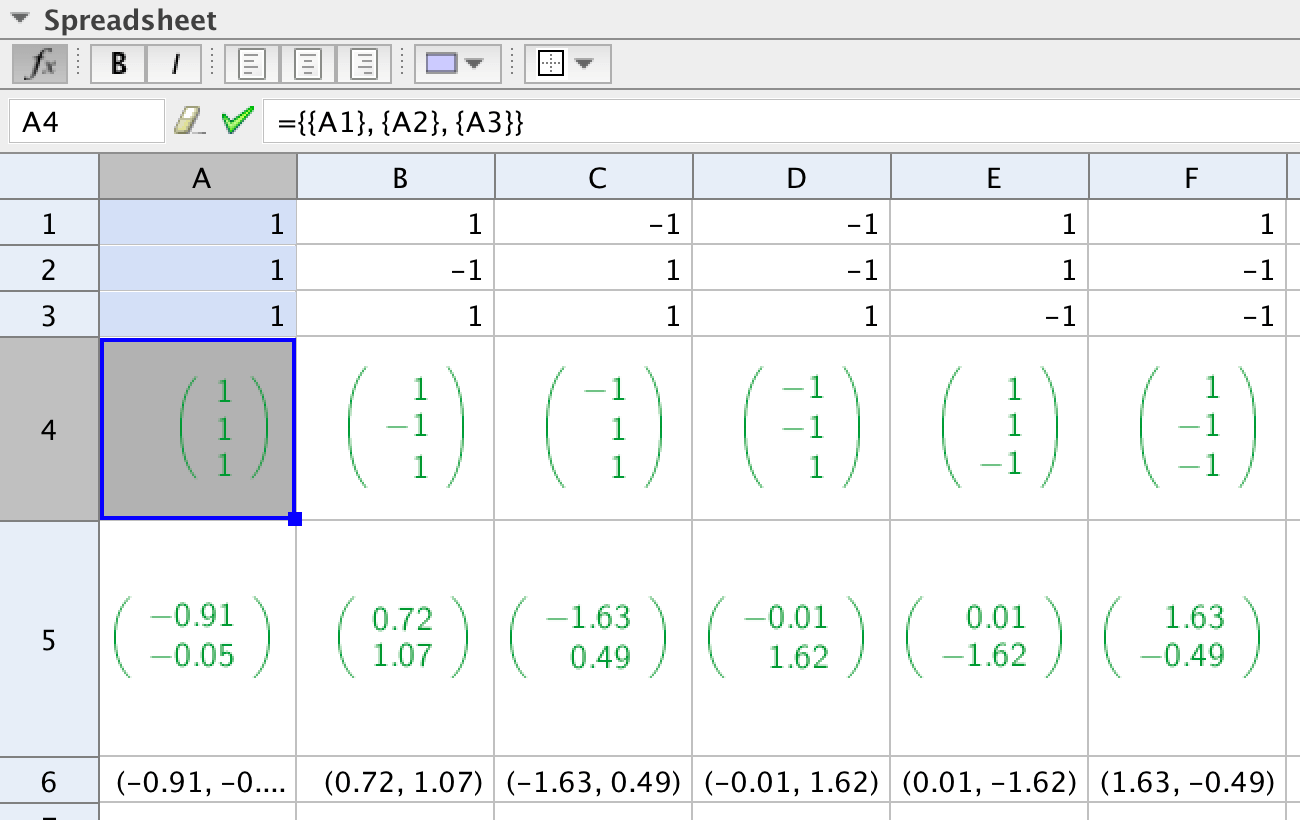
Rotera runt punkterna och fyll i kubens sidor genom att använda Polygon-verktyget.

Man kan givetvis tänka sig andra placeringar av kubens hörn.

Med hjälp av detta kalkylblad kan man nu rotera valfria 3D object och projicera dem på 2D.