Make Fractals of Images
Select an image and then generate a Julia set or a Mandelbrot set.

Select an image and then generate a Julia set or a Mandelbrot set.

Generate Julia sets and the Mandelbrot set using four different, and adjustable, orbit traps.

Interactive Julia set, animation bewteen two Julia sets, and basic information about Julia sets.

Interactive Möbius transformation of a Doyle Spiral.

Interactive examples of rolling hypocycloids, epicycloids and similar shapes.

Interactive three-pins-and-a-string-blob, three-ellipse, and three foci variant of Cassini oval.

Select an image, or take a photo if using mobile device. Move the image if needed. Choose p and q. Generate a tiling.

A draggable interactive hyperbolic tiling using the Poincare disc model.

Make successive zooms of the Mandelbrot set. The area picked is displayed in one canvas, the result is shown in another canvas.
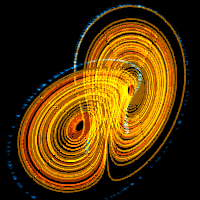
Interactive Lorenz attractor with 10,000 blue butterflies under the Lorenz attractor flow.

By using the points defining the squares of an animated Pythagoras' tree, it is possible to draw various paths to create a variety of animations.

A review of those properties of circle inversion that are needed in order to construct hyperbolic tools.

Raplaced the non-functional old GeoGebra applet with a Processing-version of the interactive Apollonian gasket.

I made a new section about non-Euclidean geometry. For now it's just an introduction.

Make a painting in Mondrian style. The painting is inverted in a circle as you paint.
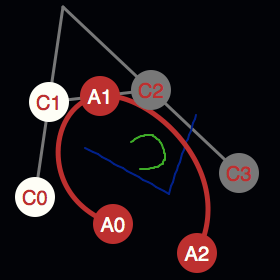
Splines are used to draw smooth curves. The construction of a cubic Bézier spline is explained and visualized.
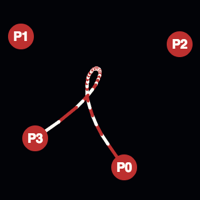
De Casteljau's algrithm is used to draw Beziér curves. Bézier curves are used when making smooth curves defined by points along a path.
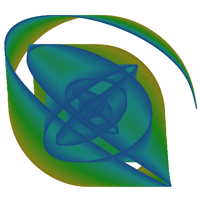
If two perpendicular pendulums are used to control the movement of a pen, the curve traced out is a so called damped Lissajous curve.

Imagine three coloured regions bordering to each other such that all three regions have exactly the same border!

The human brain uses shadows to interpret how objects move. By faking the shadow, one can fake the perceived motion of an object.
malin christersson on tumblr.
![]() 2019
2019