How to Make a Cubic Bézier Spline
| ←De Casteljau's Algorithm and Bézier Curves | Paint Circle-Inverted Mondrian!→ |
|---|
The continuity of a cubic Bézier spline
The red curve below is made by gluing together two cubic Bézier curves. The first Bézier curve is defined by the anchor points \(A_0, A_1\) and control points \(C_0, C_1\). The second is defined by anchor points \(A_1, A_2\) and control points \(C_2, C_3\).
An object \(s\) moving along the curve, has the velocity vector \(v\) and acceleration vector \(a\). These vectors can be placed anywhere. By placing them at a non-moving point, you can study the curves they trace out. The green curve is the curve of the velocity, and the blue curve is the curve of the acceleration.
A curve is continuous if you could draw it with a pen without lifting the pen from the paper. When measuring the smoothness of a curve, a curve is said to be \(C^0\) continuous if it is continuous. It is \(C^1\) continuous if both the curve and its velocity curve are continuous. It is \(C^2\) continuous if the curve itself, and the velocity curve, and the acceleration curve, are all continuous.
JavaScript is needed!
Move the points to make the blue curve continuous! (you probably ruin the continuity of the green curve)
Hide the velocity and acceleration vectors and show the mirror points!
When \(C_2\) lies on the grey mirror point \(C_1'\), the velocity is continuous.
When the yellow mirror points \(C_0'\) and \(C_3'\) coincide, the acceleration is continuous.
Lock \(C_2\) and \(C_3\) to an A-shape! Move the other points!
Calculus to explain the smoothness of A-shape
As was show on the previous page De Casteljau's Algorithm and Bézier Curves, the Bézier curves \(s_0(t)\) and \(s_1(t)\) are defined by:
\[ \begin{align*} s_0(t) &= (1-t)^3A_0+3(1-t)^2tC_0+3(1-t)t^2C_1+t^3A_1, t\in [0,1] \\ s_1(t) &= (1-t)^3A_1+3(1-t)^2tC_2+3(1-t)t^2C_3+t^3A_2, t\in [0,1]. \end{align*} \]Differentiating one time, we get the velocity curves \(v_0(t)\) and \(v_1(t)\):
\[ \begin{align*} v_0(t) &= 3 \left( (1-t)^2(C_0-A_0)+2(1-t)t(C_1-C_0)+t^2(A_1-C_1) \right), t\in [0,1] \\ v_1(t) &= 3 \left( (1-t)^2(C_2-A_1)+2(1-t)t(C_3-C_2)+t^2(A_2-C_3) \right), t\in [0,1]. \end{align*} \]Differentiating again, we get the acceleration curves \(a_0(t)\) and \(a_1(t)\):
\[ \begin{align*} a_0(t) &= 6\left( (1-t)(C_1-2C_0+A_0)+t(A_1-2C_1+C_0) \right), t\in [0,1] \\ a_1(t) &= 6\left( (1-t)(C_3-2C_2+A_1)+t(A_2-2C_3+C_2) \right), t\in [0,1]. \end{align*} \]In order for the velocity curve to be continuous, we must have that \(v_0(1)=v_1(0)\). In order for the acceleration curve to be continuous, we must have that \(a_0(1)=a_1(0)\). Hence we have two conditions
\[ \begin{align} A_1-C_1 &=C_2-A_1 \label{eq:one} \\ C_0-2C_1 &=C_3-2C_2 \label{eq:two}. \end{align} \]Showing the conditions geometrically
The conditions can be written using vectors.
Let \(O\) be the origin. A point \(A\) can be represented by its position vector \(\vec{OA}\), i.e. the vector having \(O\) as the start point and \(A\) as its terminal point. The first condition can now be written as
\[ \vec{OA_1}-\vec{OC_1} = \vec{OC_2}-\vec{OA_1}. \]By noting that \(\vec{OB}-\vec{OA} = \vec{AB} \) (see Linear Algebra - Vectors), the condition can be written as
\[ \vec{C_1A_1}=\vec{A_1C_2}. \]As for the second condition, it can be rewritten as
\[ 2C_1-C_0=2C_2-C_3 \Longleftrightarrow C_1+(C_1-C_0) = C_2+(C_2-C_3). \]Using vectors, we get that
\[ \vec{OC_1}+\vec{C_0C_1}=\vec{OC_2}+\vec{C_3C_2}. \]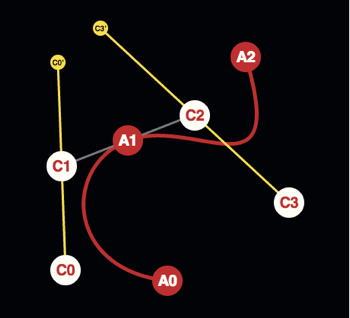
The velocity is continuous if \(C_2\) is the mirror point of \(C_1\) in \(A_1\).
The acceleration is continuous if the mirror point \(C_0'\) of \(C_0\) in \(C_1\), coincides with the mirror point \(C_3'\) of \(C_3\) in \(C_2\).
One way to make the red curve \(C^2\) continuous, is to let \(C_2\) be the mirror point of \(C_1\) in \(A_1\), and let \(C_3\) be the mirror point of \(C_0'\) in \(C_2\).
Another way to construct points on an A-shape is described next.
Making a \(C^2\) continuous cubic Bézier spline defined by points along a path
A spline is a piecewise defined function used for making a smooth curve defined by points along some path. In the example below, the yellow curve is a cubic Bézier spline defined by the red points.
JavaScript is needed!
In order to make a cubic Bézier spline, the control points and anchor points must be constructed. Let \(\left( P_i \right)_{i=1}^{n} \) be a sequence of \(n\) points (the red points in the example above).
When making an open spline, we need \(n\) anchor points and \(2(n-1)\) control points. In order to make points on A-shapes, make control points such that each pair of control points divide the corresponding line segment into three equal parts. As for the anchor points, let the first anchor point be \(P_1\) and the last anchor point \(P_n\). Let the other \(n-2\) anchor points be midpoints between control points as shown above.
When making a closed spine, we need \(n+1\) anchor points and \(2n\) control points. The control points are made as in the case of the open curve, but add a pair of control points between \(P_n\) and \(P_0\). The anchor points are midpoints between control points, as shown above. The first and last anchor points coincide.
In order to make a cubic Bézier spline where the anchor point are the same as the points \(\left( P_i \right)_{i=1}^{n} \), another method must be used. For more information see this pdf by Kirby A. Baker, Mathematics Department, UCLA.
In the demo below there is a delay to make the original strokes non-smooth.
JavaScript is needed!
The code
The processing-code to the examples can be seen here: Continuity of Bézier splines, Making a Bézier spline, Drawing a Bézier spline.
