Rolling Hypocycloids and Epicycloids
| ←Focal Points, Ellipses and Ovals | Möbius Transformation of a Doyle Spiral→ |
|---|
| Press a to make more shapes, or click on the icon. |
 |
| Press s to make fewer shapes, or click on the icon. |
 |
| Press w to change colours, or click on the icon. |
 |
| Move the mouse (or touch drag) to roll the shapes. | |
Explanation
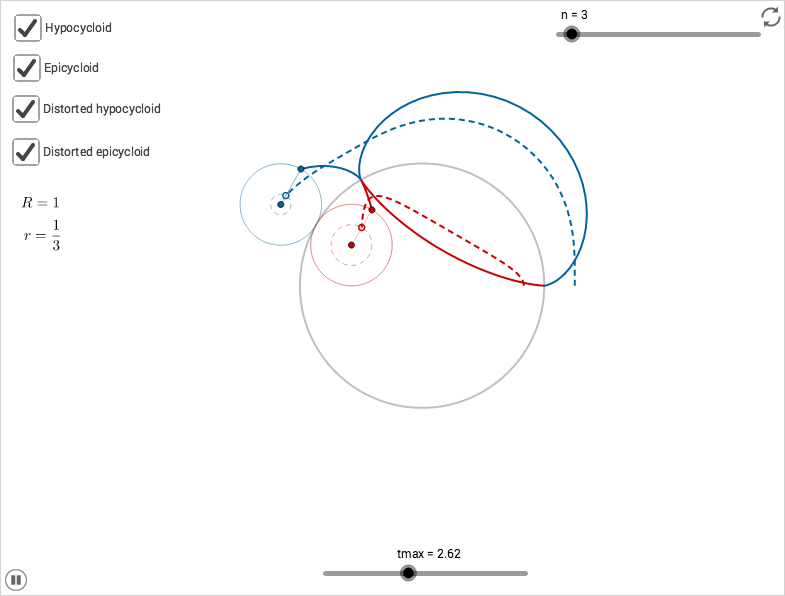
Hypocycloids and epicycloids are curves traced out by a point on a circle rolling on the inside or outside of another circle. These curves are special cases of hypotrochoids and epitrochoids (the cases when \(d=r\) using the notation from the side Make a Spirograph).
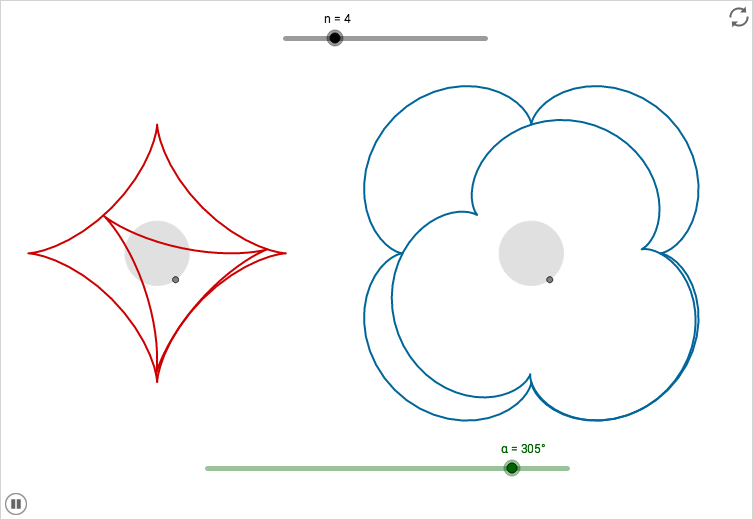
Let \(r\) be the radius of the rolling circle and \(R\) the radius of the fixed circle, then all curves having the same ratio \(R:r\) have the same shape. When the ratio \(R:r\) is an integer, as in the GeoGebra-example below, the curve traced out as the smaller circle rolls one revolution around the large circles is a closed curve. Furthermore, if the ratio is an integer \(n\) then the curves have \(n\) edges called cusps.
By letting the rolling circles have a smaller radius, thus smoothening the cusps, distorted versions of the curves are created
In the GeoGebra-example above, the equation for the hypocycloid is
\[ \begin{cases} x(t) = \dfrac{(n - 1) \cos(t) + \cos((n - 1) t)}{n} \\ y(t) = \dfrac{(n - 1) \sin(t) - \sin((n - 1) t)}{n} \end{cases} \]and for the epicycloid it is
\[ \begin{cases} x(t) = \dfrac{(n + 1) \cos(t) - \cos((n + 1) t)}{n} \\ y(t) = \dfrac{(n + 1) \sin(t) - \sin((n + 1) t)}{n}. \end{cases} \]Rolling on the inside
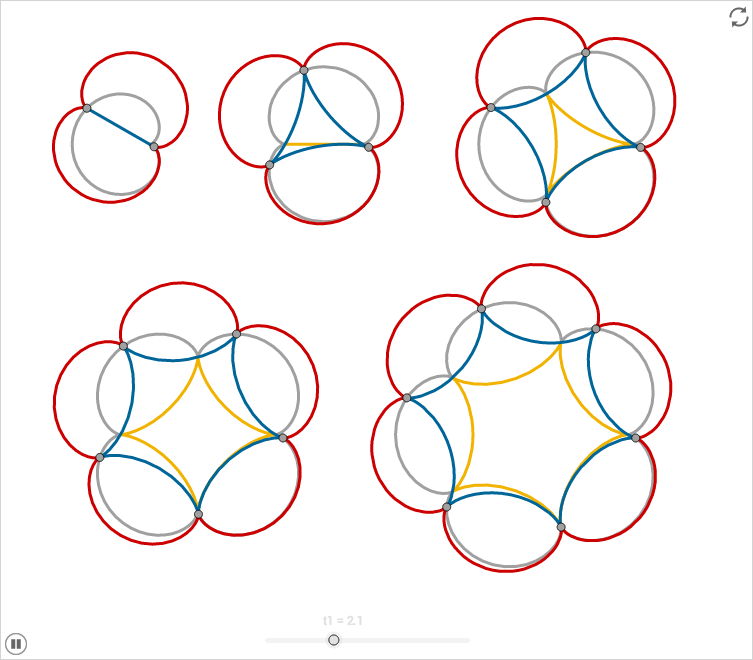
A hypocycloid (or epicycloid) with \(n\) cusps can move inside a hypocycloid (or epicycloid) with \(n+1\) cusps in such a way that the cusps of one of the curves always touches the other curve.
By repeating this pattern, examples such as the Javascript-examples above can be made.
Rolling on the outside
The cusps of a \((n+1)\)-hypocycloid, rolling on the outside of a \(n\)-hypocycloid, traces out a \(n\)-epicycloid.
Explanation:
If you roll a \(n\)-epicycloid on the inside of a \((n+1)\)-epicycloid,
the cusps of the outer epicycloid lie on the inner epicycloid. So if you instead roll epicycloids on the outside, the cusps of the \((n+1)\)-epicycloid (red below)
will glide along the inner \(n\)-epicycloid. Since the cusps of \((n+1)\)-epicycloids are the same points as the cusps of \((n+1)\)-hypocycloids,
we get that the cusps of a hypocycloid outlines an epicycloid when rolling on the outside.
Animated gifs
Distorted epicycloids and hypocycloids on tumblr.
Rolling epicycloids (black and white) on tumblr.
Rolling hypocycloids (black and white) on tumblr.
References
Ideas from the discussion by John Baez and others at: Azimuth - Rolling Hypocycloids.
GeoGebra-examples at geogebra.org: