The fifth postulate in Euclid's Elements can be rephrased as
The postulate is not true in 3D but in 2D it seems to be a valid statement. Considering the importance of postulates however, a seemingly valid statement is not good enough.

A postulate (or axiom) is a statement that acts as a starting point for a theory. Since a postulate is a starting point it cannot be proven using previous result. As a statement that cannot be proven, a postulate should be self-evident. The Elements of Euclid is built upon five postulates. For over 2000 years the fifth postulate has been considered to be less intuitive than the other postulates, and not sufficiently self-evident. Many attempts have been made to prove the fifth postulate using the other four postulates. All these attempts have failed. In the 19th century it was shown that the fifth postulate is independent of the other postulates. It is possible to build a theory of geometry where the fifth postulate is not true. Such geometries are called non-Euclidean. Furthermore, it can be shown that non-Euclidean theories can be just as consistent as Euclidean theory. A theory is consistent if it does not contain any contradiction.
The converse statement to the parallel postulate, as stated above, is that there are either no lines, or at least two lines "parallel to the given line through the point". It can be shown that if there is at least two lines, there are in fact infinitely many lines "parallel to...".
If the parallel postulate is replaced by:
you get an elliptic geometry.
If the parallel postulate is replaced by:
you get a hyperbolic geometry.

The theorems in the Elements of Euclid are built on a number of postulates and a number of definitions. Definition number 23 states that two lines are parallel if they never meet. There is nothing in the definition indicating that the distance between two parallel lines is the same everywhere. The parallel postulate is seemingly obvious only if you assume that parallel lines look like railroad tracks. If you redefine what you mean by a line, you may have that two parallel lines either converge towards each other or diverge from one another.
In non-Euclidean geometry, the concept corresponding to a line is a curve called a geodesic. In non-Euclidean geometry a shortest path between two points is along such a geodesic, or "non-Euclidean line".
All theorems in Euclidean geometry that use the fifth postulate, will be altered when you rephrase the parallel postulate. As an example; in Euclidean geometry the sum of the interior angles of a triangle is 180°, in non-Euclidean geometry this is not the case.
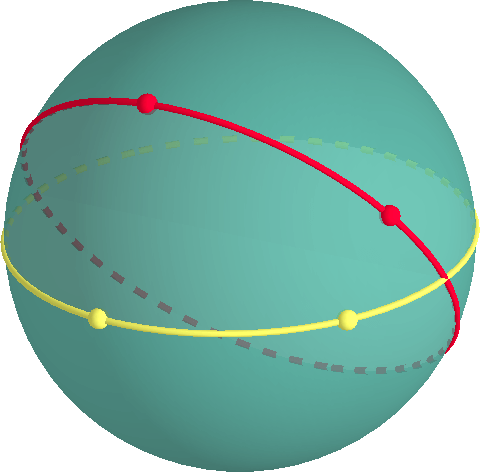
One easy way to model elliptical geometry is to consider the geometry on the surface of a sphere. A shortest path between two points on a sphere is along a so-called great circle. A great circle is a circle having the same radius, and the same centre, as the sphere. A great circle is a geodesic.
If two points are directly opposite each other on the sphere (like the north pole and south pole) there are infinitely many shortest paths between the points. If the points are not antipodes, there is only one shortest path.
Two great circles that are not the same, must intersect. Hence, there are no parallel lines on the surface of a sphere.
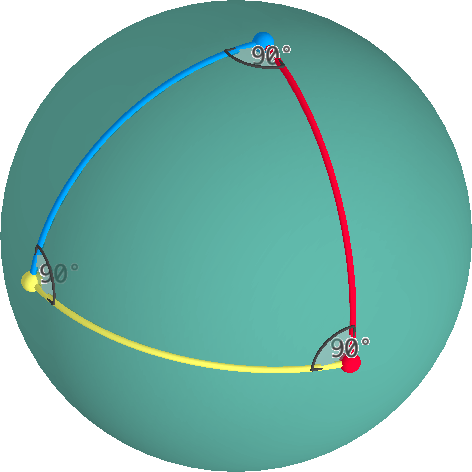
A triangle is defined by three vertices and three arcs along great circles through each pair of vertices.
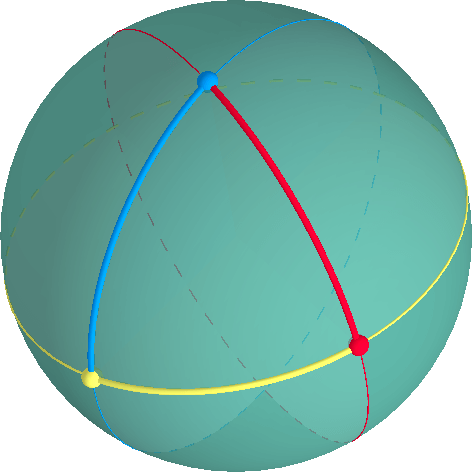
An interior angle at a vertex of a triangle can be measured on the tangent plane through that vertex. The sum of interior angles of an elliptical triangle is always > 180°.
The Poincaré disc (in 2D) is an open disc, i.e. a set of points bounded by a circle not including the circle. When using the Poincaré disc model, only points in the Poincaré disc are considered. The Poincaré disc makes up the entire world. The boundary of the open disc is the circle at infinity, \(C_\infty \).
A geodesic through points \(A\) and \(B\) is defined as the circular arc through \(A\) and \(B\) that is perpendicular to \(C_\infty \). If \(A\) and \(B\) lie on a diameter of \(C_\infty \), that diameter is the geodesic through \(A\) and \(B\).

An interior angle of a triangle is measured between the corresponding tangent lines. The sum of interior angles is always < 180°. If the vertices of a triangle move towards circle \(C_\infty \), the angle sum tend to 0. Points that lie at \(C_\infty \) are called ideal points. The limiting triangle as the vertices tend to infinity (\(C_\infty \)) is called an ideal triangle. An ideal triangle has angle sum 0. Since the vertices of an ideal triangle lie at infinity, the perimeter of an ideal triangle is infinite. Furthermore, it can be shown that the area of an ideal triangle is \(\pi\). Hence, all the triangles in the topmost animation have the same hyperbolic area.

A line divides a plane into two halves. When using the Poincaré halfplane model, only points in half of a plane (not including the line) are considered.
A geodesic through points \(A\) and \(B\) is defined as the circular arc through \(A\) and \(B\) that is perpendicular to the boundary line. If \(A\) and \(B\) lie on a line perpendicular to the boundary, a ray from the intersection point (not including the point) through \(A\) and \(B\) is the geodesic.

For non-Euclidean geometries all postulates in Euclid's Elements except the parallel postulate should be true. If you use geometry on a sphere to model elliptic geometry this is not the case (depending on how you interpret the first postulate). Use the Guide for Postulate 1 to explain why geometry on a sphere, as explained in the text, is not strictly non-Euclidean.
GeoGebra construction of elliptic geodesic.
Using GeoGebra show the 3D Graphics window! You can make spheres and planes by using commands or tools. To use a command start typing Sphere (or Plane) and GeoGebra will show you various alternatives for completing the code.
A circle on a sphere can be constructed by intersecting the sphere with a plane. You make an intersection by using the tool Intersect Two Surfaces. A great circle is constructed by choosing an appropriate plane to intersect the sphere with.
Make a sphere and put two points \(A\) and \(B\) on the sphere. Construct the geodesic through \(A\) and \(B\) by using an appropriate plane. Hide all auxiliary objects.
Measure an angle between two geodesics on a sphere using GeoGebra.
Put three points \(A\), \(B\) and \(C\) on a sphere and construct two geodesics that form the elliptic angle \( \angle ABC \). The angle is measured by using points on the plane through \(B\) tangent to the sphere. Construct the tangent plane. Construct two points on the plane that can be used to measure the angle. Measure the angle and hide all auxiliary objects.
Ideal triangles on Ello.