The Mandelbrot Set

Definition of the Mandelbrot set

Pick a complex number \(c\) and use the recursive formula

\[ \left\{ \begin{align*} z_0 &= c \\ z_{n+1} &= z_n^2+c, n \ge 0, \end{align*} \right. \]

if \( |z_n|\nrightarrow \infty \text{ as }n\rightarrow \infty \) then \(c\) belongs to the Mandelbrot set.

An escape-time fractal

It can be shown that if \(|z_n|>2\) for some \(n\), then \( |z_n|\to \infty \text{ as }n\rightarrow \infty \). When iterating the Mandelbrot set, it suffices to iterate as long as \(|z_n|^2\leq 4\), and as long as \(n\) is less than some fix maximum number of your own choice.

The points that belong to the Mandelbrot set are usually coloured black. The points that don't belong to the Mandelbrot set, will leave the circle with radius 2 for som integer \(n\), this \(n\) is called the escape-time. By letting each point get a colour that depends on its escape-time, you can make patterns that repeat themselves to infinity when zooming in. The repeating pattern is not exactly the same but almost. The black Mandelbrot blobs that keep appearing are similar to each other but they are all different.

Islands of Mandelbrot-blobs?

As long as you are in the vicinity of the Mandelbrot set when you zoom in, you will see new small islands, or blobs, looking like the original Mandelbrot set. Mandelbrot himself called them islands but they are actually not islands. It has been shown that all blobs are connected, the entire Mandelbrot set is a connected set. Because of the complexity you will never see the thin fractal paths connecting the blobs in a computer generated picture, regardless of how much you zoom. The only path that can be seen, is the negative \(x\)-axis (down to -2).

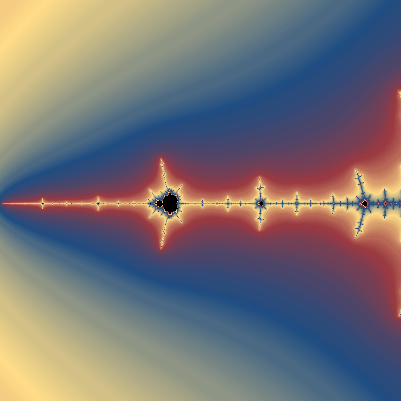
Colouring the points that don't belong to the Mandelbrot set

If the colour of a point depends linearly on its escape-time, there will be a multitude of colours very close to the Mandelbrot set. One way to get a more interesting fractal is to take the logarithm of the escape-time, thus making the fractal "less steep".

Since the escape-time is a step-function, the colouring of the points will have distinct steps. One way to get a smooth colouring is to use the algorithm described at Renormalizing the Mandelbrot Escape. In the canvases above, a variant of this algorithm is used on the zoomable canvases. As for the other two canvases (in each group), the left canvas is coloured using sine of the escape-time, and the right canvas is coloured using the argument of the complex number corresponding to each point at the escape-time.

References

About the connectedness of the Mandelbrot set: FAQ archive: The Mandelbrot set

jQuery Plugin used on this site for picking colours: Spectrum - The No Hassle jQuery Colorpicker